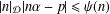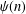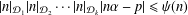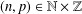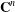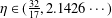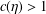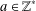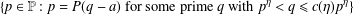Research Article
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
-
- Article
-
- You have access
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
-
- Article
-
- You have access
- Open access
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
-
- Article
-
- You have access
- Export citation
ON SOME NEW MOCK THETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 53-66
-
- Article
-
- You have access
- Export citation
CONTENT AND SINGLETONS BRING UNIQUE IDENTIFICATION MINORS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 67-90
-
- Article
-
- You have access
- Export citation
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 91-109
-
- Article
-
- You have access
- Export citation
TAME DISCRETE SUBSETS IN STEIN MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 110-132
-
- Article
-
- You have access
- Export citation
ON VALUES TAKEN BY THE LARGEST PRIME FACTOR OF SHIFTED PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2018, pp. 133-144
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
JAZ volume 107 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 July 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JAZ volume 107 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 July 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation