For any positive integer  n, let
n, let 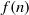 f(n) denote the number of solutions to the Diophantine equation
f(n) denote the number of solutions to the Diophantine equation
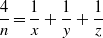 \begin{eqnarray*}\frac{4}{n} = \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\end{eqnarray*}
\begin{eqnarray*}\frac{4}{n} = \frac{1}{x} + \frac{1}{y} + \frac{1}{z}\end{eqnarray*}
with
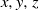 x, y, z
x, y, z positive integers. The
Erdős–Straus conjecture asserts that
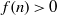 f(n)\gt 0
f(n)\gt 0 for every
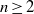 n\geq 2
n\geq 2. In this paper we obtain a number of upper and lower bounds for
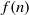 f(n)
f(n) or
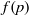 f(p)
f(p) for typical values of natural numbers
 n
n and primes
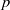 p
p. For instance, we establish that
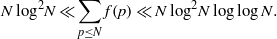 \begin{eqnarray*}N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\ll \displaystyle \sum _{p\leq N}f(p)\ll N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\log \log N.\end{eqnarray*}
\begin{eqnarray*}N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\ll \displaystyle \sum _{p\leq N}f(p)\ll N\hspace{0.167em} {\mathop{\log }\nolimits }^{2} N\log \log N.\end{eqnarray*}
These upper and lower bounds show that a typical prime has a small number of solutions to the Erdős–Straus Diophantine equation; small, when compared with other additive problems, like Waring’s problem.