Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T08:39:28.262Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNIVERSAL KUMMER CONGRUENCES

Part of: Elementary number theory Diophantine equations Sequences and sets

Published online by Cambridge University Press:  22 March 2013

SHAOFANG HONG ,
JIANRONG ZHAO  and
WEI ZHAO
SHAOFANG HONG*
Affiliation:
Yangtze Center of Mathematics, Sichuan University, Chengdu 610064, PR China Mathematical College, Sichuan University, Chengdu 610064, PR China
JIANRONG ZHAO
Affiliation:
School of Economic Mathematics, Southwestern University of Finance and Economics, Chengdu 610074, PR China email [email protected]
WEI ZHAO
Affiliation:
Science and Technology on Communication Security Laboratory, Chengdu 610041, PR China email [email protected]
*
✉[email protected][email protected][email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 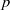$p$ be a prime. In this paper, we present a detailed 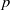$p$-adic analysis on factorials and double factorials and their congruences. We give good bounds for the 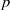$p$-adic sizes of the coefficients of the divided universal Bernoulli number 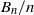${B}_{n} / n$ when $n$ is divisible by 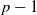$p- 1$. Using these, we then establish the universal Kummer congruences modulo powers of a prime 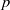$p$ for the divided universal Bernoulli numbers 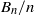${B}_{n} / n$ when $n$ is divisible by 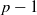$p- 1$.

Keywords

universal Bernoulli numberuniversal Kummer congruencedouble factorialp-adic valuationreduced partition

MSC classification

Secondary: 11D79: Congruences in many variables 11B68: Bernoulli and Euler numbers and polynomials 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 1 , February 2013 , pp. 106 - 132
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Adelberg, A., ‘Kummer congruences for universal Bernoulli numbers and related congruences for poly-Bernoulli numbers’, Int. Math. J. 1 (2002), 53–63.Google Scholar
Adelberg, A., ‘Universal Kummer congruences mod prime powers’, J. Number Theory 109 (2004), 362–378.CrossRefGoogle Scholar
Adelberg, A., Hong, S. and Ren, W., ‘Bounds of divided universal Bernoulli numbers and universal Kummer congruences’, Proc. Amer. Math. Soc. 136 (2008), 61–71.CrossRefGoogle Scholar
Baker, A., Clarke, F., Ray, N. and Schwartz, L., ‘On the Kummer congruences and the stable homotopy of BU’, Trans. Amer. Math. Soc. 316 (1989), 385–432.Google Scholar
Clarke, F., ‘The universal von Staudt theorem’, Trans. Amer. Math. Soc. 315 (1989), 591–603.CrossRefGoogle Scholar
Clarke, F. and Jones, C., ‘A congruence for factorials’, Bull. Lond. Math. Soc. 36 (2004), 553–558.CrossRefGoogle Scholar
Dibag, I., ‘An analogue of the von Staudt–Clausen theorem’, J. Algebra 87 (1984), 332–341.CrossRefGoogle Scholar
Glaisher, J. W. L., ‘On the residues of the sums of products of the first $p- 1$ numbers, and their powers, to modulus ${p}^{2} $ or ${p}^{3} $’, Quart. J. Pure Appl. Math. 31 (1900), 321–353.Google Scholar
Glaisher, J. W. L., ‘On the residues of the inverse powers of numbers in arithmetic progression’, Quart. J. Pure Appl. Math. 32 (1901), 271–305.Google Scholar
Hong, S., ‘Notes on Glaisher’s congruences’, Chinese Ann. Math. 21B (2000), 33–38.Google Scholar
Hurwitz, A., ‘Über die Entwicklungskoeffizienten der lemniskatischen Funktionen’, Math. Ann. 51 (1899), 196–226.CrossRefGoogle Scholar
Katz, N. M., ‘The congruences of Clausen–von Staudt and Kummer for Bernoulli–Hurwitz numbers’, Math. Ann. 216 (1975), 1–4.CrossRefGoogle Scholar
Koblitz, N., p-Adic Numbers, p-adic Analysis, and Zeta-functions, Graduate Texts in Mathematics, 58 (Springer, New York, 1984).CrossRefGoogle Scholar
Kummer, E. E., ‘Über eine allgemeine Eigenschaft der rationalen Entwicklungscoefficienten einer bestimmten Gattung analytischer Functionen’, J. reine angew. Math. 41 (1851), 368–372.Google Scholar
Lehmer, E., ‘On congruences involving Bernoulli numbers and the quotients of Fermat and Wilson’, Ann. of Math. (2) 39 (1938), 350–360.CrossRefGoogle Scholar
Miller, H., Universal Bernoulli numbers and the S 1-transfer, Canadian Mathematical Society Conference Proceedings, 2 (American Mathematical Society, Providence, RI, 1982), 437–449.Google Scholar
Murty, M. R., Introduction to p-adic Analytic Number Theory, Studies in Advanced Mathematics, 27 (American Math. Soc, Providence, RI, 2002).Google Scholar
Ray, N., ‘Extensions of umbral calculus I: Penumbral coalgebras and generalised Bernoulli numbers’, Adv. Math. 61 (1986), 41–100.CrossRefGoogle Scholar
Robert, A., A Course in p-adic Analysis, Graduate Texts in Mathematics, 198 (Springer, New York, 2000).CrossRefGoogle Scholar
Tempesta, P., ‘Formal groups, Bernoulli-type polynomials and L-series’, C. R. Acad. Paris, Ser. I 345 (2007), 303–306.CrossRefGoogle Scholar
Young, P. T., ‘Congruences for Bernoulli, Euler and Stirling numbers’, J. Number Theory 78 (1999), 204–227.CrossRefGoogle Scholar
Young, P. T., ‘Kummer congruences for values of Bernoulli and Euler polynomials’, Acta Arith. 99 (2001), 277–288.CrossRefGoogle Scholar
Zhao, J., ‘Wolstenholme type theorem for multiple harmonic sums’, Int. J. Number Theory 4 (2008), 73–106.CrossRefGoogle Scholar