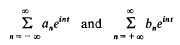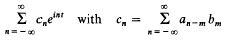Research Article
The SQ-universality of some finitely presented groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
A construction of rings whose injective hulls allow a ring structure
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-13
-
- Article
-
- You have access
- Export citation
Negative curvature and combinatorial group theory
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 14-15
-
- Article
-
- You have access
- Export citation
Isomorphisms induced by automorphisms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-17
-
- Article
-
- You have access
- Export citation
The third term of the lower central series of a free group as a subgroup of the second
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-23
-
- Article
-
- You have access
- Export citation
The simple groups related to M24, II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 24-28
-
- Article
-
- You have access
- Export citation
Some infinitely based varieties of groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-32
-
- Article
-
- You have access
- Export citation
Groups with an automorphism squaring many elements
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-42
-
- Article
-
- You have access
- Export citation
Lattice automorphisms of semi-simple Lie algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 43-53
-
- Article
-
- You have access
- Export citation
The path functor and faithful representability of banach lie algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 54-69
-
- Article
-
- You have access
- Export citation
Formal multiplication of trigonometric series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 70-77
-
- Article
-
- You have access
- Export citation
On minimal irregular p-Groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 78-89
-
- Article
-
- You have access
- Export citation
Permutable subgroups of some finite p-groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-97
-
- Article
-
- You have access
- Export citation
Subgroups of finitely presented metabelian groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 98-110
-
- Article
-
- You have access
- Export citation
Alternating trilinear forms and groups of exponent 6
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-128
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 16 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 16 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation