Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T01:18:20.890Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGICAL FULL GROUPS OF 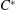$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM 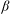$\beta $-EXPANSIONS

Part of: Structure and classification of infinite or finite groups Ergodic theory Topological dynamics

Published online by Cambridge University Press:  17 July 2014

KENGO MATSUMOTO  and
HIROKI MATUI
KENGO MATSUMOTO*
Affiliation:
Department of Mathematics, Joetsu University of Education, Joetsu 943-8512, Japan email [email protected]
HIROKI MATUI
Affiliation:
Graduate School of Science, Chiba University, Inage-ku, Chiba 263-8522, Japan
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce a family of infinite nonamenable discrete groups as an interpolation of the Higman–Thompson groups by using the topological full groups of the groupoids defined by 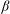$\beta $-expansions of real numbers. They are regarded as full groups of certain interpolated Cuntz algebras, and realized as groups of piecewise-linear functions on the unit interval in the real line if the 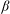$\beta $-expansion of 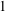$1$ is finite or ultimately periodic. We also classify them by a number-theoretical property of 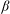$\beta $.

Keywords

Cuntz algebrasC∗-algebrasHigman–Thompson groupsβ-expansionfull groupssymbolic dynamics

MSC classification

Secondary: 20E32: Simple groups 37A45: Relations with number theory and harmonic analysis 37A55: Relations with the theory of $C^*$-algebras 37B10: Symbolic dynamics
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 2 , October 2014 , pp. 257 - 287
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bertrand-Mathis, A., ‘Développement en base θ, répartition modulo un de la suite (x θ n)n≥0, languages codés et θ-shift’, Bull. Soc. Math. France 114 (1986), 271–323.Google Scholar
Blanchard, F., ‘β-expansions and symbolic dynamics’, Theoret. Comput. Sci. 65 (1989), 131–141.Google Scholar
Brown, K. S., ‘Finiteness properties of groups’, J. Pure Appl. Algebra 44 (1987), 45–75.Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R., ‘Introductory notes on Richard Thompson’s groups’, Enseign. Math. 42(2) (1996), 215–256.Google Scholar
Cleary, S., ‘Regular subdivision in ℤ[(1 +√ 5)∕2]’, Illinois J. Math. 44 (2000), 453–464.Google Scholar
Crainic, M. and Moerdijk, I., ‘A homology theory for étale groupoids’, J. reine angew. Math. 521 (2000), 25–46.Google Scholar
Cuntz, J., ‘Simple C ∗-algebras generated by isometries’, Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
Cuntz, J., ‘K-theory for certain C ∗-algebras’, Ann. of Math. (2) 113 (1981), 181–197.Google Scholar
Cuntz, J. and Krieger, W., ‘A class of C ∗-algebras and topological Markov chains’, Invent. Math. 56 (1980), 251–268.Google Scholar
Deaconu, V., ‘Groupoids associated with endomorphisms’, Trans. Amer. Math. Soc. 347 (1995), 1779–1786.Google Scholar
Frougny, C. and Solomyak, B., ‘Finite β-expansions’, Ergodic Theory Dynam. Systems 12 (1992), 713–723.Google Scholar
Higman, G., ‘Finitely presented infinite simple groups’, Notes on Pure Mathematics, Vol. 8 (Australian National University, Canberra, 1974).Google Scholar
Katayama, Y., Matsumoto, K. and Watatani, Y., ‘Simple C ∗-algebras arising from β-expansion of real numbers’, Ergodic Theory Dynam. Systems 18 (1998), 937–962.CrossRefGoogle Scholar
Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding (Cambridge University Press, Cambridge, 1995).Google Scholar
Matsumoto, K., ‘C ∗-algebras associated with presentations of subshifts’, Doc. Math. 7 (2002), 1–30.Google Scholar
Matsumoto, K., ‘Orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras’, Pacific J. Math. 246 (2010), 199–225.Google Scholar
Matsumoto, K., ‘Classification of Cuntz–Krieger algebras by orbit equivalence of topological Markov shifts’, Proc. Amer. Math. Soc. 141 (2013), 2329–2342.Google Scholar
Matsumoto, K., ‘K-groups of the full group actions on one-sided topological Markov shifts’, Discrete Contin. Dyn. Syst. 33 (2013), 3753–3765.Google Scholar
Matsumoto, K., Full groups of one-sided topological Markov shifts, Israel J. Math., to appear.Google Scholar
Matsumoto, K. and Matui, H., Continuous orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras, Kyoto J. Math., to appear.Google Scholar
Matui, H., ‘Some remarks on topological full groups of Cantor minimal systems’, Internat. J. Math. 17 (2006), 231–251.Google Scholar
Matui, H., ‘Homology and topological full groups of étale groupoids on totally disconnected spaces’, Proc. Lond. Math. Soc. 104 (2012), 27–56.Google Scholar
Matui, H., ‘Some remarks on topological full groups of Cantor minimal systems II’, Ergodic Theory Dynam. Systems 33 (2013), 1542–1549.Google Scholar
Matui, H., Topological full groups of one-sided shifts of finite type, J. reine angew Math., to appear.Google Scholar
Nekrashevych, V. V., ‘Cuntz–Pimsner algebras of group actions’, J. Operator Theory 52 (2004), 223–249.Google Scholar
Pardo, E., ‘The isomorphism problem for Higman–Thompson groups’, J. Algebra 344 (2011), 172–183.Google Scholar
Parry, W., ‘On the β-expansion of real numbers’, Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Renault, J., A Groupod Approach to C ∗-Algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin–Heidelberg–New York, 1980).Google Scholar
Renault, J., ‘Cartan subalgebras in C ∗-algebras’, Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Rényi, A., ‘Representations for real numbers and their ergodic properties’, Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.Google Scholar
Rørdam, M., ‘Classification of Cuntz–Krieger algebras’, K-Theory 9 (1995), 31–58.Google Scholar
Thompson, R. J., ‘Embeddings into finitely generated simple groups which preserve the word problem’, in: Word Problems II, Studies in Logic and the Foundations of Mathematics, 95 (eds. Adian, S. I., Boone, W. W. and Higman, G.) (North-Holland, Amsterdam, 1980), 401–441.Google Scholar