Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T19:55:35.425Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on partitions

Published online by Cambridge University Press:  09 April 2009

R. L. Graham
R. L. Graham
Affiliation:
Bell Telephone Laboratories, Inc., Murray Hill, New Jersey.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

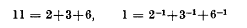Certain integers have the property that they can be partitioned into distinct positive integers whose reciprocals sum to 1, e.g., and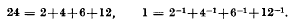 In this paper we prove that all integers exceeding 77 possess this property. This result can then be used to establish the more general theorem that for any positive rational numbers α and β there exists an integer r(α, β) such that any integer exceeding r(α, β) can be partitioned into distinct positive integers exceeding β whose reciprocals sum to α.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 4 , November 1963 , pp. 435 - 441
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Graham, R., On Finite Sums of Unit Fractions, (to appear in Proc.London Math. Soc.).Google Scholar
[2]Lev`que, W., Topics in Number Thory (Addison-Wesley, Reading, 1956), p. 76.Google Scholar