Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:16:22.207Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLE AND SEMISTABLE PROBABILITY MEASURES ON CONVEX CONE

Part of: Probability theory on algebraic and topological structures Distribution theory - Probability

Published online by Cambridge University Press:  20 November 2014

NAM BUI QUANG  and
PHUC HO DANG
NAM BUI QUANG
Affiliation:
Academy of Antiaircraft and Air Forces, Son Tay Town, Ha Noi, Vietnam email [email protected]
PHUC HO DANG*
Affiliation:
Institute of Mathematics, VAST, 18 Hoang Quoc Viet, Ha Noi, Vietnam email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The study concerns semistability and stability of probability measures on a convex cone, showing that the set 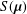$S(\boldsymbol{{\it\mu}})$ of all positive numbers 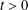$t>0$ such that a given probability measure 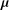$\boldsymbol{{\it\mu}}$ is $t$-semistable establishes a closed subgroup of the multiplicative group 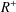$R^{+}$; semistability and stability exponents of probability measures are positive numbers if and only if the neutral element of the convex cone coincides with the origin; a probability measure is (semi)stable if and only if its domain of (semi-)attraction is not empty; and the domain of attraction of a given stable probability measure coincides with its domain of semi-attraction.

Keywords

convex cone(semi)stable probability measures(semi)stability exponentdomain of (semi-)attraction

MSC classification

Primary: 60E07: Infinitely divisible distributions; stable distributions
Secondary: 60B12: Limit theorems for vector-valued random variables (infinite-dimensional case)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 390 - 406
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Adler, R. J., Feldman, R. E. and Taqqu, M. S., A Practical Guide to Heavy Tailed Data (Birkhäuser, Boston, MA, 1998).Google Scholar
Berg, C., Christensen, J. P. R. and Ressel, P., Harmonic Analysis on Semigroups (Springer, Berlin, 1984).Google Scholar
Billingsley, P., Convergence of Probability Measures (John Wiley, New York, 1999).Google Scholar
Chorny, V., ‘Operator-semistable distributions on R d ’, Teor. Veroyatn. Primen. 31 (1986), 795–797; translation in Theory Probab. Appl. 31 (1986), 703–705.Google Scholar
Chung, D. M., ‘Characterizations of r-semistable probability measures on Hilbert spaces’, J. Korean Math. Soc. 17(1) (1980), 153–160.Google Scholar
Davydov, Y., Molchanov, I. and Zuyev, S., ‘Strictly stable distributions on convex cones’, Electron. J. Probab. 13 (2008), 259–321.CrossRefGoogle Scholar
Fama, E., ‘The behavior of stock prices’, J. Bus. 38 (1965), 34–105.Google Scholar
Giné, E. and Hahn, M. G., ‘Characterization and domains of attraction of p-stable compact sets’, Ann. Probab. 13 (1985), 447–468.Google Scholar
Gnedenko, B. V. and Kolmogorov, A. N., Limit Distributions for Sum of Independent Random Variables (Addison-Wesley, Reading, MA, 1954).Google Scholar
Gyeong, S. C., ‘Characterization of strictly operator semi-stable distributions’, J. Korean Math. Soc. 38(1) (2001), 101–123.Google Scholar
Hazod, W., ‘Stable probability measures on groups and on vector spaces’, in: Probability Measures on Groups VIII, Lecture Notes in Mathematics, 1210 (Springer, Berlin, 1986), 304–352.CrossRefGoogle Scholar
Hazod, W. and Siebert, P., Stable Probability Measures on Euclidean Spaces and on Locally Compact Groups (Kluwer, Dordrecht, 2001).CrossRefGoogle Scholar
Huillet, T., Porzio, A. and Benalaya, M., ‘On Lévy stable and semistable distributions’, Fractals 9(3) (2001), 347–364.Google Scholar
Jajte, R., ‘On stable distributions in Hilbert space’, Studia Math. 30 (1964), 63–71.CrossRefGoogle Scholar
Jajte, R., ‘Semistable probability measures on R N ’, Studia Math. 61 (1977), 29–39.CrossRefGoogle Scholar
Jurek, Z. J., ‘On Gaussian measures on $R^{d}$ ’, Proc. Sixth Conf. Probability Theory, Brasov, Romania, 1979 (Academy of Science of Romania, Bucharest, 1981), 313–316.Google Scholar
Jurek, Z. J., ‘Domain of normal attraction of operator stable measures on Euclidean spaces’, Bull. Pol. Acad. Sci. Math. Astron. Phys. 28(7–8) (1980), 397–401.Google Scholar
Kelley, J. L. and Namioka, I., Linear Topological Spaces (Van Nostrand, Princeton, NJ, 1963).CrossRefGoogle Scholar
Kotz, S., Kozubowski, T. J. and Podgórski, K., The Laplace Distributions and Generalizations (Birkhäuser, Boston, MA, 2001).Google Scholar
Kruglov, V. M., ‘On the extension of the class of stable distributions’, Teor. Veroyatn. Primen. 17 (1972), 723–732 (in Russian); translation in Theory Probab. Appl. 17 (1972), 685–694.Google Scholar
Kumar, A., ‘Semi-stable probability measures on Hilbert spaces’, J. Multivariate Anal. 6 (1976), 309–318.CrossRefGoogle Scholar
Kumar, A. and Mandrenkar, V., ‘Stable probability measures on Banach spaces’, Studia Math. 42 (1972), 133–144.Google Scholar
Kunst, R. M., ‘Apparently stable increments in finance data: could ARCH effects be the cause?’, J. Stat. Comput. Simul. 45 (1993), 121–127.CrossRefGoogle Scholar
Lévy, P., Théorie de l’addition des variables aléatoires (Gauthier-Villars, Paris, 1937).Google Scholar
Linde, W. and Siegel, G., ‘On the convergence of types for Radon probability measures in Banach spaces’, Proc. Probability in Banach Spaces IV, 6, Sandbjerg, Denmark, 1986, Progress in Probability, 20 (Birkhäuser, Boston, MA, 1990), 234–251.Google Scholar
Luczak, A., ‘Elliptical symmetry and characterization of operator stable and operator semistable probability measures’, Ann. Probab. 12(4) (1984), 1217–1223.Google Scholar
Mandelbrot, B., ‘The variation of certain speculative prices’, J. Bus. 37 (1963), 394–419.CrossRefGoogle Scholar
McCulloch, J., ‘Financial applications of stable distributions’, in: Handbook of Statistics, Vol. 14 (eds. Maddala, G. and Rao, C.) (Elsevier Science/North-Holland, Amsterdam, 1996), 393–425.Google Scholar
Palmer, K. J., Ridout, M. S. and Morgan, B. J. T., ‘Modelling cell generation times using the tempered stable distribution’, J. R. Stat. Soc. Ser. C 57 (2008), 379–397.Google Scholar
Parthasarathy, K. R., Probability Measures on Metric Spaces (Academic Press, New York, London, 1967).CrossRefGoogle Scholar
Samorodnitsky, G. and Taqqu, M. S., Stable Non-Gaussian Random Processes (Chapman and Hall, London, 1994).Google Scholar
Samuelson, P., ‘Eficient portfolio selection for Pareto–Lévy investments’, J. Financ. Quant. Anal. 2 (1967), 107–117.Google Scholar
Sato, K., ‘Strictly operator-stable distributions’, J. Multivariate Anal. 22 (1987), 278–295.Google Scholar
Sato, K., Lévy Processes and Infinitely Divisible Distributions (Cambridge University Press, Cambridge, UK, 1999).Google Scholar
Siegel, G., ‘Operator-stable distributions in separable Banach spaces’, Teor. Veroyatn. Primen. 34(3) (1989), 552–560; translation in Theory Probab. Appl. 34(3) (1989), 497–505.Google Scholar
Vakhaniya, N. N., Tarieladze, V. and Tchobanyan, S. A., Probability Distributions in Banach Spaces (Nauka, Moscow, 1985) (in Russian).Google Scholar
Zolotarev, V. M., One-Dimensional Stable Distributions, Translations of Mathematical Monographs, 65 (American Mathematical Society, Providence, RI, 1986).Google Scholar