Article contents
SOBOLEV SPACES ON LOCALLY COMPACT ABELIAN GROUPS AND THE BOSONIC STRING EQUATION
Published online by Cambridge University Press: 14 October 2014
Abstract
Motivated by a class of nonlinear nonlocal equations of interest for string theory, we introduce Sobolev spaces on arbitrary locally compact abelian groups and we examine some of their properties. Specifically, we focus on analogs of the Sobolev embedding and Rellich–Kondrachov compactness theorems. As an application, we prove the existence of continuous solutions to a generalized bosonic string equation posed on an arbitrary compact abelian group, and we also remark that our approach allows us to solve very general linear equations in a 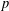 $p$-adic context.
$p$-adic context.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by


