Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T09:19:11.486Z Has data issue: false hasContentIssue false
  • English
  • Français

RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES

Part of: Computational aspects Diophantine approximation, transcendental number theory Zeta and $L$-functions: analytic theory Sequences and sets

Published online by Cambridge University Press:  15 June 2012

KH. HESSAMI PILEHROOD  and
T. HESSAMI PILEHROOD
KH. HESSAMI PILEHROOD
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova Scotia, Canada B3H 3J5 (email: [email protected])
T. HESSAMI PILEHROOD*
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova Scotia, Canada B3H 3J5 (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we present new explicit simultaneous rational approximations which converge subexponentially to the values of the Bell polynomials at the points 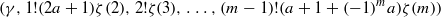where m=1,2,…,a, a∈ℕ, γ is Euler’s constant and ζ is the Riemann zeta function.

Keywords

Euler constantzeta valueBell polynomialBernoulli polynomialMeijer G-functionrational approximationsaddle point method

MSC classification

Secondary: 11J13: Simultaneous homogeneous approximation, linear forms 11B68: Bernoulli and Euler numbers and polynomials 11M35: Hurwitz and Lerch zeta functions 33F10: Symbolic computation (Gosper and Zeilberger algorithms, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 92 , Issue 1 , February 2012 , pp. 71 - 98
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2012

Footnotes

This research was in part supported by grants no. 89110024 (first author) and no. 89110025 (second author) from the School of Mathematics, Institute for Research in Fundamental Sciences (IPM).

References

[1]Aptekarev (ed.), A. I., Rational Approximation of Euler’s Constant and Recurrence Relations, Current Problems in Math., 9 (Steklov Math. Inst. RAS, Moscow, 2007).Google Scholar
[2]Bell, E. T., ‘Exponential polynomials’, Ann. of Math. (2) 35 (1934), 258–277.CrossRefGoogle Scholar
[3]Comtet, L., Advanced Combinatorics (D. Reidel, Dordrecht, 1974).Google Scholar
[4]de Bruijn, N. G., Asymptotic Methods in Analysis (Dover, New York, 1981).Google Scholar
[5]Fedoryuk, M. V., Asymptotics: Integrals and Series, Mathematical Reference Library (Nauka, Moscow, 1987).Google Scholar
[6]Hessami Pilehrood, Kh. and Hessami Pilehrood, T., ‘On a continued fraction expansion for Euler’s constant’, Preprint, arXiv:1010.1420[math.NT].Google Scholar
[7]Hessami Pilehrood, Kh. and Hessami Pilehrood, T., ‘Rational approximations for the quotient of Gamma values’, Indag. Math. 20(4) (2009), 583–601.CrossRefGoogle Scholar
[8]Hessami Pilehrood, Kh. and Hessami Pilehrood, T., ‘Rational approximations for values of the digamma function and a conjecture on denominators’, Mat. Zametki 90(5) (2011), 744–763. English transl.: Math. Notes 90(5) (2011), 730–747.Google Scholar
[9]Luke, Y. L., The Special Functions and Their Approximations, Vol. 1 (Academic Press, New York, 1969).Google Scholar
[10]Nörlund, N. E., ‘‘Mémoire sur les polynomes de Bernoulli’, Acta Math. 43 (1922), 121–196.CrossRefGoogle Scholar
[11]Petkovšek, M., Wilf, H. S. and Zeilberger, D., A=B (A. K. Peters, Wellesley, MA, 1997).Google Scholar
[12]Rivoal, T., ‘Rational approximations for values of derivatives of the Gamma function’, Trans. Amer. Math. Soc. 361 (2009), 6115–6149.CrossRefGoogle Scholar
[13]Tulyakov, D. N., ‘A system of recurrence relations for rational approximations of the Euler constant’, Math. Notes 85(5) (2009), 746–750.CrossRefGoogle Scholar