Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T20:36:57.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal natural dualities: the role of endomorphisms

Part of: Boolean algebras (Boolean rings) Other classes of algebra Distributive lattices

Published online by Cambridge University Press:  09 April 2009

M. J. Saramago
M. J. Saramago
Affiliation:
Departmento de Matemática, Faculdade de Ciências, Universidade de Lisboa, 1749–016 Lisboa, Portugal e-mail: [email protected] Centro de Álgebra, Universidade de Lisboa, Av. Prof. Gama Pinto 2, 1649–003 Lisboa, Portugal
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The optimality of dualities on a quasivariety 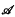, generated by a finite algebra 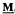, has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on 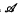, an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when 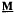is a subdirectly irreducible lattice-structured algebra.

Keywords

natural dualityoptimal dualityfailset

MSC classification

Secondary: 06D05: Structure and representation theory 06D30: De Morgan algebras, L ukasiewicz algebras 08C15: Quasivarieties
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 77 , Issue 2 , October 2004 , pp. 269 - 296
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Clark, D. M. and Davey, B. A., Natural dualities for the working algebraist (Cambridge University Press, Cambridge, 1998).Google Scholar
[2]Davey, B. A., Haviar, M. and Priestley, H. A., ‘The syntax and semantics of entailment in duality theory’, J. Symbolic Logic 60 (1995), 1087–1114.CrossRefGoogle Scholar
[3]Davey, B. A. and Priestley, H. A., ‘Optimal natural dualities’, Trans. Amer. Math. Soc. 338 (1993), 655–677.CrossRefGoogle Scholar
[4]Davey, B. A. and Priestley, H. A., ‘Optimal natural dualities II: general theory’, Trans. Amer. Math. Soc. 348 (1996), 3673–3711.CrossRefGoogle Scholar
[5]Davey, B. A. and Werner, H., ‘Dualities and equivalences for varieties of algebras’, in: Contributions to lattice theory (Szeged, 1980) (eds. Huhn, A. P. and Schmidt, E. T.), Colloq. Math. Soc. János Bolyai 33 (North-Holland, Amsterdam, 1983) pp. 101–275.Google Scholar
[6]Saramago, M. J., ‘A note on the covers of congruences of a finite lattice-structured algebra’, preprint.Google Scholar
[7]Saramago, M. J., ‘Optimal natural dualities for some quasivarieties of distributive double p-algebras’, Acta Math. Univ. Comenian. (N.S.) 67 (1998), 249–271.Google Scholar
[8]Saramago, M. J., A study of natural dualities, including an analysis of the structure of failsets (Ph.D. Thesis, Universidade de Lisboa, Portugal, 1999).Google Scholar
[9]Saramago, M. J. and Priestley, H. A., ‘Optimal natural dualities: the structure of failsets’, Internat. J. Algebra Comput. 12 (2002), 407–436.CrossRefGoogle Scholar
[10]Wegener, C., Natural dualities for varieties generated by lattice-structured algebras (Ph.D. Thesis, University of Oxford, 1999).Google Scholar