Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T08:43:01.478Z Has data issue: false hasContentIssue false
  • English
  • Français

On the differential equations of H. Lewy

Published online by Cambridge University Press:  09 April 2009

W. B. Smith-White
W. B. Smith-White
Affiliation:
University of Sydney.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that the theory of Cauchy's problem for differential equations with two independent variables is réducible to the corresponding problem for systems of quasi-linear equations. The reduction is carried further, by means of the theory of characteristics, to the case of systems of equations of the special form first considered by H. Lewy [1]. The simplest case is that of the pair of equations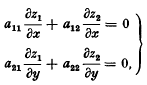where the aii depend on z1 and z2. The problem to be considered is that of finding functions z1(x, y), z2(x, y) which satisfy (1) and which take prescribed values on x + y = 0.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 2 , Issue 1 , April 1961 , pp. 11 - 16
Copyright
Copyright © Australian Mathematical Society 1961

References

[1]Lewy, H.: Math. Ann. Band 98, 1927.Google Scholar
[2]Courant, u. Hilbert: Methoden der mathematischen Physik, Band II, Kap. 5. Berlin: Springer 1937.Google Scholar
[3]Sauer, R.: Anfangswertprobleme bei partiellen Differenzialgleichungen, Kap. 3. Berlin: Springer 1958.CrossRefGoogle Scholar