Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T20:12:02.940Z Has data issue: false hasContentIssue false
  • English
  • Français

On closure and factorization properties of subexponential and related distributions

Part of: Distribution theory - Probability Limit theorems

Published online by Cambridge University Press:  09 April 2009

Paul Embrechts  and
Charles M. Goldie
Paul Embrechts
Affiliation:
Department Wiskunde Katholieke Universiteit LeuvenCelestijnenlaan 200B, B-3030 Heverlee Belgium
Charles M. Goldie
Affiliation:
Department of Mathematics Westfield College University of LondonKidderpore Avenue London NW3 7ST, United Kingdom
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

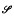For a distribution function F on [0, ∞] we say F ∈ if {1 – F(2)(x)}/{1 – F(x)}→2 as x→∞, and F∈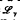, if for some fixed γ > 0, and for each real 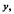, limx→∞ {1 – F(x + y)}/{1 – F(x)} ═ e– n. Sufficient conditions are given for the statement F ∈ 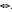F * G ∈ 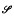and when both F and G are in y it is proved that F*G∈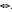pF + 1(1 – p) G ∈ for some (all) p ∈(0,1). The related classes ℒt are proved closed under convolutions, which implies the closure of the class of positive random variables with regularly varying tails under multiplication (of random variables). An example is given that shows 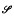to be a proper subclass of ℒ 0.

MSC classification

Secondary: 60E05: Distributions 60F99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 29 , Issue 2 , March 1980 , pp. 243 - 256
Copyright
Copyright © Australian Mathematical Society 1980

References

Bingham, N. H. and Teugels, J. L. (1979), ‘Tauberian theorems and regular variation’, Nieuw Arch. Wisk. (3) 27, 153–186.Google Scholar
Breiman, L. (1965), ‘On some limit theorems similar to the arc-sin law’, Theor. Probability Appl. 10, 323–331.CrossRefGoogle Scholar
Chistyakov, V. P (1964), ‘A theorem on sums of independent, positive random variables and its applications to branching processes’, Theor. Probability Appl. 9, 640–648.CrossRefGoogle Scholar
Chover, J., Ney, P. and Wainger, S. (1973), ‘Degeneracy properties of subcritical branching processes’, Ann. Probability 1, 663–673.Google Scholar
Embrechts, P., Goldie, C. M. and Veraverbeke, N. (1979), ‘Subexponentiality and infinite divisibility’, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete. 49, 335–347.Google Scholar
Goldie, C. M. (1978), ‘Subexponential distributions and dominated-variation tails’, J. Appl. Prob. 15, 440–442.CrossRefGoogle Scholar
Pitman, E. J. G. (1979), ‘Subexponential distribution functions’ (Personal communication).Google Scholar