Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T08:53:10.606Z Has data issue: false hasContentIssue false
  • English
  • Français

A limit theorem for Markov chains with continuous state space

Published online by Cambridge University Press:  09 April 2009

P. D. Finch
P. D. Finch
Affiliation:
University of Melbourne.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R denote the set of real numbers, B the σ-field of all Borel subsets of R. A homogeneous Markov Chain with state space a Borel subset Ω of R is a sequence {an}, n≧ 0, of random variables, taking values in Ω, with one-step transition probabilities P(1) (ξ, A) defined by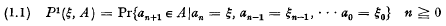 for each choice of ξ, ξ0, …, ξn−1 in ω and all Borel subsets A of ω The fact that the right-hand side of (1.1) does not depend on the ξi, 0 ≧ i > n, is of course the Markovian property, the non-dependence on n is the homogeneity of the chain.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 3 , August 1963 , pp. 351 - 358
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Doob, J. L., Stochastic Processes. (John Wiley, 1953).Google Scholar
[2]Finch, P. D., Storage problems along a production line of Continuous Flow. Ann. Univ. Sci. Bud. III–IV, 67–84 (1960/1961).Google Scholar
[3]Finch, P. D., Deterministic Customer Impatience in the queueing system GI/M/1. Biometrika, 47, 45–52 (1960).Google Scholar
[4]Finch, P. D., Deterministic Customer Impatience in the queueing system GI/M/1; a correction. Biometrika 48, 472–473 (1961).Google Scholar
[5]Lindley, D. V., The theory of queues with a single server. Proc. Camb. Phil. Soc. 48, 277–89 (1952).Google Scholar
[6]Moran, P. A. P.A probability theory of dams and storage systems. Aust. J. Appl. Sci. 5, 116–124 (1954).Google Scholar
[7]Moran, P. A. P., A probability theory of dams and storage systems – modification of the release rule. Aust. J. Appl. Sci. 6, 117–130 (1955).Google Scholar