Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
Glukhov, M. M.
Stelletskii, I. V.
and
Fofanova, T. S.
1972.
Algebra and Geometry.
p.
111.
Yagzhev, A. V.
1974.
Lattice definability of certain matrix algebras.
Algebra and Logic,
Vol. 13,
Issue. 1,
p.
57.
Chupina, E. I.
1988.
Lattice-definability of semisimple finite-dimensional alternative algebras.
Siberian Mathematical Journal,
Vol. 28,
Issue. 5,
p.
849.
Laliena, Jesús
1990.
Lattice isomorphisms of alternative algebras.
Journal of Algebra,
Vol. 128,
Issue. 2,
p.
335.
José Angel, Anquela
1991.
Lattice definability of semisimple jordan algebras.
Communications in Algebra,
Vol. 19,
Issue. 5,
p.
1409.
Cortés, Teresa
1993.
A note on the lattice definability of bernstein algebras.
Linear Algebra and its Applications,
Vol. 179,
Issue. ,
p.
203.
Korobkov, S. S.
2013.
Projections of Monogenic Algebras.
Algebra and Logic,
Vol. 52,
Issue. 5,
p.
392.
Korobkov, S. S.
2015.
Projections of Galois Rings.
Algebra and Logic,
Vol. 54,
Issue. 1,
p.
10.
Korobkov, Sergei Samsonovich
2017.
Решеточная определяемость некоторых матричных колец.
Математический сборник,
Vol. 208,
Issue. 1,
p.
97.
Korobkov, S S
2017.
Lattice definability of certain matrix rings.
Sbornik: Mathematics,
Vol. 208,
Issue. 1,
p.
90.
Korobkov, S. S.
2019.
Projections of Finite Nonnilpotent Rings.
Algebra and Logic,
Vol. 58,
Issue. 1,
p.
48.
Gein, A. G.
2020.
Associative Algebras with a Distributive Lattice of Subalgebras.
Algebra and Logic,
Vol. 59,
Issue. 5,
p.
349.
Korobkov, S. S.
2022.
Projections of Semilocal Rings.
Algebra and Logic,
Vol. 61,
Issue. 2,
p.
125.
Korobkov, S. S.
2023.
Projections of Finite Rings.
Algebra and Logic,
Vol. 62,
Issue. 4,
p.
353.
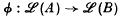 of ℒ(A) onto ℒ(B). We investigate the extent to which the algebra B is determined by the assumption that it is ℒ-isomorphic to a given algebra A. In this paper, we are mainly concerned with the case in which A is a finite- dimensional semi-simple algebra.
of ℒ(A) onto ℒ(B). We investigate the extent to which the algebra B is determined by the assumption that it is ℒ-isomorphic to a given algebra A. In this paper, we are mainly concerned with the case in which A is a finite- dimensional semi-simple algebra.

