Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-03T00:15:02.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite product expansions for matrix n-th roots

Published online by Cambridge University Press:  09 April 2009

R. A. Smith
R. A. Smith
Affiliation:
Department of MathematicsUniversity of Durham, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper a denotes a square matrix with real or complex elements (though the theorems and their proofs are valid in any Banach algebra). Its spectral radius p(a) is given by 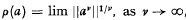with any matrix norm (see [4], p. 183). If p(a) < 1 and n is a positive integer then the binomial series 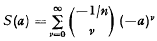converges and its sum satisfies S(a)n = (1−a)−1. Let 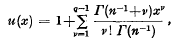where q is any integer exceeding 1. Then u(a) is the sum of the first q terms of the series (2). Write 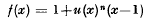and let a0, a1, a2,…be the sequence of matrices obtained by the iterative procedure 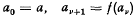Defining polynomials φ0(x), φ1(x), φ2(x),…inductively by 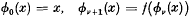we have aν = φν (a) and therefore aμaν = aνaμ for all 4 μ, ν. The following is proved in section 2: Theorem 1. If ρ(a) < 1 then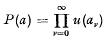converges and P(a) = S(a). Furthermore, if p(a) < r < 1, then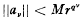for all ν, where M depends on r and a but is independent of ν and q.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 2 , May 1968 , pp. 242 - 249
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Altman, M., ‘An optimum cubically convergent iterative method for inverting a linear bounded operator in Hilbert space’, Pacific J. Math. 10 (1960), 1107–1113.CrossRefGoogle Scholar
[2]Hardy, G. H., Littlewood, J. E. and Polya, G., Inequalities (C.U.P., 2nd ed. 1952).Google Scholar
[3]Hotelling, H., ‘Some new methods in matrix calculation’, Ann. Math. Statist. 14 (1943), 1–34.CrossRefGoogle Scholar
[4]Householder, A. S., The theory of matrices in numerical analysis (Blaisdell, New York, 1964).Google Scholar
[5]Laasonen, P., ‘On the iterative solution of the matrix equation AX 2−I = O’, Math. Tables Aids Comput. 12 (1958), 109–116.CrossRefGoogle Scholar
[6]Ostrowski, A., ‘Sur quelques transformations de la série de Liouville-Neumann’, C.R. Acad. Sci. Paris 206 (1938), 1345–1347.Google Scholar
[7]Petryshyn, W. V., ‘On the inversion of matrices and linear operators’, Proc. A mer. Math. Soc. 16 (1965), 893–901.CrossRefGoogle Scholar
‘8’Traub, J. F., ‘Comparison of iterative methods for the calculation of n-th roots’, Comm. ACM 4 (1961), 143–145.CrossRefGoogle Scholar