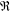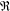Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Yuping
2021.
Nonlinear Jordan derivations of incidence algebras.
Communications in Algebra,
Vol. 49,
Issue. 8,
p.
3200.
Bhushan, Bharat
Sandhu, Gurninder S.
and
Kumar, Deepak
2023.
Centrally-extended generalized Jordan derivations in rings.
Annales Universitatis Paedagogicae Cracoviensis. Studia Mathematica,
Vol. 22,
Issue. 1,
p.
33.