Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tang, Dazhao
2019.
Vanishing coefficients in some q-series expansions.
International Journal of Number Theory,
Vol. 15,
Issue. 04,
p.
763.
TANG, DAZHAO
2019.
VANISHING COEFFICIENTS IN FOUR QUOTIENTS OF INFINITE PRODUCT EXPANSIONS.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 2,
p.
216.
CHERN, SHANE
and
TANG, DAZHAO
2020.
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE.
Bulletin of the Australian Mathematical Society,
Vol. 102,
Issue. 3,
p.
387.
Baruah, Nayandeep Deka
and
Kaur, Mandeep
2020.
Some results on vanishing coefficients in infinite product expansions.
The Ramanujan Journal,
Vol. 53,
Issue. 3,
p.
551.
Dou, Donna Q. J.
and
Xiao, Jiejuan
2021.
The 5-dissections of two infinite product expansions.
The Ramanujan Journal,
Vol. 54,
Issue. 3,
p.
475.
Chern, Shane
2021.
Asymptotics for the Taylor coefficients of certain infinite products.
The Ramanujan Journal,
Vol. 55,
Issue. 3,
p.
987.
Tang, Dazhao
2021.
On 5- and 10-dissections for some infinite products.
The Ramanujan Journal,
Vol. 56,
Issue. 2,
p.
425.
Laughlin, James Mc
and
Zimmer, Peter
2022.
Further results on Vanishing Coefficients in infinite products of the form (qb,qp−b;qp)∞3(qjb,q2p−jb;q2p)∞.
International Journal of Number Theory,
Vol. 18,
Issue. 08,
p.
1863.
Chern, Shane
and
Tang, Dazhao
2022.
Vanishing coefficients and identities concerning Ramanujan’s parameters.
The Ramanujan Journal,
Vol. 57,
Issue. 4,
p.
1367.
Tang, Dazhao
2023.
Vanishing Coefficients in Three Families of Products of Theta Functions. II..
Results in Mathematics,
Vol. 78,
Issue. 4,
Tang, Dazhao
2023.
Vanishing coefficients in three families of products of theta functions.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 1,
Du, Julia Q. D.
and
Tang, Dazhao
2023.
Vanishing coefficients in quotients of theta functions with odd moduli.
International Journal of Number Theory,
Vol. 19,
Issue. 10,
p.
2451.
Tang, Dazhao
2023.
Vanishing Coefficients in Two Families of Quotients of Theta Functions.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 1,
Chern, Shane
and
Tang, Dazhao
2024.
General coefficient-vanishing results associated with theta series.
Advances in Applied Mathematics,
Vol. 159,
Issue. ,
p.
102742.
Channabasavayya
Keerthana, Gedela Kavya
and
Dasappa, Ranganatha
2024.
On a generalization of 5-dissections of some infinite q-products.
The Ramanujan Journal,
Vol. 64,
Issue. 4,
p.
1335.
Tang, Dazhao
2024.
VANISHING COEFFICIENTS IN POWERS OF THETA FUNCTIONS WITH ODD MODULI.
Rocky Mountain Journal of Mathematics,
Vol. 54,
Issue. 1,
Channabasavayya
and
Dasappa, Ranganatha
2024.
Vanishing coefficients in arithmetic progressions of some infinite products with modulo 13, 17, 19 and 29.
The Journal of Analysis,
Vol. 32,
Issue. 5,
p.
3101.
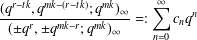 $$\begin{eqnarray}\frac{(q^{r-tk},q^{mk-(r-tk)};q^{mk})_{\infty }}{(\pm q^{r},\pm q^{mk-r};q^{mk})_{\infty }}=:\mathop{\sum }_{n=0}^{\infty }c_{n}q^{n}\end{eqnarray}$$
$$\begin{eqnarray}\frac{(q^{r-tk},q^{mk-(r-tk)};q^{mk})_{\infty }}{(\pm q^{r},\pm q^{mk-r};q^{mk})_{\infty }}=:\mathop{\sum }_{n=0}^{\infty }c_{n}q^{n}\end{eqnarray}$$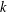 $k$,
$k$, 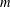 $m$,
$m$,  $s$ and
$s$ and  $t$, where
$t$, where 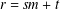 $r=sm+t$, then
$r=sm+t$, then 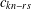 $c_{kn-rs}$ is always zero. Our theorems also partly give a simpler reformulation of results of Alladi and Gordon [‘Vanishing coefficients in the expansion of products of Rogers–Ramanujan type’, in: The Rademacher Legacy to Mathematics (University Park, PA, 1992), Contemporary Mathematics, 166 (American Mathematical Society, Providence, RI, 1994), 129–139], but also give results for cases not covered by the theorems of Alladi and Gordon. We also give some interpretations of the analytic results in terms of integer partitions.
$c_{kn-rs}$ is always zero. Our theorems also partly give a simpler reformulation of results of Alladi and Gordon [‘Vanishing coefficients in the expansion of products of Rogers–Ramanujan type’, in: The Rademacher Legacy to Mathematics (University Park, PA, 1992), Contemporary Mathematics, 166 (American Mathematical Society, Providence, RI, 1994), 129–139], but also give results for cases not covered by the theorems of Alladi and Gordon. We also give some interpretations of the analytic results in terms of integer partitions.