Published online by Cambridge University Press: 26 January 2022
A noncomplete graph is 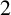 $2$
-distance-transitive if, for
$2$
-distance-transitive if, for 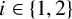 $i \in \{1,2\}$
and for any two vertex pairs
$i \in \{1,2\}$
and for any two vertex pairs 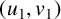 $(u_1,v_1)$
and
$(u_1,v_1)$
and 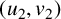 $(u_2,v_2)$
with the same distance i in the graph, there exists an element of the graph automorphism group that maps
$(u_2,v_2)$
with the same distance i in the graph, there exists an element of the graph automorphism group that maps 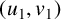 $(u_1,v_1)$
to
$(u_1,v_1)$
to 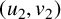 $(u_2,v_2)$
. This paper determines the family of
$(u_2,v_2)$
. This paper determines the family of 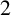 $2$
-distance-transitive Cayley graphs over dihedral groups, and it is shown that if the girth of such a graph is not
$2$
-distance-transitive Cayley graphs over dihedral groups, and it is shown that if the girth of such a graph is not 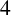 $4$
, then either it is a known
$4$
, then either it is a known 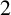 $2$
-arc-transitive graph or it is isomorphic to one of the following two graphs:
$2$
-arc-transitive graph or it is isomorphic to one of the following two graphs: 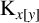 $ {\mathrm {K}}_{x[y]}$
, where
$ {\mathrm {K}}_{x[y]}$
, where 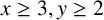 $x\geq 3,y\geq 2$
, and
$x\geq 3,y\geq 2$
, and 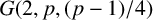 $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and 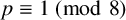 $p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, as an application of the above result, a complete classification is achieved of the family of
$p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, as an application of the above result, a complete classification is achieved of the family of 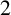 $2$
-geodesic-transitive Cayley graphs for dihedral groups.
$2$
-geodesic-transitive Cayley graphs for dihedral groups.
Communicated by Brian Alspach
Supported by the NNSF of China (12061034,12071484) and NSF of Jiangxi (20212BAB201010,20192ACBL21007,GJJ190273)