Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T20:28:55.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Error analysis of an algorithm for summing certain finite series

Published online by Cambridge University Press:  09 April 2009

David Elliott
David Elliott
Affiliation:
Mathematics DepartmentUniversity of TasmaniaHobart, Tasmania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

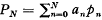An algorithm for summing the series , where the coefficients an are assumed known, and the quantities pn, satisfy a linear three term recurrence relation, has been given by Clenshaw [1]. If we suppose that the pn satisfy the recurrence relation 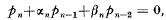where αn and βn are, in general, functions of n, then PN may be found by constructing a sequence {bn} for n = N(−1)0, where the b satisfy the inhomogeneous recurrence relation 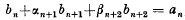with the conditions, 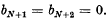The sum PN is then given by 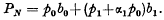This result can be readily verified by multiplying each side of equation (1.2) by pn, summing from n = 0 to N, and making use of equations (1.1) and (1.3).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 2 , May 1968 , pp. 213 - 221
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Clenshaw, C. W., ‘A note on the summation of Chebyshev series’, M.T.A.C. 9 (1955), 118–120.Google Scholar
[2]Elliott, D., ‘On the expansion of functions in ultraspherical polynomials’, Journ. Aust. Math. Soc. 1 (1960), 428–438.Google Scholar
[3]Smith, F. J., ‘An algorithm for summing orthogonal polynomial series and their derivatives with applications to curve-fitting and interpolation’, Math. Comp. 19 (1965), 33–36.Google Scholar
[4]Milne-Thomson, L. M., The calculus of finite differences, (Macmillan, London, 1933).Google Scholar
[5]Olver, F. W. J., ‘Error analysis of Miller's recurrence algorithm’, Math. Comp. 18 (1964), 65–74.Google Scholar