No CrossRef data available.
Published online by Cambridge University Press: 21 November 2019
The Chebyshev conjecture posits that Chebyshev subsets of a real Hilbert space 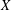 $X$ are convex. Works by Asplund, Ficken and Klee have uncovered an equivalent formulation of the Chebyshev conjecture in terms of uniquely remotal subsets of
$X$ are convex. Works by Asplund, Ficken and Klee have uncovered an equivalent formulation of the Chebyshev conjecture in terms of uniquely remotal subsets of 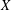 $X$. In this tradition, we develop another equivalent formulation in terms of Chebyshev subsets of the unit sphere of
$X$. In this tradition, we develop another equivalent formulation in terms of Chebyshev subsets of the unit sphere of  $X\times \mathbb{R}$. We characterise such sets in terms of the image under stereographic projection. Such sets have superior structure to Chebyshev sets and uniquely remotal sets.
$X\times \mathbb{R}$. We characterise such sets in terms of the image under stereographic projection. Such sets have superior structure to Chebyshev sets and uniquely remotal sets.