Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T09:09:19.008Z Has data issue: false hasContentIssue false
  • English
  • Français

BOUNDED TOEPLITZ AND HANKEL PRODUCTS ON THE WEIGHTED BERGMAN SPACES OF THE UNIT BALL

Part of: Holomorphic functions of several complex variables Special classes of linear operators

Published online by Cambridge University Press:  05 June 2015

MAŁGORZATA MICHALSKA  and
PAWEŁ SOBOLEWSKI
MAŁGORZATA MICHALSKA
Affiliation:
Instytut Matematyki UMCS, pl. Marii Curie-Skłodowskiej 1, 20-031 Lublin, Poland email [email protected]
PAWEŁ SOBOLEWSKI*
Affiliation:
Instytut Matematyki UMCS, pl. Marii Curie-Skłodowskiej 1, 20-031 Lublin, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 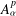$A_{{\it\alpha}}^{p}$ be the weighted Bergman space of the unit ball in 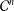${\mathcal{C}}^{n}$, 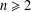$n\geq 2$. Recently, Miao studied products of two Toeplitz operators defined on 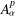$A_{{\it\alpha}}^{p}$. He proved a necessary condition and a sufficient condition for boundedness of such products in terms of the Berezin transform. We modify the Berezin transform and improve his sufficient condition for products of Toeplitz operators. We also investigate products of two Hankel operators defined on 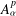$A_{{\it\alpha}}^{p}$, and products of the Hankel operator and the Toeplitz operator. In particular, in both cases, we prove sufficient conditions for boundedness of the products.

Keywords

Toeplitz operatorsHankel operatorsweighted Bergman spaces

MSC classification

Primary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Secondary: 32A36: Bergman spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 2 , October 2015 , pp. 237 - 249
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Conway, J. B., Functions of One Complex Variable, 2nd edn, Graduate Texts in Mathematics, 11 (Springer, New York, Berlin, 1978).CrossRefGoogle Scholar
Cruz-Uribe, D., ‘The invertibility of the product of unbounded Toeplitz operators’, Integral Equations Operator Theory 20(2) (1994), 231–237.CrossRefGoogle Scholar
Lu, Y. and Liu, Ch., ‘Toeplitz and Hankel products on Bergman spaces of the unit ball’, Chin. Ann. Math. B 30(3) (2009), 293–310.CrossRefGoogle Scholar
Miao, J., ‘Bounded Toeplitz products on the weighted Bergman spaces of the unit ball’, J. Math. Anal. Appl. 346 (2008), 305–313.CrossRefGoogle Scholar
Michalska, M., Nowak, M. and Sobolewski, P., ‘Bounded Toeplitz and Hankel products on weighted Bergman spaces of the unit ball’, Ann. Polon. Math. 99(1) (2010), 45–53.CrossRefGoogle Scholar
Nazarov, F., ‘A counterexample to Sarason’s conjecture’, Preprint available online atwww.math.msu.edu/∼fedja/prepr.html.Google Scholar
Park, J. D., ‘Bounded Toeplitz products on the Bergman space of the unit ball in Cn’, Integral Equations Operator Theory 54(4) (2006), 571–584.CrossRefGoogle Scholar
Pott, S. and Strouse, E., ‘Products of Toeplitz operators on the Bergman spaces A 𝛼2’, St. Petersburg Math. J. 18(1) (2007), 105–118.CrossRefGoogle Scholar
Rudin, W., Functional Analysis, McGraw-Hill Series in Higher Mathematics, 397 (McGraw-Hill, New York, Düsseldorf, Johannesburg, 1973).Google Scholar
Rudin, W., Function Theory in the Unit Ball of C n, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science], 241 (Springer, New York, Berlin, 1980).CrossRefGoogle Scholar
Sarason, D., ‘Products of Toeplitz operators’, in: Linear and Complex Analysis Problem Book 3, Lecture Notes in Mathematics, 1573 (Springer, Berlin, New York, 1994), 318–319.Google Scholar
Stroethoff, K. and Zheng, D., ‘Products of Hankel and Toeplitz operators on the Bergman space’, J. Funct. Anal. 169 (1999), 289–313.CrossRefGoogle Scholar
Stroethoff, K. and Zheng, D., ‘Bounded Toeplitz products on the Bergman space of the polydisk’, J. Math. Anal. Appl. 278(1) (2003), 125–135.CrossRefGoogle Scholar
Stroethoff, K. and Zheng, D., ‘Bounded Toeplitz products on Bergman spaces of the unit ball’, J. Math. Anal. Appl. 325 (2007), 114–129.CrossRefGoogle Scholar
Stroethoff, K. and Zheng, D., ‘Bounded Toeplitz products on weighted Bergman spaces’, J. Operator Theory 59(2) (2008), 277–308.Google Scholar
Zheng, D., ‘The distribution function inequality and products of Toeplitz and Hankel operators’, J. Funct. Anal. 138 (1996), 477–501.CrossRefGoogle Scholar
Zhu, K., Spaces of Holomorphic Functions in the Unit Ball, Graduate Texts in Mathematics, 226 (Springer, New York, 2005).Google Scholar