Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T07:57:56.667Z Has data issue: false hasContentIssue false
  • English
  • Français

Application of the Ritz method to non-standard eigenvalue problems

Published online by Cambridge University Press:  09 April 2009

A. L. Andrew
A. L. Andrew
Affiliation:
La trobe University Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There is an extensive literature on application of the Ritz method to eigenvalue problems of the type 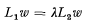where L1, L2 are positive definite linear operators in a Hilbert space (see for example [1]). The classical theory concerns the case in which there exists a minimum (or maximum) eigenvalue, and subsequent eigenvalues can be located by a well-known mini-max principle [2; p. 405]. This paper considers the possibility of application of the Ritz method to eigenvalue problems of the type (1) where the linear operators L1L2 are not necessarily positive definite and a minimum (or maximum) eigenvalue may not exist. The special cases considered may be written with the eigenvalue occurring in a non-linear manner.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 3-4 , November 1969 , pp. 367 - 384
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Mikhlin, S. G., Variational methods in mathematical physics (Pergamon, 1964).Google Scholar
[2]Courant, R. and Hilbert, D., Methods of mathematical physics. Vol. 1 (Interscience, 1953).Google Scholar
[3]Andrew, A. L., ‘Higher modes of non-radial oscillations of stars by variational methods’, Aust. J. Phys. 20 (1967), 363–368.CrossRefGoogle Scholar
[4]Chandrasekhar, S., ‘A general variational principle governing the radial and the non-radial oscillations of gaseous masses’, Astrophys. J. 139 (1964), 664–674.CrossRefGoogle Scholar
[5]Ledoux, P. and Walraven, Th., ‘Variable stars’, in Flügge, S., Handbuch der Physik, Vol. 51, (Springer, Berlin, 1958), 353–604.Google Scholar
[6]Lebovitz, N. R., ‘On Schwarzschild's criterion for the stability of gaseous masses’, Astrophys. J. 142 (1965), 229–242.Google Scholar
[7]Cowling, T. G., ‘The non-radial oscillations of polytropic stars’, Monthly Notices Roy. Astronom. Soc. 101 (1941) 367–375.Google Scholar
[8]Ledoux, P. and Smeyers, P., ‘Sur le spectre des oscillations non radiales d'un modèle stellaire’ C. R. Acad. Sci. Paris. Sér. B 262 (1966), 841–844.Google Scholar
[9]Owen, J. W., ‘The non-radial oscillations of centrally condensed stars’, Monthly Notices Roy. Astronom. Soc. 117 (1957), 384–392.CrossRefGoogle Scholar
[10]Van der Borght, R., ‘The evolution of massive stars initially composed of pure hydrogen’, Aust. J. Phys. 17 (1964), 165–174.CrossRefGoogle Scholar
[11]Wan, Fook Sun and Van der Borght, R., ‘Note on Cowling's method in the theory of non-radial oscillations of massive stars’, Aust. J. Phys. 19 (1966), 467–470.Google Scholar
[12]Andrew, A. L., ‘A note on the Ritz method with an application to overtone stellar pulsation theory’, J. Aust. Math. Soc. 8 (1968), 275–286.CrossRefGoogle Scholar
[13]Chandrasekhar, S. and Lebovitz, N. R., ‘Non-radial oscillations of gaseous masses’, Astrophys. J. 140 (1964), 1517–1528.CrossRefGoogle Scholar
[14]Robe, H. and Brandt, L., ‘Sur les oscillations non radiales des polytropes’, Ann. Astrophys. 29 (1966), 517–524.Google Scholar
[15]Tassoul, J. L., ‘Sur l'instabilité convective d'une masse gazeuse inhomogàne’, Ann. Astrophys. 30 (1967), 363–370.Google Scholar
[16]Robe, H., ‘Sur les oscillations non radiales d'une sphère’, Acad. Roy. Belg. Bull. Cl. Sci. 51 (1965), 598–603.Google Scholar
[17]Marcus, M., ‘Basic theorems in matrix theory’, Nat. Bur. Standards Appl. Math. Ser. 57 (1960).Google Scholar
[18]Mihlin, S. G. (Mikhlin), ‘The stability of the Ritz method’, Soviet Math. Dokl. 1 (1960), 1230–1233.Google Scholar
[19]Lebovitz, N. R., ‘On the onset of convective instability’, Astrophys. J. 142 (1965), 1257–1260.CrossRefGoogle Scholar
[20]Andrew, A. L., ‘Non-radial oscillations of massive stars by variational methods’, Acad. Roy. Belg. Bull. Cl. Sci. 54 (1968), (1046–1055).Google Scholar