Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T09:46:17.054Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXPLICIT DESCRIPTION OF THE SIMPLICIAL GROUP $K(A, n)$

Part of: Homological algebra Connections with homological algebra and category theory

Published online by Cambridge University Press:  07 June 2013

MIHAI D. STAIC
MIHAI D. STAIC*
Affiliation:
Department of Mathematics and Statistics, Bowling Green State University, Bowling Green, OH 43403, USA Institute of Mathematics of the Romanian Academy, PO. BOX 1-764, RO-70700, Bucharest, Romania
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give an explicit construction for a 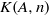$K(A, n)$ simplicial group and explain its topological interpretation.

Keywords

simplicial groupsgroup cohomologyHopf algebras

MSC classification

Secondary: 18G30: Simplicial sets, simplicial objects (in a category) 20J06: Cohomology of groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 1 , August 2013 , pp. 133 - 144
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Connes, A. and Moscovici, H., ‘Cyclic cohomology and Hopf algebras’, Lett. Math. Phys. 48 (1) (1999), 97–108.CrossRefGoogle Scholar
Crainic, M., ‘Cyclic cohomology of Hopf algebras’, J. Pure Appl. Algebra 166 (1) (2002), 29–66.CrossRefGoogle Scholar
Eilenberg, S. and MacLane, S., ‘Determination of the second homology and cohomology groups of a space by means of homotopy invariants’, Proc. Nat. Acad. Sci. USA 32 (1946), 277–280.CrossRefGoogle ScholarPubMed
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics, 174 (Birkhäuser, Basel, 1999).CrossRefGoogle Scholar
Khalkhali, M. and Rangipour, B., ‘A new cyclic module for Hopf algebras’, K-Theory 27 (2002), 111–131.CrossRefGoogle Scholar
Loday, J. L., Cyclic Homology, Grundlehren der Mathematischen Wissenschaften, 301 (Springer, Berlin, 1992).CrossRefGoogle Scholar
May, J. P., Simplicial Objects in Algebraic Topology, Chicago Lectures in Mathematics (1967).Google Scholar
Staic, M. D., ‘Secondary cohomology and k-invariants’, Bull. Belg. Math. Soc. 19 (3) (2012), 561–572.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics (1995).Google Scholar