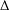 $\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN
$\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN 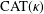 $\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
$\text{CAT}(\unicode[STIX]{x1D705})$ SPACESPublished online by Cambridge University Press: 14 May 2020
We first introduce the weighted averaged projection sequence in 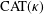 $\text{CAT}(\unicode[STIX]{x1D705})$ spaces and then we establish some inequalities for the weighted averaged projection sequence. Using the inequalities, we prove the asymptotic regularity and the
$\text{CAT}(\unicode[STIX]{x1D705})$ spaces and then we establish some inequalities for the weighted averaged projection sequence. Using the inequalities, we prove the asymptotic regularity and the 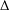 $\unicode[STIX]{x1D6E5}$-convergence of the weighted averaged projection sequence. Furthermore, we prove the strong convergence of the sequence under certain regularity or compactness conditions on
$\unicode[STIX]{x1D6E5}$-convergence of the weighted averaged projection sequence. Furthermore, we prove the strong convergence of the sequence under certain regularity or compactness conditions on 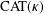 $\text{CAT}(\unicode[STIX]{x1D705})$ spaces.
$\text{CAT}(\unicode[STIX]{x1D705})$ spaces.
Communicated by G. Wilkin
The author was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2017R1C1B1005334) and the 2020 scientific promotion program funded by Jeju National University.