Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T09:14:30.889Z Has data issue: false hasContentIssue false
  • English
  • Français

A RESULT OF PALEY AND WIENER ON DAMEK–RICCI SPACES

Part of: Lie groups Abstract harmonic analysis

Published online by Cambridge University Press:  03 May 2019

MITHUN BHOWMIK
MITHUN BHOWMIK*
Affiliation:
Stat-Math Unit, Indian Statistical Institute, 203 B. T. Road, Kolkata-700108, India
Get access Rights & Permissions [Opens in a new window]

Abstract

A classical result due to Paley and Wiener characterizes the existence of a nonzero function in 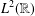$L^{2}(\mathbb{R})$, supported on a half-line, in terms of the decay of its Fourier transform. In this paper, we prove an analogue of this result for Damek–Ricci spaces.

Keywords

Damek–Ricci spaceFourier transformPaley–Wiener theorem

MSC classification

Primary: 22E30: Analysis on real and complex Lie groups
Secondary: 43A85: Analysis on homogeneous spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 1 , August 2020 , pp. 1 - 16
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by Research Fellowship from Indian Statistical Institute, India.

†

Current address: Department of Mathematics, Indian Institute of Technology, Bombay, Powai, Mumbai-400076, India email [email protected], [email protected]

References

Anker, J., Damek, E. and Yacoub, C., ‘Spherical analysis on harmonic AN groups’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 23(4) (1996), 643–679.Google Scholar
Astengo, F., Camporesi, R. and Di Blasio, B., ‘The Helgason Fourier transform on a class of nonsymmetric harmonic spaces’, Bull. Aust. Math. Soc. 55(3) (1997), 405–424.Google Scholar
Astengo, F. and Di Blasio, B., ‘A Paley–Wiener theorem on NA harmonic spaces’, Colloq. Math. 80(2) (1999), 211–233.Google Scholar
Bhowmik, M. and Sen, S., ‘An uncertainty principle of Paley and Wiener on Euclidean Motion Group’, J. Fourier Anal. Appl. 23(6) (2017), 1445–1464.Google Scholar
Bhowmik, M. and Sen, S., ‘Uncertainty Principles of Ingham and Paley–Wiener on Semisimple Lie groups’, Israel J. Math. 225(1) (2018), 193–221.Google Scholar
Cowling, M., Dooley, A., Korányi, A. and Ricci, F., ‘An approach to symmetric spaces of rank one via groups of Heisenberg type’, J. Geom. Anal. 8(2) (1998), 199–237.Google Scholar
Damek, E., ‘Curvature of a semidirect extension of a Heisenberg type nilpotent group’, Colloq. Math. 53(2) (1987), 249–253.Google Scholar
Damek, E. and Ricci, F., ‘A class of nonsymmetric harmonic Riemannian spaces’, Bull. Amer. Math. Soc. (N.S.) 27(1) (1992), 139–142.Google Scholar
Faraut, J., ‘Un thorme de Paley–Wiener pour la transformation de Fourier sur un espace Riemannien symtrique de rang un’, J. Funct. Anal. 49(2) (1982), 230–268.Google Scholar
Helgason, S., Geometric Analysis on Symmetric Spaces, Mathematical Surveys and Monographs, 39 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Helgason, S., The Radon Transform, 2nd edn, Progress in Mathematics, 5 (Birkhäuser, Boston, MA, 1999).Google Scholar
Ingham, A. E., ‘A Note on Fourier Transforms’, J. Lond. Math. Soc. S1‐9(1) (1934), 29–32.Google Scholar
Koosis, P., The logarithmic integral I, Cambridge Studies in Advanced Mathematics, 12 (Cambridge University Press, Cambridge, 1998).Google Scholar
Levinson, N., Gap and Density Theorems, American Mathematical Society Colloquium Publications, 26 (American Mathematical Society, New York, 1940).Google Scholar
Levinson, N., ‘On a class of nonvanishing functions’, Proc. Lond. Math. Soc. (2) 41(5) (1936), 393–407.Google Scholar
Paley, R. E. A. C. and Wiener, N., Fourier Transforms in the Complex Domain (Reprint of the 1934 original), American Mathematical Society Colloquium Publications, 19 (American Mathematical Society, Providence, RI, 1987).Google Scholar
Paley, R. E. A. C. and Wiener, N., ‘Notes on the theory and application of Fourier transforms. I, II’, Trans. Amer. Math. Soc. 35(2) (1933), 348–355.Google Scholar
Ray, S. K. and Sarkar, R. P., ‘Fourier and Radon transform on harmonic NA groups’, Trans. Amer. Math. Soc. 361(8) (2009), 4269–4297.Google Scholar
Stein, E. M. and Shakarchi, R., Complex Analysis, Princeton Lectures in Analysis, II (Princeton University Press, Princeton, NJ, 2003).Google Scholar