Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T09:39:22.508Z Has data issue: false hasContentIssue false
  • English
  • Français

ON EDGE-PRIMITIVE GRAPHS WITH SOLUBLE EDGE-STABILIZERS

Part of: Permutation groups Graph theory

Published online by Cambridge University Press:  06 August 2021

HUA HAN Open the ORCID record for HUA HAN [Opens in a new window] ,
HONG CI LIAO  and
ZAI PING LU Open the ORCID record for ZAI PING LU [Opens in a new window]
HUA HAN
Affiliation:
School of Science, Tianjin University of Technology, Tianjin300384, PR China e-mail: [email protected]
HONG CI LIAO
Affiliation:
Center for Combinatorics, LPMC, Nankai University, Tianjin300071, PR China e-mail: [email protected]
ZAI PING LU*
Affiliation:
Center for Combinatorics, LPMC, Nankai University, Tianjin300071, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph is edge-primitive if its automorphism group acts primitively on the edge set, and 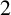$2$ -arc-transitive if its automorphism group acts transitively on the set of 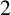$2$ -arcs. In this paper, we present a classification for those edge-primitive graphs that are 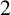$2$ -arc-transitive and have soluble edge-stabilizers.

Keywords

edge-primitive graph2-arc-transitive graphalmost simple group2-transitive groupsoluble group

MSC classification

Primary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 2 , October 2022 , pp. 160 - 187
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Michael Giudici

The third author was supported by the National Natural Science Foundation of China (11971248 and 11731002) and the Fundamental Research Funds for the Central Universities.Michael Giudici

References

Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups (Cambridge University Press, New York, 2013).CrossRefGoogle Scholar
Cameron, P. J., Permutation Groups (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Conway, J. H., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups (Clarendon Press, Oxford, 1985).Google Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, New York, 1996).CrossRefGoogle Scholar
Fang, X. G. and Praeger, C. E., ‘Finite two-arc transitive graphs admitting a Suzuki simple group’, Comm. Algebra 27 (1999), 3727–3754.CrossRefGoogle Scholar
Foulser, D. A., ‘The flag-transitive collineation groups of the Desarguesian affine planes’, Canad. J. Math. 16 (1964), 443–472.CrossRefGoogle Scholar
Gardiner, A., ‘Arc transitivity in graphs’, Q. J. Math. 24 (1973), 399–407.CrossRefGoogle Scholar
Giudici, M. and King, C. S. H., ‘On edge-primitive $3$ -arc-transitive graphs’, J. Combin. Theory Ser. B 151 (2021), 282–306.CrossRefGoogle Scholar
Giudici, M. and Li, C. H., ‘On finite edge-primitive and edge-quasiprimitive graphs’, Q. J. Math. 100 (2010), 275–298.Google Scholar
Guo, S. T., Feng, Y. Q. and Li, C. H., ‘The finite edge-primitive pentavalent graphs’, J. Algebraic Combin. 38 (2013), 491–497.CrossRefGoogle Scholar
Guo, S. T., Feng, Y. Q. and Li, C. H., ‘Edge-primitive tetravalent graphs’, J. Combin. Theory Ser. B 112 (2015), 124–137.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin and New York, 1967).CrossRefGoogle Scholar
Kleidman, P. B., ‘The maximal subgroups of the finite $8$ -dimensional orthogonal group ${\mathrm{P}\Omega}_8^{+}(q)$ and of their automorphism groups’, J. Algebra 110 (1987), 173–242.CrossRefGoogle Scholar
Kleidman, P. B., ‘The maximal subgroups of the Steinberg triality groups 3D4(q) and of their automorphism groups’, J. Algebra 115 (1988), 182–199.CrossRefGoogle Scholar
Kleidman, P. B., ‘The maximal subgroups of the Chevalley groups ${G}_2(q)$ and with $q$ odd, the Ree group 2G2(q), and their automorphism groups’, J. Algebra 117 (1988), 30–71.CrossRefGoogle Scholar
Li, C. H., Seress, Á. and Song, S. J., ‘ s-arc-transitive graphs and normal subgroups’, J. Algebra 421 (2015), 331–348.CrossRefGoogle Scholar
Li, C. H. and Zhang, H., ‘The finite primitive groups with soluble stabilizers, and the edge-primitive $s$ -arc transitive graphs’, Proc. Lond. Math. Soc. 103 (2011), 441–472.CrossRefGoogle Scholar
Liebeck, M. W., Praeger, C. E. and Saxl, J., ‘A classification of the maximal subgroups of the finite alternating and symmetric groups’, J. Algebra 111 (1987), 365–383.CrossRefGoogle Scholar
Liebeck, M. W., Saxl, J. and Seitz, G. M., ‘Subgroups of maximal rank in finite exceptional groups of Lie type’, Proc. Lond. Math. Soc. 65 (1992), 297–325.CrossRefGoogle Scholar
Liebeck, M. W. and Seitz, G. M., ‘A survey of maximal subgroups of exceptional groups of Lie type’, in: Groups, Combinatorics $\&$ Geometry, Durham, 2001 (eds. Ivanov, A. A., Liebeck, M. W. and Saxl, J.) (World Scientific, River Edge, NJ, 2003), 139–146.CrossRefGoogle Scholar
Lu, Z. P., ‘On edge-primitive $2$ -arc-transitive graphs’, J. Combin. Theory Ser. A 171 (2020), 105172.CrossRefGoogle Scholar
Malle, G., ‘The maximal subgroups of 2F4(q 2)’, J. Algebra 139 (1991), 52–69.CrossRefGoogle Scholar
Norton, S. P. and Wilson, R. A, ‘A correction to the $41$ -structure of the Monster, a construction of a new maximal subgroup ${\mathsf{L}}_2(41)$ and a new moonshine phenomenon’, J. Lond. Math. Soc. (2) 87 (2013), 943–962.CrossRefGoogle Scholar
Pan, J. M., Wu, C. X. and Yin, F. G., ‘Finite edge-primitive graphs of prime valency’, European J. Combin. 73 (2018), 61–71.CrossRefGoogle Scholar
Praeger, C. E., ‘An O’Nan–Scott theorem for finite quasiprimitive permutation groups and an application to $2$ -arc transitive graphs’, J. Lond. Math. Soc. (2) 47 (1992), 227–239.Google Scholar
Praeger, C. E., ‘On a reduction theorem for finite, bipartite 2-arc-transitive graphs’, Australas. J. Combin. 7 (1993), 21–36.Google Scholar
Suzuki, M., ‘On a class of doubly transitive groups’, Ann. Math. 75 (1962), 105–145.CrossRefGoogle Scholar
The GAP Group, GAP—Groups, Algorithms, and Programming—A System for Computational Discrete Algebra, Version 4.11.1, 2021. http://www.gap-system.org.Google Scholar
Trofimov, V. I., ‘Vertex stabilizers of locally projective groups of automorphisms of graphs: a summary’, in: Groups, Combinatorics $\&$ Geometry, Durham, 2001 (eds. Ivanov, A. A., Liebeck, M. W. and Saxl, J.) (World Scientific, River Edge, NJ, 2003), 313–326.CrossRefGoogle Scholar
Weiss, R., ‘Symmetric graphs with projective subconstituents’, Proc. Amer. Math. Soc. 72 (1978), 213–217.CrossRefGoogle Scholar
Weiss, R., ‘Groups with a $\left(B,N\right)$ -pair and locally transitive graphs’, Nagoya Math. J. 74 (1979), 1–21.CrossRefGoogle Scholar
Weiss, R., ‘The nonexistence of $8$ -transitive graphs’, Combinatorica 1 (1981), 309–311.CrossRefGoogle Scholar
Weiss, R., ‘ s-transitive graphs’, in: Algebraic Methods in Graph Theory, Colloquia Mathematica Societatis Janos Bolyai, 25 (North-Holland, Amsterdam and New York, 1981), 827–847.Google Scholar
Weiss, R. M., ‘Kantenprimitive Graphen vom Grad drei’, J. Combin. Theory Ser. B 15 (1973), 269–288 (in German).CrossRefGoogle Scholar
Wilson, R. A., ‘The maximal subgroups of the Baby Monster. I’, J. Algebra 211 (1999), 1–14.CrossRefGoogle Scholar
Wilson, R. A., The Finite Simple Groups (Springer, London, 2009).CrossRefGoogle Scholar
Zsigmondy, K., ‘Zur Theorie der Potenzreste’, Monatsch. Math. Phys. 3 (1892), 265–284 (in German).CrossRefGoogle Scholar