Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-10T16:01:43.705Z Has data issue: false hasContentIssue false
  • English
  • Français

HYPERREFLEXIVITY CONSTANTS OF THE BOUNDED 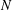$N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS

Part of: Abstract harmonic analysis Selfadjoint operator algebras Special classes of linear operators

Published online by Cambridge University Press:  30 April 2019

EBRAHIM SAMEI  and
JAFAR SOLTANI FARSANI
EBRAHIM SAMEI*
Affiliation:
Department of Mathematics & Statistics, University of Saskatchewan, 106 Wiggins Road, Saskatoon, SK, Canada email [email protected] Institute of Mathematics of the Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland
JAFAR SOLTANI FARSANI
Affiliation:
Department of Mathematics & Statistics, University of Saskatchewan, 106 Wiggins Road, Saskatoon, SK, Canada email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the concept of strong property 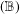$(\mathbb{B})$ with a constant for Banach algebras and, by applying a certain analysis on the Fourier algebra of the unit circle, we show that all C*-algebras and group algebras have the strong property 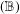$(\mathbb{B})$ with a constant given by $288\unicode[STIX]{x1D70B}(1+\sqrt{2})$. We then use this result to find a concrete upper bound for the hyperreflexivity constant of 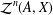${\mathcal{Z}}^{n}(A,X)$, the space of bounded $n$-cocycles from 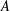$A$ into 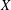$X$, where 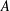$A$ is a C*-algebra or the group algebra of a group with an open subgroup of polynomial growth and $X$ is a Banach $A$-bimodule for which 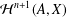${\mathcal{H}}^{n+1}(A,X)$ is a Banach space. As another application, we show that for a locally compact amenable group 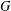$G$ and 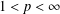$1<p<\infty$, the space 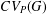$CV_{P}(G)$ of convolution operators on 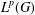$L^{p}(G)$ is hyperreflexive with a constant given by 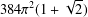$384\unicode[STIX]{x1D70B}^{2}(1+\sqrt{2})$. This is the generalization of a well-known result of Christensen [‘Extensions of derivations. II’, Math. Scand. 50(1) (1982), 111–122] for 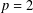$p=2$.

Keywords

reflexivityhyperreflexivityhyperreflexivity constantn-cocyclesC*-algebrasgroup algebrasgroups with polynomial growthamenability

MSC classification

Primary: 47B47: Commutators, derivations, elementary operators, etc.
Secondary: 46L05: General theory of $C^*$-algebras 43A20: $L^1$-algebras on groups, semigroups, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 1 , August 2020 , pp. 112 - 130
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alaminos, J., Extremera, J. and Villena, A. R., ‘Approximately zero product preserving maps’, Israel J. Math. 178 (2010), 1–28.10.1007/s11856-010-0055-4Google Scholar
Alaminos, J., Extremera, J. and Villena, A. R., ‘Hyperreflexivity of the derivation space of some group algebras’, Math. Z. 266 (2010), 571–582.Google Scholar
Alaminos, J., Extremera, J. and Villena, A. R., ‘Hyperreflexivity of the derivation space of some group algebras, II’, Bull. Lond. Math. Soc. 44(2) (2012), 323–335.10.1112/blms/bdr096Google Scholar
Arveson, W. B., ‘Interpolation problems in nest algebras’, J. Funct. Anal. 20(3) (1975), 208–233.Google Scholar
Bresar, M. and Semri, P., ‘Mappings which preserve idempotents, local automorphisms and local derivations’, Canad. J. Math. 45(3) (1975), 483–496.10.4153/CJM-1993-025-4Google Scholar
Christensen, E., ‘Extensions of derivations. II’, Math. Scand. 50(1) (1982), 111–122.Google Scholar
Crist, R. L., ‘Local derivations on operator algebras’, J. Funct. Anal. 135(1) (1996), 76–92.Google Scholar
Dales, H. G., Banach Algebras and Automatic Continuity (Oxford University Press, New York, 2000).Google Scholar
Hadwin, D. and Li, J., ‘Local derivations and local automorphisms’, J. Math. Anal. Appl. 290(2) (2004), 702–714.Google Scholar
Hadwin, D. and Li, J., ‘Local derivations and local automorphisms on some algebras’, J. Operator Theory 60(1) (2008), 29–44.Google Scholar
Jing, W., ‘Local derivations of reflexive algebras’, Proc. Amer. Math. Soc. 125(3) (1997), 869–873.Google Scholar
Jing, W., ‘Local derivations of reflexive algebras II’, Proc. Amer. Math. Soc. 129(6) (2001), 1733–1737.Google Scholar
Jing, W. and Lu, S., ‘Topological reflexivity of the spaces of (𝛼, 𝛽)-derivations on operator algebras’, Studia Math. 156(2) (2003), 121–131.Google Scholar
Johnson, B. E., ‘Local derivations on C*-algebras are derivations’, Trans. Amer. Math. Soc. 353 (2000), 313–325.Google Scholar
Kadison, R. V., ‘Local derivations’, J. Algebra 130 (1990), 494–509.Google Scholar
Larson, D. R., ‘Reflexivity, algebraic reflexivity and linear interpretation’, Amer. J. Math. 110 (1988), 283–299.Google Scholar
Larson, D. R. and Sourour, A. R., ‘Local derivations and local automorphisms of B (X)’, in: Operator Theory: Operator Algebras and Applications, Part 2 (Durham, NH, 1988), Proceedings of Symposia in Pure Mathematics, 51 (American Mathematical Society, Providence, RI, 1990), 187–194.Google Scholar
Pisier, G., Similarity Problems and Completely Bounded Maps, 2nd expanded edn, Lecture Notes in Mathematics, 1618 (Springer, Berlin, 2001), includes the solution to ‘The Halmos problem’.Google Scholar
Samei, E., ‘Approximately local derivation’, J. Lond. Math. Soc. (2) 71(3) (2005), 759–778.10.1112/S0024610705006496Google Scholar
Samei, E., ‘Local properties of the Hochschild cohomology of C ∗ -algebras’, J. Aust. Math. Soc. 84 (2008), 117–130.Google Scholar
Samei, E., ‘Reflexivity and hyperreflexivity of bounded n-cocycles from group algebras’, Proc. Amer. Math. Soc. 139(1) (2011), 163–176.Google Scholar
Samei, E. and Soltani Farsani, J., ‘Hyperreflexivity of the bounded n-cocycle spaces of Banach algebras’, Monatsh. Math. 175(3) (2014), 429–455.Google Scholar
Sarason, D., ‘Invariant subspaces and unstarred operator algebras’, Pacific J. Math. 17 (1966), 511–517.Google Scholar
Shul’man, V. S., ‘Operators preserving ideals in C*-algebras’, Studia Math. 109 (1994), 67–72.Google Scholar