DISTALITY OF CERTAIN ACTIONS ON 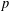$p$-ADIC SPHERES

Abstract

Consider the action of 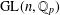$\operatorname{GL}(n,\mathbb{Q}_{p})$ on the 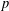$p$-adic unit sphere 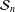${\mathcal{S}}_{n}$ arising from the linear action on 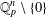$\mathbb{Q}_{p}^{n}\setminus \{0\}$. We show that for the action of a semigroup 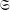$\mathfrak{S}$ of 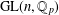$\operatorname{GL}(n,\mathbb{Q}_{p})$ on 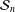${\mathcal{S}}_{n}$, the following are equivalent: (1) 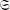$\mathfrak{S}$ acts distally on 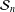${\mathcal{S}}_{n}$; (2) the closure of the image of 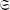$\mathfrak{S}$ in 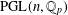$\operatorname{PGL}(n,\mathbb{Q}_{p})$ is a compact group. On 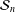${\mathcal{S}}_{n}$, we consider the ‘affine’ maps 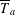$\overline{T}_{a}$ corresponding to 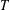$T$ in 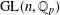$\operatorname{GL}(n,\mathbb{Q}_{p})$ and a nonzero $a$ in 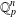$\mathbb{Q}_{p}^{n}$ satisfying 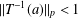$\Vert T^{-1}(a)\Vert _{p}<1$. We show that there exists a compact open subgroup 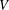$V$, which depends on 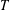$T$, such that 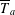$\overline{T}_{a}$ is distal for every nonzero 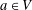$a\in V$ if and only if 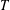$T$ acts distally on 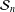${\mathcal{S}}_{n}$. The dynamics of ‘affine’ maps on 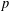$p$-adic unit spheres is quite different from that on the real unit spheres.