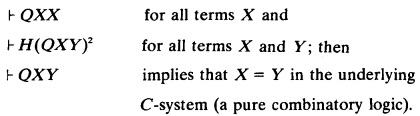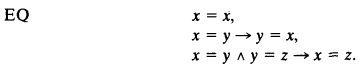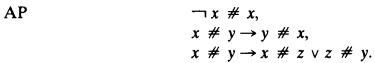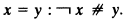Research Article
Maximal vector spaces under automorphisms of the lattice of recursively enumerable vector spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 481-491
-
- Article
- Export citation
Ordinal spectra of first-order theories1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 492-505
-
- Article
- Export citation
On the derivability of instantiation properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 506-514
-
- Article
- Export citation
Experimental logics and Π30 theories1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 515-522
-
- Article
- Export citation
Some consequences of an infinite-exponent partition relation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 523-526
-
- Article
- Export citation
Consistency notions in illative combinatory logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 527-529
-
- Article
- Export citation
On axiomatizing fragments
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 530-544
-
- Article
- Export citation
Computational complexity, speedable and levelable sets1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 545-563
-
- Article
- Export citation
An intuitionistically plausible interpretation of intuitionistic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 564-578
-
- Article
- Export citation
Reviews
Hao Wang. From mathematics to philosophy. International library of philosophy and scientific method. Humanities Press, New York1974, xiv + 428 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 579-580
-
- Article
- Export citation
J. Jay Zeman. Modal logic. The Lewis-modal systems. Clarendon Press, Oxford1973, x + 302 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 581
-
- Article
- Export citation
Daniel Gallin. Intensional and higher-order modal logic, with applications to Montague semantics. Mathematics studies, vol. 19. North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, ix + 148 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 581-583
-
- Article
- Export citation
Arto Salomaa. Formal languages. ACM monograph series. Academic Press, New York, San Francisco, and London, 1973, xiii + 322 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 583-584
-
- Article
- Export citation
Henry J. Ehlers. Logic: modern and traditional. Charles E. Merrill Publishing Company, Columbus, Ohio, 1976, viii + 245 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 584-585
-
- Article
- Export citation
George Boolos and Richard Jeffrey. Computability and logic. Cambridge University Press, New York and London1974, x + 262 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 585-586
-
- Article
- Export citation
J. N. Crossley and Anil Nerode. Combinatorial functors. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 81. Springer-Verlag, New York, Heidelberg, and Berlin, 1974, VIII + 146 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 586-587
-
- Article
- Export citation
Raymond Balbes and Philip Dwinger. Distributive lattices. University of Missouri Press, Columbia1974, xiii + 294 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 587-588
-
- Article
- Export citation
Alexander Abian. Boolean rings. Branden Press Publishers, Boston1976, ix + 394 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 588-589
-
- Article
- Export citation
Other
Association for Symbolic Logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 590-615
-
- Article
- Export citation
Index of Reviews
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 616-620
-
- Article
- Export citation

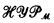 above a structure ℳ of urelements is to be found in Barwise's [75] book
above a structure ℳ of urelements is to be found in Barwise's [75] book 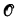 (ℳ). It coincides, for example, with Moschovakis' inductive closure ordinal over structures ℳ with pairing functions—and over some, such as algebraically closed fields of characteristic 0, without pairing functions (by recent work of Arthur Rubin) (although a locally famous counterexample of Kunen, a theorem of Barwise [77], and some recent results of Rubin and the author, show that the inductive closure ordinal may also be strictly smaller in suitably pathological structures). Further justification for looking at
(ℳ). It coincides, for example, with Moschovakis' inductive closure ordinal over structures ℳ with pairing functions—and over some, such as algebraically closed fields of characteristic 0, without pairing functions (by recent work of Arthur Rubin) (although a locally famous counterexample of Kunen, a theorem of Barwise [77], and some recent results of Rubin and the author, show that the inductive closure ordinal may also be strictly smaller in suitably pathological structures). Further justification for looking at 

 iff there is an experimental logic
iff there is an experimental logic  iff there is an experimental logic
iff there is an experimental logic  iff there is a convergent experimental logic
iff there is a convergent experimental logic 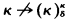 has a
has a 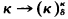 then
then  .
.