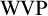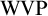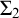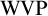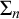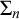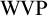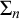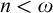1 Introduction
The Vopěnka Principle (
![]() $\mathrm {VP}$
), which asserts that there is no rigid proper class of graphs, is a well-known strong large-cardinal principleFootnote
1
(see [Reference Kanamori9]). Properly formulated as a first-order assertion,
$\mathrm {VP}$
), which asserts that there is no rigid proper class of graphs, is a well-known strong large-cardinal principleFootnote
1
(see [Reference Kanamori9]). Properly formulated as a first-order assertion,
![]() $\mathrm {VP}$
is a schema, that is, an infinite collection of statements, one for each first-order formula defining a proper class of graphs and asserting that the class defined by the formula is not rigid, i.e., there is some non-identity morphism. An equivalent formulation of
$\mathrm {VP}$
is a schema, that is, an infinite collection of statements, one for each first-order formula defining a proper class of graphs and asserting that the class defined by the formula is not rigid, i.e., there is some non-identity morphism. An equivalent formulation of
![]() $\mathrm {VP}$
as a first-order schema is given by restricting
$\mathrm {VP}$
as a first-order schema is given by restricting
![]() $\mathrm {VP}$
to proper classes of graphs that are definable with a certain degree of complexity, according to the Levy hierarchy of formulas
$\mathrm {VP}$
to proper classes of graphs that are definable with a certain degree of complexity, according to the Levy hierarchy of formulas
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $n<\omega $
(see [Reference Jech8]). Thus, writing
$n<\omega $
(see [Reference Jech8]). Thus, writing
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {VP}$
for the first-order assertion that every
$\mathrm {VP}$
for the first-order assertion that every
![]() $\Sigma _n$
-definable (with parameters) proper class of graphs is rigid, we have that
$\Sigma _n$
-definable (with parameters) proper class of graphs is rigid, we have that
![]() $\mathrm {VP}$
is equivalent to the schema consisting of
$\mathrm {VP}$
is equivalent to the schema consisting of
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {VP}$
for every n. As shown in [Reference Bagaria4, Reference Bagaria, Casacuberta, Mathias and Rosický5],
$\mathrm {VP}$
for every n. As shown in [Reference Bagaria4, Reference Bagaria, Casacuberta, Mathias and Rosický5],
![]() $\mathbf {\Sigma _1}$
-
$\mathbf {\Sigma _1}$
-
![]() $\mathrm {VP}$
is provable in ZFC, while
$\mathrm {VP}$
is provable in ZFC, while
![]() $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
![]() $\mathrm {VP}$
is equivalent to the existence of a proper class of supercompact cardinals,
$\mathrm {VP}$
is equivalent to the existence of a proper class of supercompact cardinals,
![]() $\mathbf {\Sigma _3}$
-
$\mathbf {\Sigma _3}$
-
![]() $\mathrm {VP}$
is equivalent to the existence of a proper class of extendible cardinals, and
$\mathrm {VP}$
is equivalent to the existence of a proper class of extendible cardinals, and
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {VP}$
is equivalent to the existence of a proper class of
$\mathrm {VP}$
is equivalent to the existence of a proper class of
![]() $C^{(n-2)}$
-extendible cardinals, for
$C^{(n-2)}$
-extendible cardinals, for
![]() $n\geq 3$
. The level-by-level analysis of
$n\geq 3$
. The level-by-level analysis of
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $n<\omega $
, and the determination of their large-cardinal strength yielded new results in category theory, homology theory, homotopy theory, and universal algebra (see [Reference Bagaria, Casacuberta, Mathias and Rosický5]). For example, the existence of cohomological localizations in the homotopy category of simplicial sets (Bousfield Conjecture) follows from
$n<\omega $
, and the determination of their large-cardinal strength yielded new results in category theory, homology theory, homotopy theory, and universal algebra (see [Reference Bagaria, Casacuberta, Mathias and Rosický5]). For example, the existence of cohomological localizations in the homotopy category of simplicial sets (Bousfield Conjecture) follows from
![]() $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
![]() $\mathrm {VP}$
.
$\mathrm {VP}$
.
The role of
![]() $\mathrm {VP}$
in category theory has a rich history. The first equivalences of
$\mathrm {VP}$
in category theory has a rich history. The first equivalences of
![]() $\mathrm {VP}$
with various category-theoretic statements were announced by Fisher in [Reference Fisher6]. Further equivalences were proved over the next two decades by Adámek, Rosický, Trnková, and others. Their work showed that under
$\mathrm {VP}$
with various category-theoretic statements were announced by Fisher in [Reference Fisher6]. Further equivalences were proved over the next two decades by Adámek, Rosický, Trnková, and others. Their work showed that under
![]() $\mathrm {VP}$
“the structure of locally presentable categories becomes much more transparent” [Reference Adámek and Rosický2, p. 241]. For example, the statement that a category is locally presentable if and only if it is complete and bounded is equivalent to
$\mathrm {VP}$
“the structure of locally presentable categories becomes much more transparent” [Reference Adámek and Rosický2, p. 241]. For example, the statement that a category is locally presentable if and only if it is complete and bounded is equivalent to
![]() $\mathrm {VP}$
. And so is the statement that every orthogonality class in a locally presentable category is a small-orthogonality class [Reference Adámek and Rosický2, 6.9 and 6.14], [Reference Rosický, Trnková and Adámek10]. Of the many category-theoretic statements now known to be equivalent to
$\mathrm {VP}$
. And so is the statement that every orthogonality class in a locally presentable category is a small-orthogonality class [Reference Adámek and Rosický2, 6.9 and 6.14], [Reference Rosický, Trnková and Adámek10]. Of the many category-theoretic statements now known to be equivalent to
![]() $\mathrm {VP}$
, the following one (see [Reference Adámek and Rosický2, 6.D]) turned out to be of particular interest:
$\mathrm {VP}$
, the following one (see [Reference Adámek and Rosický2, 6.D]) turned out to be of particular interest:
-
(1) Every full subcategory of a locally presentable category
 $\mathcal {K}$
closed under colimits is coreflective in
$\mathcal {K}$
closed under colimits is coreflective in
 $\mathcal {K}$
.
$\mathcal {K}$
.
What made (1) particularly interesting is that its dual statement
-
(2) Every full subcategory of a locally presentable category
 $\mathcal {K}$
closed under limits is reflective in
$\mathcal {K}$
closed under limits is reflective in
 $\mathcal {K}$
,
$\mathcal {K}$
,
while being a consequence of (1), could not be proved equivalent to it. Since
![]() $\mathrm {VP}$
—hence also (1)—was known to be equivalent to
$\mathrm {VP}$
—hence also (1)—was known to be equivalent to
(see [Reference Adámek and Rosický2, 6.3]), while statement (2) was proved equivalent to
(see [Reference Adámek and Rosický2, 6.22 and 6.23]), the latter assertion was then called the Weak Vopěnka Principle (WVP). The term Weak was aptly given, for it is readily shown that
![]() $\mathrm {VP}$
implies
$\mathrm {VP}$
implies
![]() $\mathrm {WVP}$
[Reference Adámek, Rosický, Trnková and Borceux3] (Proposition 2.1). The question then remained if
$\mathrm {WVP}$
[Reference Adámek, Rosický, Trnková and Borceux3] (Proposition 2.1). The question then remained if
![]() $\mathrm {WVP}$
implied
$\mathrm {WVP}$
implied
![]() $\mathrm {VP}$
. Using a result of Isbell [Reference Isbell7], which showed that
$\mathrm {VP}$
. Using a result of Isbell [Reference Isbell7], which showed that
![]() $\mathbf {Ord}^{\textit{op}}$
is bounded iff there is no proper class of measurable cardinals, Adámek and Rosický [Reference Adámek and Rosický2] proved that
$\mathbf {Ord}^{\textit{op}}$
is bounded iff there is no proper class of measurable cardinals, Adámek and Rosický [Reference Adámek and Rosický2] proved that
![]() $\mathrm {WVP}$
implies the existence of a proper class of measurable cardinals. This was seen as a first step in showing that
$\mathrm {WVP}$
implies the existence of a proper class of measurable cardinals. This was seen as a first step in showing that
![]() $\mathrm {WVP}$
was indeed a strong large-cardinal principle, perhaps even equivalent to
$\mathrm {WVP}$
was indeed a strong large-cardinal principle, perhaps even equivalent to
![]() $\mathrm {VP}$
. Much work was devoted to trying to obtain stronger large cardinals from it, e.g., strongly compact or supercompact cardinals, but to no avail. A further natural principle, between
$\mathrm {VP}$
. Much work was devoted to trying to obtain stronger large cardinals from it, e.g., strongly compact or supercompact cardinals, but to no avail. A further natural principle, between
![]() $\mathrm {VP}$
and
$\mathrm {VP}$
and
![]() $\mathrm {WVP}$
, called the Semi-Weak Vopěnka Principle (
$\mathrm {WVP}$
, called the Semi-Weak Vopěnka Principle (
![]() $\mathrm {SWVP}$
), was introduced in [Reference Adámek and Rosický1] and the further question of the equivalence between the three principles,
$\mathrm {SWVP}$
), was introduced in [Reference Adámek and Rosický1] and the further question of the equivalence between the three principles,
![]() $\mathrm {WVP}$
,
$\mathrm {WVP}$
,
![]() $\mathrm {SWVP}$
, and
$\mathrm {SWVP}$
, and
![]() $\mathrm {VP}$
, remained open. The problem was finally solved in 2019 by the second author of the present paper. In [Reference Wilson13] he showed that
$\mathrm {VP}$
, remained open. The problem was finally solved in 2019 by the second author of the present paper. In [Reference Wilson13] he showed that
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathrm {SWVP}$
are equivalent, and they are also equivalent to the large-cardinal principle “
$\mathrm {SWVP}$
are equivalent, and they are also equivalent to the large-cardinal principle “
![]() $\mathrm {OR}$
is Woodin,” whose consistency strength is known to be well below the existence of a supercompact cardinal, thereby showing that
$\mathrm {OR}$
is Woodin,” whose consistency strength is known to be well below the existence of a supercompact cardinal, thereby showing that
![]() $\mathrm {WVP}$
cannot imply
$\mathrm {WVP}$
cannot imply
![]() $\mathrm {VP}$
(if consistent with ZFC).
$\mathrm {VP}$
(if consistent with ZFC).
In the present paper we carry out a level-by-level analysis of
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathrm {SWVP}$
similar to the analysis of
$\mathrm {SWVP}$
similar to the analysis of
![]() $\mathrm {VP}$
done in [Reference Bagaria4, Reference Bagaria, Casacuberta, Mathias and Rosický5]. Thus, for every
$\mathrm {VP}$
done in [Reference Bagaria4, Reference Bagaria, Casacuberta, Mathias and Rosický5]. Thus, for every
![]() $n\geq 2$
we prove the equivalence of both
$n\geq 2$
we prove the equivalence of both
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {SWVP}$
(see Definition 2.2) with the existence of certain large cardinals. In particular, we show that
$\mathrm {SWVP}$
(see Definition 2.2) with the existence of certain large cardinals. In particular, we show that
![]() $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
![]() $\mathrm {SWVP}$
are equivalent to the existence of a proper class of strong cardinals. The main theorems (Theorems 5.11 and 5.13) show, more generally, that
$\mathrm {SWVP}$
are equivalent to the existence of a proper class of strong cardinals. The main theorems (Theorems 5.11 and 5.13) show, more generally, that
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {SWVP}$
are equivalent to the existence of a proper class of
$\mathrm {SWVP}$
are equivalent to the existence of a proper class of
![]() $\Sigma _n$
-strong cardinals (Definition 5.1). It follows that
$\Sigma _n$
-strong cardinals (Definition 5.1). It follows that
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathrm {SWVP}$
are equivalent to the schema asserting the existence of a
$\mathrm {SWVP}$
are equivalent to the schema asserting the existence of a
![]() $\Sigma _n$
-strong cardinal for every
$\Sigma _n$
-strong cardinal for every
![]() $n<\omega $
. Our arguments yield also a new proof of the second author’s result from [Reference Wilson13] that
$n<\omega $
. Our arguments yield also a new proof of the second author’s result from [Reference Wilson13] that
![]() $\mathrm {WVP}$
implies “
$\mathrm {WVP}$
implies “
![]() $\mathrm {OR}$
is Woodin” (Corollary 5.15). The main difference between the two proofs is that while in the present paper we derive the extenders witnessing “
$\mathrm {OR}$
is Woodin” (Corollary 5.15). The main difference between the two proofs is that while in the present paper we derive the extenders witnessing “
![]() $\mathrm {OR}$
is Woodin” from homomorphisms on products of relational structures with universe of the form
$\mathrm {OR}$
is Woodin” from homomorphisms on products of relational structures with universe of the form
![]() $V_\alpha $
, the proof in [Reference Wilson13] uses homomorphisms of so-called
$V_\alpha $
, the proof in [Reference Wilson13] uses homomorphisms of so-called
![]() $\mathcal {P}$
-structures. We think, however, that it should be possible to do a similar level-by-level analysis as done here by using
$\mathcal {P}$
-structures. We think, however, that it should be possible to do a similar level-by-level analysis as done here by using
![]() $\mathcal {P}$
-structures instead. A number of consequences in category theory should follow from our results. For instance, the statement that every
$\mathcal {P}$
-structures instead. A number of consequences in category theory should follow from our results. For instance, the statement that every
![]() $\mathbf {\Sigma _2}$
-definable full subcategory of a locally presentable category
$\mathbf {\Sigma _2}$
-definable full subcategory of a locally presentable category
![]() $\mathcal {K}$
closed in
$\mathcal {K}$
closed in
![]() $\mathcal {K}$
under limits is reflective in
$\mathcal {K}$
under limits is reflective in
![]() $\mathcal {K}$
, should be equivalent to the existence of a proper class of strong cardinals. See [Reference Adámek and Rosický2, Chapter 6] for more examples.
$\mathcal {K}$
, should be equivalent to the existence of a proper class of strong cardinals. See [Reference Adámek and Rosický2, Chapter 6] for more examples.
2 Preliminaries
Recall that a graph is a structure
![]() $G=\langle G, E_G\rangle $
, where G is a non-empty set and
$G=\langle G, E_G\rangle $
, where G is a non-empty set and
![]() $E_G$
is a binary relation on G. If
$E_G$
is a binary relation on G. If
![]() $G=\langle G, E_G\rangle $
and
$G=\langle G, E_G\rangle $
and
![]() $H=\langle H, E_H\rangle $
are graphs, a map
$H=\langle H, E_H\rangle $
are graphs, a map
![]() $h:G\to H$
is a homomorphism if it preserves the binary relation, meaning that for all
$h:G\to H$
is a homomorphism if it preserves the binary relation, meaning that for all
![]() $x,y\in G$
, if
$x,y\in G$
, if
![]() $xE_G y$
, then
$xE_G y$
, then
![]() $h(x)E_H h(y)$
.
$h(x)E_H h(y)$
.
A class
![]() $\mathcal {G}$
of graphs is called rigid if there are no non-trivial homomorphisms between graphs in
$\mathcal {G}$
of graphs is called rigid if there are no non-trivial homomorphisms between graphs in
![]() $\mathcal {G}$
, i.e., the only homomorphisms are the identity morphisms
$\mathcal {G}$
, i.e., the only homomorphisms are the identity morphisms
![]() $G\to G$
, for
$G\to G$
, for
![]() $G\in \mathcal {G}$
.
$G\in \mathcal {G}$
.
The original formulation of the Vopěnka Principle (
![]() $\mathrm {VP}$
) (P. Vopěnka, ca. 1960) asserts that there is no rigid proper class of graphs. As shown in [Reference Adámek and Rosický2, 6.A],
$\mathrm {VP}$
) (P. Vopěnka, ca. 1960) asserts that there is no rigid proper class of graphs. As shown in [Reference Adámek and Rosický2, 6.A],
![]() $\mathrm {VP}$
is equivalent to the statement that the category
$\mathrm {VP}$
is equivalent to the statement that the category
![]() $\mathbf {Ord}$
of ordinals cannot be fully embedded into the category
$\mathbf {Ord}$
of ordinals cannot be fully embedded into the category
![]() $\mathbf {Gra}$
of graphs. That is, there is no sequence
$\mathbf {Gra}$
of graphs. That is, there is no sequence
![]() $\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
$\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
![]() $\alpha \leq \beta $
there exists exactly one homomorphism
$\alpha \leq \beta $
there exists exactly one homomorphism
![]() $G_\alpha \to G_\beta $
, and no homomorphism
$G_\alpha \to G_\beta $
, and no homomorphism
![]() $G_\beta \to G_\alpha $
whenever
$G_\beta \to G_\alpha $
whenever
![]() $\alpha < \beta $
.
$\alpha < \beta $
.
The Weak Vopěnka Principle (
![]() $\mathrm {WVP}$
) (first introduced in [Reference Adámek, Rosický, Trnková and Borceux3]) is the statement dual to
$\mathrm {WVP}$
) (first introduced in [Reference Adámek, Rosický, Trnková and Borceux3]) is the statement dual to
![]() $\mathrm {VP}$
, namely that the opposite category of ordinals,
$\mathrm {VP}$
, namely that the opposite category of ordinals,
![]() $\mathbf {Ord}^{\textit{op}}$
, cannot be fully embedded into
$\mathbf {Ord}^{\textit{op}}$
, cannot be fully embedded into
![]() $\mathbf {Gra}$
. That is, there is no sequence
$\mathbf {Gra}$
. That is, there is no sequence
![]() $\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
$\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
![]() $\alpha \leq \beta $
there exists exactly one homomorphism
$\alpha \leq \beta $
there exists exactly one homomorphism
![]() $G_\beta \to G_\alpha $
, and no homomorphism
$G_\beta \to G_\alpha $
, and no homomorphism
![]() $G_\alpha \to G_\beta $
whenever
$G_\alpha \to G_\beta $
whenever
![]() $\alpha < \beta $
.
$\alpha < \beta $
.
The Semi-Weak Vopěnka Principle (
![]() $\mathrm {SWVP}$
) [Reference Adámek and Rosický1] asserts that there is no sequence
$\mathrm {SWVP}$
) [Reference Adámek and Rosický1] asserts that there is no sequence
![]() $\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
$\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
![]() $\alpha \leq \beta $
there exists some (not necessarily unique) homomorphism
$\alpha \leq \beta $
there exists some (not necessarily unique) homomorphism
![]() $G_\beta \to G_\alpha $
, and no homomorphism
$G_\beta \to G_\alpha $
, and no homomorphism
![]() $G_\alpha \to G_\beta $
whenever
$G_\alpha \to G_\beta $
whenever
![]() $\alpha < \beta $
.
$\alpha < \beta $
.
Clearly,
![]() $\mathrm {SWVP}$
implies
$\mathrm {SWVP}$
implies
![]() $\mathrm {WVP}$
. The second author showed in [Reference Wilson12] that
$\mathrm {WVP}$
. The second author showed in [Reference Wilson12] that
![]() $\mathrm {SWVP}$
is in fact equivalent to
$\mathrm {SWVP}$
is in fact equivalent to
![]() $\mathrm {WVP}$
. As shown in [Reference Adámek, Rosický, Trnková and Borceux3],
$\mathrm {WVP}$
. As shown in [Reference Adámek, Rosický, Trnková and Borceux3],
![]() $\mathrm {VP}$
implies
$\mathrm {VP}$
implies
![]() $\mathrm {WVP}$
, and the same argument also shows that
$\mathrm {WVP}$
, and the same argument also shows that
![]() $\mathrm {VP}$
implies
$\mathrm {VP}$
implies
![]() $\mathrm {SWVP}$
. In fact, the argument shows the following:
$\mathrm {SWVP}$
. In fact, the argument shows the following:
Proposition 2.1.
![]() $\mathrm {VP}$
implies that for every sequence
$\mathrm {VP}$
implies that for every sequence
![]() $\langle G_\alpha : \alpha \in \mathrm {OR} \rangle $
of graphs there exist
$\langle G_\alpha : \alpha \in \mathrm {OR} \rangle $
of graphs there exist
![]() $\alpha <\beta $
with a homomorphism
$\alpha <\beta $
with a homomorphism
![]() $G_\alpha \to G_\beta $
.
$G_\alpha \to G_\beta $
.
Proof Suppose
![]() $\langle G_\alpha : \alpha \in \mathrm {OR} \rangle $
is a sequence of graphs. Without loss of generality, if
$\langle G_\alpha : \alpha \in \mathrm {OR} \rangle $
is a sequence of graphs. Without loss of generality, if
![]() $\alpha < \beta $
, then
$\alpha < \beta $
, then
![]() $G_\alpha $
and
$G_\alpha $
and
![]() $G_\beta $
are not isomorphic. Since there are only set-many (as opposed to proper-class-many) non-isomorphic graphs of any given cardinality, there exists a proper class
$G_\beta $
are not isomorphic. Since there are only set-many (as opposed to proper-class-many) non-isomorphic graphs of any given cardinality, there exists a proper class
![]() $C\subseteq \mathrm {OR}$
such that
$C\subseteq \mathrm {OR}$
such that
![]() $|G_\alpha | <|G_\beta |$
whenever
$|G_\alpha | <|G_\beta |$
whenever
![]() $\alpha <\beta $
are in C. For each
$\alpha <\beta $
are in C. For each
![]() $\alpha \in C$
, add to
$\alpha \in C$
, add to
![]() $G_\alpha =\langle G_\alpha , E_\alpha \rangle $
a rigid binary relation
$G_\alpha =\langle G_\alpha , E_\alpha \rangle $
a rigid binary relation
![]() $S_\alpha $
on
$S_\alpha $
on
![]() $G_\alpha $
[Reference Vopěnka, Pultr and Hedrlín11], as well as the non-identity relation
$G_\alpha $
[Reference Vopěnka, Pultr and Hedrlín11], as well as the non-identity relation
![]() $\not =$
, and consider the structure
$\not =$
, and consider the structure
![]() $A_\alpha =\langle G_\alpha , E_\alpha , S_\alpha , \not =\rangle $
. Since the cardinalities are strictly increasing, by the
$A_\alpha =\langle G_\alpha , E_\alpha , S_\alpha , \not =\rangle $
. Since the cardinalities are strictly increasing, by the
![]() $\not =$
relation there cannot be any homomorphism
$\not =$
relation there cannot be any homomorphism
![]() $A_\beta \to A_\alpha $
with
$A_\beta \to A_\alpha $
with
![]() $\alpha <\beta $
. Also, because of the rigid relation
$\alpha <\beta $
. Also, because of the rigid relation
![]() $S_\alpha $
, the identity is the only homomorphism
$S_\alpha $
, the identity is the only homomorphism
![]() $A_\alpha \to A_\alpha $
. Since the category whose objects are the
$A_\alpha \to A_\alpha $
. Since the category whose objects are the
![]() $A_\alpha $
,
$A_\alpha $
,
![]() $\alpha \in C$
and the morphisms are the homomorphisms can be fully embedded into
$\alpha \in C$
and the morphisms are the homomorphisms can be fully embedded into
![]() $\mathbf {Gra}$
(see [Reference Adámek and Rosický2, 2.65]), by
$\mathbf {Gra}$
(see [Reference Adámek and Rosický2, 2.65]), by
![]() $\mathrm {VP}$
the class
$\mathrm {VP}$
the class
![]() $\{ A_\alpha :\alpha \in C\}$
is not rigid, and so there must exist
$\{ A_\alpha :\alpha \in C\}$
is not rigid, and so there must exist
![]() $\alpha <\beta $
with a homomorphism
$\alpha <\beta $
with a homomorphism
![]() $A_\alpha \to A_\beta $
, hence also a homomorphism
$A_\alpha \to A_\beta $
, hence also a homomorphism
![]() $G_\alpha \to G_\beta $
.
$G_\alpha \to G_\beta $
.
The definitions of
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\mathrm {SWVP}$
given above quantify over arbitrary classes, so they are not first-order. Thus, a proper study of these principles must be carried out in some adequate class theory, such as NBG. In particular, the proof of the last proposition can only be formally given in such class theory. We shall however be interested in the forthcoming in the first-order versions of
$\mathrm {SWVP}$
given above quantify over arbitrary classes, so they are not first-order. Thus, a proper study of these principles must be carried out in some adequate class theory, such as NBG. In particular, the proof of the last proposition can only be formally given in such class theory. We shall however be interested in the forthcoming in the first-order versions of
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\mathrm {SWVP}$
, which require us to restrict our attention to definable classes.
$\mathrm {SWVP}$
, which require us to restrict our attention to definable classes.
2.1 The VP, WVP, and SWVP for definable classes
Each of
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\mathrm {SWVP}$
can be formulated in the first-order language of set theory as a definition schema, namely as an infinite list of definitions, one for every natural number n, as follows:
$\mathrm {SWVP}$
can be formulated in the first-order language of set theory as a definition schema, namely as an infinite list of definitions, one for every natural number n, as follows:
Definition 2.2. Let n be a natural number, and let P be a set or a proper class.
The
![]() $\Sigma _n(P)$
-Vopěnka Principle (
$\Sigma _n(P)$
-Vopěnka Principle (
![]() $\Sigma _n(P)$
-
$\Sigma _n(P)$
-
![]() $\mathrm {VP}$
for short) asserts that there is no
$\mathrm {VP}$
for short) asserts that there is no
![]() $\Sigma _n$
-definable, with parameters in P, sequence
$\Sigma _n$
-definable, with parameters in P, sequence
![]() $\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
$\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
![]() $\alpha \leq \beta $
there exists exactly one homomorphism
$\alpha \leq \beta $
there exists exactly one homomorphism
![]() $G_\alpha \to G_\beta $
, and no homomorphism
$G_\alpha \to G_\beta $
, and no homomorphism
![]() $G_\beta \to G_\alpha $
whenever
$G_\beta \to G_\alpha $
whenever
![]() $\alpha <\beta $
.
$\alpha <\beta $
.
The
![]() $\Sigma _n(P)$
-Weak Vopěnka Principle (
$\Sigma _n(P)$
-Weak Vopěnka Principle (
![]() $\Sigma _n(P)$
-
$\Sigma _n(P)$
-
![]() $\mathrm {WVP}$
for short) asserts that there is no
$\mathrm {WVP}$
for short) asserts that there is no
![]() $\Sigma _n$
-definable, with parameters in P, sequence
$\Sigma _n$
-definable, with parameters in P, sequence
![]() $\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
$\langle G_\alpha :\alpha \in \mathrm {OR}\rangle $
of graphs such that for every
![]() $\alpha \leq \beta $
there exists exactly one homomorphism
$\alpha \leq \beta $
there exists exactly one homomorphism
![]() $G_\beta \to G_\alpha $
, and no homomorphism
$G_\beta \to G_\alpha $
, and no homomorphism
![]() $G_\alpha \to G_\beta $
whenever
$G_\alpha \to G_\beta $
whenever
![]() $\alpha <\beta $
.
$\alpha <\beta $
.
The boldface versions
![]() ${\mathbf \Sigma _n}$
-
${\mathbf \Sigma _n}$
-
![]() $\mathrm {VP}$
and
$\mathrm {VP}$
and
![]() ${\mathbf \Sigma _n}$
-
${\mathbf \Sigma _n}$
-
![]() $\mathrm {WVP}$
are defined as
$\mathrm {WVP}$
are defined as
![]() $\Sigma _n(V)$
-
$\Sigma _n(V)$
-
![]() $\mathrm {VP}$
and
$\mathrm {VP}$
and
![]() $\Sigma _n(V)$
-
$\Sigma _n(V)$
-
![]() $\mathrm {WVP}$
respectively, i.e., any set is allowed as a parameter in the definitions.
$\mathrm {WVP}$
respectively, i.e., any set is allowed as a parameter in the definitions.
![]() $\Pi _n(P)$
-
$\Pi _n(P)$
-
![]() $\mathrm {VP}$
and
$\mathrm {VP}$
and
![]() $\Pi _n(P)$
-
$\Pi _n(P)$
-
![]() $\mathrm {WVP}$
, as well as
$\mathrm {WVP}$
, as well as
![]() $\mathbf {\Pi _n}$
-
$\mathbf {\Pi _n}$
-
![]() $\mathrm {VP}$
and
$\mathrm {VP}$
and
![]() $\mathbf {\Pi _n}$
-
$\mathbf {\Pi _n}$
-
![]() $\mathrm {WVP}$
, and the lightface (i.e., without parameters) versions
$\mathrm {WVP}$
, and the lightface (i.e., without parameters) versions
![]() $\Sigma _n$
-
$\Sigma _n$
-
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\Sigma _n$
-
$\Sigma _n$
-
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\Pi _n$
-
$\Pi _n$
-
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\Pi _n$
-
$\Pi _n$
-
![]() $\mathrm {WVP}$
, are defined similarly.
$\mathrm {WVP}$
, are defined similarly.
The Vopěnka Principle (
![]() $\mathrm {VP}$
) is the schema asserting that the
$\mathrm {VP}$
) is the schema asserting that the
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {VP}$
holds for every
$\mathrm {VP}$
holds for every
![]() $n < \omega $
. And the Weak Vopěnka Principle (
$n < \omega $
. And the Weak Vopěnka Principle (
![]() $\mathrm {WVP}$
) is the schema asserting that the
$\mathrm {WVP}$
) is the schema asserting that the
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {WVP}$
holds for every
$\mathrm {WVP}$
holds for every
![]() $n < \omega $
.
$n < \omega $
.
If instead of requiring that for
![]() $\alpha \leq \beta $
there is exactly one homomorphism
$\alpha \leq \beta $
there is exactly one homomorphism
![]() ${G_\beta \to G_\alpha }$
we only require that there is at least one, then we obtain the Semi-Weak Vopěnka Principle (
${G_\beta \to G_\alpha }$
we only require that there is at least one, then we obtain the Semi-Weak Vopěnka Principle (
![]() $\mathrm {SWVP}$
), formulated as the first-order schema consisting of
$\mathrm {SWVP}$
), formulated as the first-order schema consisting of
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {SWVP}$
for all
$\mathrm {SWVP}$
for all
![]() $n<\omega $
.
$n<\omega $
.
It is well-known that the category of structures in any fixed (many-sorted, infinitary) relational language can be fully embedded into
![]() $\mathbf {Gra}$
(see [Reference Adámek and Rosický2, 2.65]). Thus, if in the original definitions of
$\mathbf {Gra}$
(see [Reference Adámek and Rosický2, 2.65]). Thus, if in the original definitions of
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\mathrm {SWVP}$
one replaces “graphs” by “structures in a fixed (many-sorted, infinitary) relational language,” one obtains equivalent notions. The same is true for the first-order formulations of these principles, but some extra care is needed to ensure there is no increase in the complexity of the definitions. In particular, in the case of infinite language signatures, an extra parameter for the language signature
$\mathrm {SWVP}$
one replaces “graphs” by “structures in a fixed (many-sorted, infinitary) relational language,” one obtains equivalent notions. The same is true for the first-order formulations of these principles, but some extra care is needed to ensure there is no increase in the complexity of the definitions. In particular, in the case of infinite language signatures, an extra parameter for the language signature
![]() $\tau $
, as well as a parameter for a rigid binary relation on a binary signature associated with
$\tau $
, as well as a parameter for a rigid binary relation on a binary signature associated with
![]() $\tau $
, may be needed in the definition. Namely, suppose
$\tau $
, may be needed in the definition. Namely, suppose
![]() $\Gamma $
is one of the definability classes
$\Gamma $
is one of the definability classes
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $\Pi _n$
, with
$\Pi _n$
, with
![]() $n\geq 1$
, P is a set or a proper class, and
$n\geq 1$
, P is a set or a proper class, and
![]() ${\mathcal C}$
is a
${\mathcal C}$
is a
![]() $\Gamma $
-definable, with parameters in P, class of (possibly many-sorted) relational structures in a language type
$\Gamma $
-definable, with parameters in P, class of (possibly many-sorted) relational structures in a language type
![]() $\tau $
, i.e.,
$\tau $
, i.e.,
![]() $\tau =\langle R_\alpha :\alpha <\lambda \rangle $
, where each
$\tau =\langle R_\alpha :\alpha <\lambda \rangle $
, where each
![]() $R_\alpha $
is an
$R_\alpha $
is an
![]() $n_\alpha $
-ary relation symbol,
$n_\alpha $
-ary relation symbol,
![]() $n_\alpha $
being some ordinal, possibly infinite. As in [Reference Adámek and Rosický2, 2.65], there is a
$n_\alpha $
being some ordinal, possibly infinite. As in [Reference Adámek and Rosický2, 2.65], there is a
![]() $\Delta _1$
-definable (i.e., both
$\Delta _1$
-definable (i.e., both
![]() $\Sigma _1$
-definable and
$\Sigma _1$
-definable and
![]() $\Pi _1$
-definable), using
$\Pi _1$
-definable), using
![]() $\tau $
as a parameter, one-sorted binary type
$\tau $
as a parameter, one-sorted binary type
![]() $\tau '$
(meaning that all the relations are binary), and also a
$\tau '$
(meaning that all the relations are binary), and also a
![]() $\Gamma $
-definable, with parameters in P plus
$\Gamma $
-definable, with parameters in P plus
![]() $\tau $
as an additional parameter, full embedding of
$\tau $
as an additional parameter, full embedding of
![]() ${\mathcal C}$
into the category
${\mathcal C}$
into the category
![]() $\mathbf {Rel} \, \tau '$
of
$\mathbf {Rel} \, \tau '$
of
![]() $\tau '$
-structures and homomorphisms. Furthermore, there is a
$\tau '$
-structures and homomorphisms. Furthermore, there is a
![]() $\Delta _1$
-definable, using
$\Delta _1$
-definable, using
![]() $\tau $
and a rigid binary relation r on
$\tau $
and a rigid binary relation r on
![]() $\tau '$
as parameters, full embedding of
$\tau '$
as parameters, full embedding of
![]() $\mathbf {Rel} \, \tau '$
into
$\mathbf {Rel} \, \tau '$
into
![]() $\mathbf {Gra}$
. Hence, there is a
$\mathbf {Gra}$
. Hence, there is a
![]() $\Gamma $
-definable (with parameters in P, plus
$\Gamma $
-definable (with parameters in P, plus
![]() $\tau $
and r as additional parameters) full embedding of
$\tau $
and r as additional parameters) full embedding of
![]() ${\mathcal C}$
into
${\mathcal C}$
into
![]() $\mathbf {Gra}$
. Therefore, in the definitions of
$\mathbf {Gra}$
. Therefore, in the definitions of
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {SWVP}$
we may replace “graphs” by “structures in a fixed (many-sorted, infinitary) relational language” and obtain equivalent principles, provided we allow for the additional parameters (
$\mathrm {SWVP}$
we may replace “graphs” by “structures in a fixed (many-sorted, infinitary) relational language” and obtain equivalent principles, provided we allow for the additional parameters (
![]() $\tau $
and r) involved. Let us, however, stress the fact that in the case of finite
$\tau $
and r) involved. Let us, however, stress the fact that in the case of finite
![]() $\tau $
, or even if
$\tau $
, or even if
![]() $\tau $
is countable infinite and definable without parameters (e.g., recursive), then no additional parameters are involved, and therefore the versions of
$\tau $
is countable infinite and definable without parameters (e.g., recursive), then no additional parameters are involved, and therefore the versions of
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {VP}$
,
$\mathrm {VP}$
,
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {WVP}$
, and
$\mathrm {WVP}$
, and
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {SWVP}$
for graphs and for relational structures are equivalent.
$\mathrm {SWVP}$
for graphs and for relational structures are equivalent.
2.2 Strong cardinals
Recall that a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-strong, where
$\lambda $
-strong, where
![]() $\lambda $
is a cardinal greater than
$\lambda $
is a cardinal greater than
![]() $\kappa $
, if there exists an elementary embedding
$\kappa $
, if there exists an elementary embedding
![]() $j: V\to M$
, with M transitive, with critical point
$j: V\to M$
, with M transitive, with critical point
![]() $\kappa $
, and with
$\kappa $
, and with
![]() $V_\lambda $
contained in M. A cardinal
$V_\lambda $
contained in M. A cardinal
![]() $\kappa $
is strong if it is
$\kappa $
is strong if it is
![]() $\lambda $
-strong for every cardinal
$\lambda $
-strong for every cardinal
![]() $\lambda>\kappa $
.
$\lambda>\kappa $
.
If
![]() $\kappa $
is a strong cardinal, then for every cardinal
$\kappa $
is a strong cardinal, then for every cardinal
![]() $\lambda>\kappa $
there exists an elementary embedding
$\lambda>\kappa $
there exists an elementary embedding
![]() $j: V\to M$
, with M transitive, critical point
$j: V\to M$
, with M transitive, critical point
![]() $\kappa $
,
$\kappa $
,
![]() $V_\lambda $
contained in M, and
$V_\lambda $
contained in M, and
![]() $j(\kappa )>\lambda $
. Moreover, if
$j(\kappa )>\lambda $
. Moreover, if
![]() $\kappa $
is strong, then
$\kappa $
is strong, then
![]() $V_\kappa \preceq _{\Sigma _2}V$
. (See [Reference Kanamori9].)
$V_\kappa \preceq _{\Sigma _2}V$
. (See [Reference Kanamori9].)
It is well-known that the notion of strong cardinal can be formulated in terms of extenders (see [Reference Kanamori9, Section 26]). Namely,
Definition 2.3. Given a cardinal
![]() $\kappa $
, and
$\kappa $
, and
![]() $\beta>\kappa $
, a
$\beta>\kappa $
, a
![]() $(\kappa ,\beta )$
-extender is a collection
$(\kappa ,\beta )$
-extender is a collection
![]() ${\mathcal E}:=\{ E_a:a\in [\beta ]^{<\omega }\}$
such that:
${\mathcal E}:=\{ E_a:a\in [\beta ]^{<\omega }\}$
such that:
-
(1) Each
 $E_a$
is a
$E_a$
is a
 $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
 $[\kappa ]^{|a|}$
, and
$[\kappa ]^{|a|}$
, and
 $E_{a}$
is not
$E_{a}$
is not
 $\kappa ^+$
-complete for some a.
$\kappa ^+$
-complete for some a. -
(2) For each
 $\xi <\kappa $
, there is some a with
$\xi <\kappa $
, there is some a with
 $\{ s\in [\kappa ]^{|a|}:\xi \in s\}\in E_a$
.
$\{ s\in [\kappa ]^{|a|}:\xi \in s\}\in E_a$
. -
(3) Coherence: If
 $a\subseteq b$
are in
$a\subseteq b$
are in
 $[\beta ]^{<\omega }$
, with
$[\beta ]^{<\omega }$
, with
 $b=\{ \alpha _1,\ldots , \alpha _n\}$
and
$b=\{ \alpha _1,\ldots , \alpha _n\}$
and
 $a=\{ \alpha _{i_1}, \ldots , \alpha _{i_n}\}$
, and
$a=\{ \alpha _{i_1}, \ldots , \alpha _{i_n}\}$
, and
 $\pi _{ba}:[\kappa ]^{|b|}\to [\kappa ]^{|a|}$
is the map given by
$\pi _{ba}:[\kappa ]^{|b|}\to [\kappa ]^{|a|}$
is the map given by
 $\pi _{ba}(\{ \xi _1,\ldots ,\xi _n\})=\{ \xi _{i_1},\ldots ,\xi _{i_n}\}$
, then
$\pi _{ba}(\{ \xi _1,\ldots ,\xi _n\})=\{ \xi _{i_1},\ldots ,\xi _{i_n}\}$
, then  $$ \begin{align*}X\in E_a \quad \mbox{ if and only if } \quad \{ s\in [\kappa]^{|b|}: \pi_{ba}(s)\in X\}\in E_b\, .\end{align*} $$
$$ \begin{align*}X\in E_a \quad \mbox{ if and only if } \quad \{ s\in [\kappa]^{|b|}: \pi_{ba}(s)\in X\}\in E_b\, .\end{align*} $$
-
(4) Normality: Whenever
 $a\in [\beta ]^{<\omega }$
and
$a\in [\beta ]^{<\omega }$
and
 $f:[\kappa ]^{|a|} \to V$
are such that
$f:[\kappa ]^{|a|} \to V$
are such that
 $\{ s\in [\kappa ]^{|a|}: f(s)\in {\mathrm {max}}(s)\}\in E_a$
, there is
$\{ s\in [\kappa ]^{|a|}: f(s)\in {\mathrm {max}}(s)\}\in E_a$
, there is
 $b\in [\beta ]^{<\omega }$
with
$b\in [\beta ]^{<\omega }$
with
 $a\subseteq b$
such that
$a\subseteq b$
such that  $$ \begin{align*}\{ s\in [\kappa]^{|b|}: f(\pi_{ba}(s))\in s\}\in E_{b}\, .\end{align*} $$
$$ \begin{align*}\{ s\in [\kappa]^{|b|}: f(\pi_{ba}(s))\in s\}\in E_{b}\, .\end{align*} $$
-
(5) Well-foundedness: Whenever
 $a_m\in [\beta ]^{<\omega }$
and
$a_m\in [\beta ]^{<\omega }$
and
 $X_m\in E_{a_m}$
for
$X_m\in E_{a_m}$
for
 $m\in \omega $
, there is a function
$m\in \omega $
, there is a function
 $d:\bigcup _m a_m \to \kappa $
such that
$d:\bigcup _m a_m \to \kappa $
such that
 $d“ a_m \in X_m$
for every m.
$d“ a_m \in X_m$
for every m.
Proposition 2.4. A cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-strong if and only if there exists a
$\lambda $
-strong if and only if there exists a
![]() $(\kappa , |V_{\lambda }|^+)$
-extender
$(\kappa , |V_{\lambda }|^+)$
-extender
![]() $\mathcal {E}$
such that
$\mathcal {E}$
such that
![]() $V_{\lambda }\subseteq \overline {M}_{\mathcal {E}}$
and
$V_{\lambda }\subseteq \overline {M}_{\mathcal {E}}$
and
![]() $\lambda <j_{\mathcal {E}}(\kappa )$
(where
$\lambda <j_{\mathcal {E}}(\kappa )$
(where
![]() $\overline {M}_{\mathcal {E}}$
is the transitive collapse of the direct limit ultrapower
$\overline {M}_{\mathcal {E}}$
is the transitive collapse of the direct limit ultrapower
![]() $M_{\mathcal {E}}$
of V by
$M_{\mathcal {E}}$
of V by
![]() $\mathcal {E}$
, and
$\mathcal {E}$
, and
![]() $j_{\mathcal {E}}:V\to \overline {M}_{\mathcal {E}}$
is the corresponding elementary embedding).
$j_{\mathcal {E}}:V\to \overline {M}_{\mathcal {E}}$
is the corresponding elementary embedding).
Proof See [Reference Kanamori9, Exercise 26.7].
3 The Product Reflection Principle
For any set S of relational structures
![]() $\mathcal {A}=\langle A, \ldots \rangle $
of the same type, the set-theoretic product
$\mathcal {A}=\langle A, \ldots \rangle $
of the same type, the set-theoretic product
![]() $\prod S$
is the structure whose universe is the set of all functions f with domain S such that
$\prod S$
is the structure whose universe is the set of all functions f with domain S such that
![]() $f(\mathcal {A})\in A$
for every
$f(\mathcal {A})\in A$
for every
![]() $\mathcal {A}\in S$
, and whose relations are defined pointwise.
$\mathcal {A}\in S$
, and whose relations are defined pointwise.
Definition 3.1 (The Product Reflection Principle (
 $\mathrm {PRP}$
))
$\mathrm {PRP}$
))
For
![]() $\Gamma $
a definability class (i.e., one of
$\Gamma $
a definability class (i.e., one of
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $\Pi _n$
, some
$\Pi _n$
, some
![]() $n>0$
), and P a set or proper class,
$n>0$
), and P a set or proper class,
![]() $\Gamma (P)$
-
$\Gamma (P)$
-
![]() $\mathrm {PRP}$
asserts that for every class
$\mathrm {PRP}$
asserts that for every class
![]() ${\mathcal C}$
of graphs that is
${\mathcal C}$
of graphs that is
![]() $\Gamma $
-definable with parameters in P, the following holds:
$\Gamma $
-definable with parameters in P, the following holds:
-
PRP: There is a non-empty subset S of
 ${\mathcal C}$
such that for every G in
${\mathcal C}$
such that for every G in
 ${\mathcal C}$
there is a homomorphism
${\mathcal C}$
there is a homomorphism
 $\prod S \to G$
.
$\prod S \to G$
.
If
![]() $P=\varnothing $
, then we simply write
$P=\varnothing $
, then we simply write
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {PRP}$
. If
$\mathrm {PRP}$
. If
![]() $P=V$
, then we write
$P=V$
, then we write
![]() $\Gamma $
in boldface, e.g.,
$\Gamma $
in boldface, e.g.,
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {PRP}$
.
$\mathrm {PRP}$
.
Note that in the case where
![]() ${\mathcal C}$
is a set, PRP is trivial because we may take
${\mathcal C}$
is a set, PRP is trivial because we may take
![]() $S = {\mathcal C}$
and use the coordinate projection homomorphisms from
$S = {\mathcal C}$
and use the coordinate projection homomorphisms from
![]() $\prod S$
, so the nontrivial case is the one where
$\prod S$
, so the nontrivial case is the one where
![]() ${\mathcal C}$
is a proper class (and S is still required to be a set.)
${\mathcal C}$
is a proper class (and S is still required to be a set.)
In the definition of
![]() $\Gamma (P)$
-
$\Gamma (P)$
-
![]() $\mathrm {PRP}$
we may replace “graphs” by “structures in a fixed (many-sorted, infinitary) relational language” and obtain equivalent principles, provided we allow for some additional parameters (see our remarks after Definition 2.2). Thus, the boldface principle
$\mathrm {PRP}$
we may replace “graphs” by “structures in a fixed (many-sorted, infinitary) relational language” and obtain equivalent principles, provided we allow for some additional parameters (see our remarks after Definition 2.2). Thus, the boldface principle
![]() $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
![]() $\mathrm {PRP}$
for classes of graphs is equivalent to its version for classes of relational structures.
$\mathrm {PRP}$
for classes of graphs is equivalent to its version for classes of relational structures.
We shall denote by
![]() $C^{(n)}$
the
$C^{(n)}$
the
![]() $\Pi _n$
-definable closed and unbounded class of ordinals
$\Pi _n$
-definable closed and unbounded class of ordinals
![]() $\kappa $
that are
$\kappa $
that are
![]() $\Sigma _n$
-correct in V, i.e.,
$\Sigma _n$
-correct in V, i.e.,
![]() $V_\kappa \preceq _{\Sigma _n}V$
. (See [Reference Bagaria4].)
$V_\kappa \preceq _{\Sigma _n}V$
. (See [Reference Bagaria4].)
Proposition 3.2.
![]() $\mathbf {\Sigma _1}$
-
$\mathbf {\Sigma _1}$
-
![]() $\mathrm {PRP}$
holds. In fact, for every
$\mathrm {PRP}$
holds. In fact, for every
![]() $\kappa \in C^{(1)}$
and every
$\kappa \in C^{(1)}$
and every
![]() $\Sigma _1$
-definable with parameters in
$\Sigma _1$
-definable with parameters in
![]() $V_\kappa $
proper class
$V_\kappa $
proper class
![]() ${\mathcal C}$
of structures in a fixed relational language
${\mathcal C}$
of structures in a fixed relational language
![]() $\tau \in V_\kappa $
, the set
$\tau \in V_\kappa $
, the set
![]() $S:={\mathcal C}\cap V_\kappa $
witnesses
$S:={\mathcal C}\cap V_\kappa $
witnesses
![]() $\Sigma _1(V_\kappa )$
-
$\Sigma _1(V_\kappa )$
-
![]() $\mathrm {PRP}$
.
$\mathrm {PRP}$
.
Proof Let
![]() $\kappa \in C^{(1)}$
, and let
$\kappa \in C^{(1)}$
, and let
![]() ${\mathcal C}$
be a
${\mathcal C}$
be a
![]() $\Sigma _1$
-definable, with a set of parameters
$\Sigma _1$
-definable, with a set of parameters
![]() $P\in V_\kappa $
, proper class of structures in a relational language
$P\in V_\kappa $
, proper class of structures in a relational language
![]() $\tau \in V_\kappa $
. Note that since
$\tau \in V_\kappa $
. Note that since
![]() $\kappa \in C^{(1)}$
,
$\kappa \in C^{(1)}$
,
![]() $V_\kappa =H_\kappa $
, and hence
$V_\kappa =H_\kappa $
, and hence
![]() $|\mathrm {TC}(\{ \tau \}\cup P)|<\kappa $
. Let
$|\mathrm {TC}(\{ \tau \}\cup P)|<\kappa $
. Let
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Sigma _1$
formula, with parameters in P, defining
$\Sigma _1$
formula, with parameters in P, defining
![]() ${\mathcal C}$
. We claim that
${\mathcal C}$
. We claim that
![]() $S:={\mathcal C}\cap V_\kappa $
satisfies
$S:={\mathcal C}\cap V_\kappa $
satisfies
![]() $\mathrm {PRP}$
. Given
$\mathrm {PRP}$
. Given
![]() $\mathcal {A}\in {\mathcal C}$
, let
$\mathcal {A}\in {\mathcal C}$
, let
![]() $\lambda \in C^{(1)}$
be greater than
$\lambda \in C^{(1)}$
be greater than
![]() $\kappa $
and such that
$\kappa $
and such that
![]() $\mathcal {A}\in V_\lambda $
. Let
$\mathcal {A}\in V_\lambda $
. Let
![]() $N\preceq V_\lambda $
be of cardinality less than
$N\preceq V_\lambda $
be of cardinality less than
![]() $\kappa $
and such that
$\kappa $
and such that
![]() $\mathcal {A}\in N$
and
$\mathcal {A}\in N$
and
![]() $\mathrm {TC}(\{ \tau \}\cup P)\subseteq N$
. Let
$\mathrm {TC}(\{ \tau \}\cup P)\subseteq N$
. Let
![]() $\pi :M\to N$
be the inverse transitive collapse isomorphism, and let
$\pi :M\to N$
be the inverse transitive collapse isomorphism, and let
![]() $\mathcal {B}\in M$
be such that
$\mathcal {B}\in M$
be such that
![]() $\pi (\mathcal {B})=\mathcal {A}$
. Notice that
$\pi (\mathcal {B})=\mathcal {A}$
. Notice that
![]() $\pi $
fixes
$\pi $
fixes
![]() $\tau $
and the parameters of
$\tau $
and the parameters of
![]() $\varphi (x)$
. Since M is transitive and of cardinality less than
$\varphi (x)$
. Since M is transitive and of cardinality less than
![]() $\kappa $
,
$\kappa $
,
![]() $\mathcal {B}\in H_\kappa =V_\kappa $
. Also, since
$\mathcal {B}\in H_\kappa =V_\kappa $
. Also, since
![]() $V_\lambda \models \varphi (\mathcal {A})$
, we have
$V_\lambda \models \varphi (\mathcal {A})$
, we have
![]() $N\models \varphi (\mathcal {A})$
, and therefore
$N\models \varphi (\mathcal {A})$
, and therefore
![]() $M\models \varphi (\mathcal {B})$
. Hence, since M is transitive and
$M\models \varphi (\mathcal {B})$
. Hence, since M is transitive and
![]() $\varphi $
is upwards absolute for transitive sets,
$\varphi $
is upwards absolute for transitive sets,
![]() $\mathcal {B}\in {\mathcal C}$
. Thus,
$\mathcal {B}\in {\mathcal C}$
. Thus,
![]() $\mathcal {B}\in S$
. Then the composition of
$\mathcal {B}\in S$
. Then the composition of
![]() $\pi $
with the projection
$\pi $
with the projection
![]() $\prod S\to \mathcal {B}$
yields the desired homomorphism.
$\prod S\to \mathcal {B}$
yields the desired homomorphism.
Proposition 3.3. If
![]() $\kappa $
is a strong cardinal, then
$\kappa $
is a strong cardinal, then
![]() $\Sigma _2(V_\kappa )$
-
$\Sigma _2(V_\kappa )$
-
![]() $\mathrm {PRP}$
holds.
$\mathrm {PRP}$
holds.
Proof Let
![]() $\kappa $
be a strong cardinal and let
$\kappa $
be a strong cardinal and let
![]() ${\mathcal C}$
be a
${\mathcal C}$
be a
![]() $\Sigma _2$
-definable, with parameters in
$\Sigma _2$
-definable, with parameters in
![]() $V_\kappa $
, proper class of structures in a fixed relational language
$V_\kappa $
, proper class of structures in a fixed relational language
![]() $\tau \in V_\kappa $
. Let
$\tau \in V_\kappa $
. Let
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Sigma _2$
formula defining it. We will show that
$\Sigma _2$
formula defining it. We will show that
![]() $S:={\mathcal C} \cap V_\kappa $
witnesses
$S:={\mathcal C} \cap V_\kappa $
witnesses
![]() $\mathrm {PRP}$
.
$\mathrm {PRP}$
.
Given any
![]() $\mathcal {A}\in {\mathcal C}$
, let
$\mathcal {A}\in {\mathcal C}$
, let
![]() $\lambda \in C^{(2)}$
be greater than or equal to
$\lambda \in C^{(2)}$
be greater than or equal to
![]() $\kappa $
and with
$\kappa $
and with
![]() $\mathcal {A}\in V_\lambda $
.
$\mathcal {A}\in V_\lambda $
.
Let
![]() $j:V\to M$
be an elementary embedding with
$j:V\to M$
be an elementary embedding with
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $j(\kappa )>\lambda $
.
$j(\kappa )>\lambda $
.
By elementarity, the restriction of j to
![]() $\prod S$
yields a homomorphism
$\prod S$
yields a homomorphism
Since
![]() $\mathcal {A}\in V_\lambda $
, and
$\mathcal {A}\in V_\lambda $
, and
![]() $\lambda \in C^{(2)}$
, we have that
$\lambda \in C^{(2)}$
, we have that
![]() $V_\lambda \models \varphi (\mathcal {A})$
. Since
$V_\lambda \models \varphi (\mathcal {A})$
. Since
![]() $\lambda \in C^{(1)}$
is
$\lambda \in C^{(1)}$
is
![]() $\Pi _1$
-expressible and therefore downwards absolute for transitive classes, and since
$\Pi _1$
-expressible and therefore downwards absolute for transitive classes, and since
![]() ${V_\lambda \subseteq M}$
, it follows that
${V_\lambda \subseteq M}$
, it follows that
![]() $V_\lambda \preceq _{\Sigma _1}M$
and therefore
$V_\lambda \preceq _{\Sigma _1}M$
and therefore
![]() $M\models \varphi (\mathcal {A})$
. Moreover
$M\models \varphi (\mathcal {A})$
. Moreover
![]() $\mathcal {A}\in V_\lambda \subseteq V^M_{j(\kappa )}$
. Thus, letting
$\mathcal {A}\in V_\lambda \subseteq V^M_{j(\kappa )}$
. Thus, letting
be the projection map, we have that
is a homomorphism, as wanted.
Corollary 3.4. If there exists a proper class of strong cardinals, then
![]() ${\mathbf \Sigma _2}$
-
${\mathbf \Sigma _2}$
-
![]() $\mathrm {PRP}$
holds.
$\mathrm {PRP}$
holds.
We shall next show that
![]() $\mathrm {SWVP}$
is equivalent to the assertion that
$\mathrm {SWVP}$
is equivalent to the assertion that
![]() $\mathrm {PRP}$
holds for all definable proper classes of structures. Let
$\mathrm {PRP}$
holds for all definable proper classes of structures. Let
![]() $\Gamma _n$
be either
$\Gamma _n$
be either
![]() $\Sigma _n$
or
$\Sigma _n$
or
![]() $\Pi _n$
.
$\Pi _n$
.
Proposition 3.5.
![]() $\Gamma _n (P)$
-
$\Gamma _n (P)$
-
![]() $\mathrm {PRP}$
implies
$\mathrm {PRP}$
implies
![]() $\Gamma _{n}(P)$
-
$\Gamma _{n}(P)$
-
![]() $\mathrm {SWVP}$
, for every
$\mathrm {SWVP}$
, for every
![]() $n>0$
and every class P.
$n>0$
and every class P.
Proof Assume
![]() $\mathcal {G} = \langle G_\alpha : \alpha \in \text {OR}\rangle $
is a sequence of graphs that is definable by a
$\mathcal {G} = \langle G_\alpha : \alpha \in \text {OR}\rangle $
is a sequence of graphs that is definable by a
![]() $\Gamma _n$
formula
$\Gamma _n$
formula
![]() $\varphi $
from a parameter
$\varphi $
from a parameter
![]() $p \in P$
, such that whenever
$p \in P$
, such that whenever
![]() $\alpha \le \beta $
there is a homomorphism
$\alpha \le \beta $
there is a homomorphism
![]() $G_\beta \to G_\alpha $
. We shall use
$G_\beta \to G_\alpha $
. We shall use
![]() $\Gamma _n(P)$
-PRP to produce a homomorphism
$\Gamma _n(P)$
-PRP to produce a homomorphism
![]() $G_\beta \to G_{\gamma }$
for some
$G_\beta \to G_{\gamma }$
for some
![]() $\gamma> \beta $
, thereby witnessing the desired instance of SWVP.
$\gamma> \beta $
, thereby witnessing the desired instance of SWVP.
In the case
![]() $\Gamma _n = \Sigma _n$
we define the class of graphs
$\Gamma _n = \Sigma _n$
we define the class of graphs
![]() $\mathcal {C} = \{G_\alpha : \alpha \in \text {OR}\}$
, which is
$\mathcal {C} = \{G_\alpha : \alpha \in \text {OR}\}$
, which is
![]() $\Sigma _n$
-definable from the parameter
$\Sigma _n$
-definable from the parameter
![]() $p \in P$
because a graph G is in
$p \in P$
because a graph G is in
![]() $\mathcal {C}$
if and only if
$\mathcal {C}$
if and only if
![]() $\exists \alpha \in \text {OR}\;\varphi (\alpha , G, p)$
and the formula
$\exists \alpha \in \text {OR}\;\varphi (\alpha , G, p)$
and the formula
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma _n$
. Therefore by
$\Sigma _n$
. Therefore by
![]() $\Sigma _n(P)$
-PRP, there is a subset
$\Sigma _n(P)$
-PRP, there is a subset
![]() $\mathcal {S}$
of the class
$\mathcal {S}$
of the class
![]() $\mathcal {C}$
such that for every
$\mathcal {C}$
such that for every
![]() $G \in \mathcal {C}$
there is a homomorphism
$G \in \mathcal {C}$
there is a homomorphism
![]() $\prod \mathcal {S} \to G$
. This gives a subset I of the class
$\prod \mathcal {S} \to G$
. This gives a subset I of the class
![]() $\text {OR}$
such that for every
$\text {OR}$
such that for every
![]() $\gamma \in \text {OR}$
there is a homomorphism
$\gamma \in \text {OR}$
there is a homomorphism
![]() $\prod _{\alpha \in I} G_\alpha \to G_\gamma $
. In particular, letting
$\prod _{\alpha \in I} G_\alpha \to G_\gamma $
. In particular, letting
![]() $\beta = \sup I$
and
$\beta = \sup I$
and
![]() $\gamma> \beta $
(for example,
$\gamma> \beta $
(for example,
![]() $\gamma = \beta + 1$
), there is a homomorphism
$\gamma = \beta + 1$
), there is a homomorphism
![]() $\prod _{\alpha \in I} G_\alpha \to G_{\gamma }$
. Composing this with a homomorphism
$\prod _{\alpha \in I} G_\alpha \to G_{\gamma }$
. Composing this with a homomorphism
![]() $G_\beta \to \prod _{\alpha \in I} G_\alpha $
(which exists because for each
$G_\beta \to \prod _{\alpha \in I} G_\alpha $
(which exists because for each
![]() $\alpha \in I$
there is a homomorphism
$\alpha \in I$
there is a homomorphism
![]() $G_\beta \to G_\alpha $
) we obtain a homomorphism
$G_\beta \to G_\alpha $
) we obtain a homomorphism
![]() $G_\beta \to G_{\gamma }$
, as desired.
$G_\beta \to G_{\gamma }$
, as desired.
In the case
![]() $\Gamma _n = \Pi _n$
, we will need the following preliminary observation. Namely, we may assume without loss of generality that for every
$\Gamma _n = \Pi _n$
, we will need the following preliminary observation. Namely, we may assume without loss of generality that for every
![]() $\kappa $
the class
$\kappa $
the class
![]() $\{\alpha \in \text {OR} : |G_\alpha | \le \kappa \}$
is bounded by some ordinal
$\{\alpha \in \text {OR} : |G_\alpha | \le \kappa \}$
is bounded by some ordinal
![]() $f(\kappa )$
, as otherwise it would contain two distinct
$f(\kappa )$
, as otherwise it would contain two distinct
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
such that
$\alpha '$
such that
![]() $G_\alpha $
and
$G_\alpha $
and
![]() $G_{\alpha '}$
are isomorphic, trivially witnessing the desired instance of SWVP. It follows that the class
$G_{\alpha '}$
are isomorphic, trivially witnessing the desired instance of SWVP. It follows that the class
![]() $\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
contains a club class (namely the class of all closure points of this bounding function f) and in particular it is a proper class. We therefore define the class of graphs
$\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
contains a club class (namely the class of all closure points of this bounding function f) and in particular it is a proper class. We therefore define the class of graphs
which is
![]() $\Pi _n$
-definable from the parameter
$\Pi _n$
-definable from the parameter
![]() $p \in P$
because a graph G is in
$p \in P$
because a graph G is in
![]() $\mathcal {C}$
if and only if
$\mathcal {C}$
if and only if
and the formula
![]() $\varphi $
is
$\varphi $
is
![]() $\Pi _n$
. (The main point is that the existential quantification over
$\Pi _n$
. (The main point is that the existential quantification over
![]() $\alpha $
is bounded.) Therefore, by
$\alpha $
is bounded.) Therefore, by
![]() $\Pi _n(P)$
-PRP, there is a subset
$\Pi _n(P)$
-PRP, there is a subset
![]() $\mathcal {S}$
of the class
$\mathcal {S}$
of the class
![]() $\mathcal {C}$
such that for every graph
$\mathcal {C}$
such that for every graph
![]() $G \in \mathcal {C}$
there is a homomorphism
$G \in \mathcal {C}$
there is a homomorphism
![]() $\prod \mathcal {S} \to G$
. This gives a subset I of the class
$\prod \mathcal {S} \to G$
. This gives a subset I of the class
![]() $\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
such that for every ordinal
$\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
such that for every ordinal
![]() $\gamma $
in that class, there is a homomorphism
$\gamma $
in that class, there is a homomorphism
![]() $\prod _{\alpha \in I} G_\alpha \to G_\gamma $
. Letting
$\prod _{\alpha \in I} G_\alpha \to G_\gamma $
. Letting
![]() $\beta = \sup I$
, because the class
$\beta = \sup I$
, because the class
![]() $\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
is a proper class, it contains some ordinal
$\{\alpha \in \text {OR} : |G_\alpha | \ge \alpha \}$
is a proper class, it contains some ordinal
![]() $\gamma> \beta $
. We may then proceed as in the
$\gamma> \beta $
. We may then proceed as in the
![]() $\Sigma _n$
case to obtain a homomorphism
$\Sigma _n$
case to obtain a homomorphism
![]() $G_\beta \to G_{\gamma }$
, as desired.
$G_\beta \to G_{\gamma }$
, as desired.
The converse also holds, and in fact more is true. Namely,
Proposition 3.6.
![]() $\Pi _{n}(P)$
-
$\Pi _{n}(P)$
-
![]() $\mathrm {WVP}$
implies
$\mathrm {WVP}$
implies
![]() $\Sigma _{n+1} (P)$
-
$\Sigma _{n+1} (P)$
-
![]() $\mathrm {PRP}$
, for every
$\mathrm {PRP}$
, for every
![]() $n\in \omega $
, and every P.
$n\in \omega $
, and every P.
Proof Let
![]() $\mathcal {C}$
be a
$\mathcal {C}$
be a
![]() $\Sigma _{n+1}$
-definable, with parameter
$\Sigma _{n+1}$
-definable, with parameter
![]() $p\in P$
, class of graphs that is a counterexample to PRP. We may represent this class as an increasing union:
$p\in P$
, class of graphs that is a counterexample to PRP. We may represent this class as an increasing union:
![]() $\mathcal {C} = \bigcup _{\beta \in C^{(n)}} \mathcal {C}^{V_{\beta }}$
where
$\mathcal {C} = \bigcup _{\beta \in C^{(n)}} \mathcal {C}^{V_{\beta }}$
where
![]() $\mathcal {C}^{V_{\beta }}$
is the relativization of
$\mathcal {C}^{V_{\beta }}$
is the relativization of
![]() $\mathcal {C}$
to
$\mathcal {C}$
to
![]() $V_\beta $
. Note that
$V_\beta $
. Note that
![]() $\mathcal {C}^{V_{\beta }}$
is a subset of
$\mathcal {C}^{V_{\beta }}$
is a subset of
![]() $\mathcal {C} \cap V_\beta $
for any
$\mathcal {C} \cap V_\beta $
for any
![]() $\beta \in C^{(n)}$
, and (unless
$\beta \in C^{(n)}$
, and (unless
![]() $\mathcal {C}$
happens to be
$\mathcal {C}$
happens to be
![]() $\Pi _n$
) it may be a proper subset, since the least witness to a
$\Pi _n$
) it may be a proper subset, since the least witness to a
![]() $\Sigma _{n+1}$
property of a graph may have much larger rank than the graph itself.
$\Sigma _{n+1}$
property of a graph may have much larger rank than the graph itself.
We recursively define a function
![]() $f : \text {Ord} \to \text {Ord}$
by letting
$f : \text {Ord} \to \text {Ord}$
by letting
![]() $f(0)$
be the least
$f(0)$
be the least
![]() $\beta \in C^{(n)}$
such that
$\beta \in C^{(n)}$
such that
![]() $\mathcal {C}^{V_\beta } \not = \varnothing $
, letting
$\mathcal {C}^{V_\beta } \not = \varnothing $
, letting
![]() $f(\alpha +1)$
be the least
$f(\alpha +1)$
be the least
![]() $\beta \in C^{(n)}$
such that there is no homomorphism
$\beta \in C^{(n)}$
such that there is no homomorphism
![]() $\prod \mathcal {C}^{V_{f(\alpha )}} \to \prod \mathcal {C}^{V_{\beta }}$
, and letting
$\prod \mathcal {C}^{V_{f(\alpha )}} \to \prod \mathcal {C}^{V_{\beta }}$
, and letting
![]() $f(\lambda ) = \sup _{\alpha < \lambda } f(\alpha )$
if
$f(\lambda ) = \sup _{\alpha < \lambda } f(\alpha )$
if
![]() $\lambda $
is a limit ordinal. To see that f is a total function, note that the ordinal
$\lambda $
is a limit ordinal. To see that f is a total function, note that the ordinal
![]() $\beta $
in the definition of
$\beta $
in the definition of
![]() $f(\alpha +1)$
exists: otherwise for any graph
$f(\alpha +1)$
exists: otherwise for any graph
![]() $G \in \mathcal {C}$
we could take
$G \in \mathcal {C}$
we could take
![]() $\beta \in C^{(n)}$
sufficiently large that
$\beta \in C^{(n)}$
sufficiently large that
![]() $G \in \mathcal {C}^{V_{\beta }}$
and then compose a homomorphism
$G \in \mathcal {C}^{V_{\beta }}$
and then compose a homomorphism
![]() $\prod \mathcal {C}^{V_{f(\alpha )}} \to \prod \mathcal {C}^{V_{\beta }}$
with a projection homomorphism to obtain a homomorphism
$\prod \mathcal {C}^{V_{f(\alpha )}} \to \prod \mathcal {C}^{V_{\beta }}$
with a projection homomorphism to obtain a homomorphism
![]() $\prod \mathcal {C}^{V_{f(\alpha )}} \to G$
, thereby witnessing PRP for
$\prod \mathcal {C}^{V_{f(\alpha )}} \to G$
, thereby witnessing PRP for
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
For every ordinal
![]() $\alpha $
we define the product graph
$\alpha $
we define the product graph
Note that the sequence
![]() $\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
is a counterexample to SWVP (which we do not claim to be
$\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
is a counterexample to SWVP (which we do not claim to be
![]() $\Pi _n$
or even
$\Pi _n$
or even
![]() $\Sigma _{n+1}$
): for every pair of ordinals
$\Sigma _{n+1}$
): for every pair of ordinals
![]() $\alpha \le \alpha '$
there is a homomorphism from
$\alpha \le \alpha '$
there is a homomorphism from
![]() $H_{\alpha '}$
to
$H_{\alpha '}$
to
![]() $H_{\alpha }$
given by restriction, and for every ordinal
$H_{\alpha }$
given by restriction, and for every ordinal
![]() $\alpha $
the definition of f implies there is no homomorphism from
$\alpha $
the definition of f implies there is no homomorphism from
![]() $H_{\alpha }$
to
$H_{\alpha }$
to
![]() $H_{\alpha +1}$
(nor to
$H_{\alpha +1}$
(nor to
![]() $H_{\alpha '}$
for any larger
$H_{\alpha '}$
for any larger
![]() $\alpha '$
, or else we could compose with a restriction homomorphism to get a homomorphism to
$\alpha '$
, or else we could compose with a restriction homomorphism to get a homomorphism to
![]() $H_{\alpha +1}$
.) We will use this sequence to build a counterexample to WVP, which moreover will be
$H_{\alpha +1}$
.) We will use this sequence to build a counterexample to WVP, which moreover will be
![]() $\Pi _n$
.
$\Pi _n$
.
Let
![]() $\Lambda $
be the class of all limit ordinals that are fixed points of f. Equivalently because f is continuous and increasing,
$\Lambda $
be the class of all limit ordinals that are fixed points of f. Equivalently because f is continuous and increasing,
![]() $\Lambda $
is the class of all limit ordinals that are closed under f. Note that
$\Lambda $
is the class of all limit ordinals that are closed under f. Note that
![]() $\Lambda $
is a closed unbounded class and
$\Lambda $
is a closed unbounded class and
![]() $\Lambda \subseteq C^{(n)}$
(so in particular the elements of
$\Lambda \subseteq C^{(n)}$
(so in particular the elements of
![]() $\lambda $
are limit cardinals, although we won’t use this fact directly.) For every pair of ordinals
$\lambda $
are limit cardinals, although we won’t use this fact directly.) For every pair of ordinals
![]() $\lambda \le \lambda '$
in
$\lambda \le \lambda '$
in
![]() $\Lambda $
we define the function
$\Lambda $
we define the function
![]() $h_{\lambda '\lambda } : V_{\lambda '+1} \to V_{\lambda +1}$
by
$h_{\lambda '\lambda } : V_{\lambda '+1} \to V_{\lambda +1}$
by
We will define some structure (constants and relations) on the sets
![]() $V_{\lambda +1}$
(
$V_{\lambda +1}$
(
![]() ${\lambda \in \Lambda }$
) that is preserved by these functions
${\lambda \in \Lambda }$
) that is preserved by these functions
![]() $h_{\lambda '\lambda }$
and not by any other functions. To ensure that the structure is not preserved by any other functions, it will encode our counterexample
$h_{\lambda '\lambda }$
and not by any other functions. To ensure that the structure is not preserved by any other functions, it will encode our counterexample
![]() $\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
to SWVP (among other things.) The coding will use a “stratified” version
$\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
to SWVP (among other things.) The coding will use a “stratified” version
![]() $H_\alpha ^*$
of the product graph
$H_\alpha ^*$
of the product graph
![]() $H_\alpha $
, which we define as a double product of length
$H_\alpha $
, which we define as a double product of length
![]() $1+\alpha $
, having
$1+\alpha $
, having
![]() $\prod \mathcal {C}^{V_{f(0)}}$
as initial factor, namely:
$\prod \mathcal {C}^{V_{f(0)}}$
as initial factor, namely:
Note that the graph
![]() $H_\alpha ^*$
is isomorphic to
$H_\alpha ^*$
is isomorphic to
![]() $H_\alpha $
(the initial factor was added to ensure this in the case
$H_\alpha $
(the initial factor was added to ensure this in the case
![]() $\alpha =0$
), and it has the advantage that for every pair of ordinals
$\alpha =0$
), and it has the advantage that for every pair of ordinals
![]() $\lambda \le \lambda '$
in
$\lambda \le \lambda '$
in
![]() $\Lambda $
, the function
$\Lambda $
, the function
![]() $h_{\lambda '\lambda }$
is a homomorphism from
$h_{\lambda '\lambda }$
is a homomorphism from
![]() $H^*_{\lambda '}$
to
$H^*_{\lambda '}$
to
![]() $H^*_{\lambda }$
because it just restricts the outermost product from
$H^*_{\lambda }$
because it just restricts the outermost product from
![]() $\prod _{\alpha _0 < \lambda '}$
to
$\prod _{\alpha _0 < \lambda '}$
to
![]() $\prod _{\alpha _0 < \lambda }$
, whereas it might not be a homomorphism from
$\prod _{\alpha _0 < \lambda }$
, whereas it might not be a homomorphism from
![]() $H_{\lambda '}$
to
$H_{\lambda '}$
to
![]() $H_{\lambda }$
because
$H_{\lambda }$
because
![]() $\mathcal {C}^{V_{\lambda '}} \cap V_{\lambda }$
might not be equal to
$\mathcal {C}^{V_{\lambda '}} \cap V_{\lambda }$
might not be equal to
![]() $\mathcal {C}^{V_\lambda }$
.
$\mathcal {C}^{V_\lambda }$
.
Our structures will be defined as in [Reference Wilson12] except using the graph
![]() $H_\alpha ^*$
in place of
$H_\alpha ^*$
in place of
![]() $H_\alpha $
. Namely, we let
$H_\alpha $
. Namely, we let
![]() $\Sigma $
be the signature with a constant symbol c and ternary relation symbols R, S, and T, and for every ordinal
$\Sigma $
be the signature with a constant symbol c and ternary relation symbols R, S, and T, and for every ordinal
![]() $\lambda \in \Lambda $
we define a corresponding
$\lambda \in \Lambda $
we define a corresponding
![]() $\Sigma $
-structure
$\Sigma $
-structure
where
![]() $c^{\mathcal {M}_\lambda } = \lambda $
and the interpretations of R, S, and T are defined as follows:
$c^{\mathcal {M}_\lambda } = \lambda $
and the interpretations of R, S, and T are defined as follows:
 $$ \begin{align*} R^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff \big(\alpha = \mathrm{rank}(x) \text{ and } x \in y\big) \text{ or } \alpha = \lambda,\\ S^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff \big(\alpha = \mathrm{rank}(x) \text{ and } x \notin y\big) \text{ or } \alpha = \lambda,\\ T^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff x\ \text{is adjacent to}\ y\ \text{in}\ H_\alpha^*. \end{align*} $$
$$ \begin{align*} R^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff \big(\alpha = \mathrm{rank}(x) \text{ and } x \in y\big) \text{ or } \alpha = \lambda,\\ S^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff \big(\alpha = \mathrm{rank}(x) \text{ and } x \notin y\big) \text{ or } \alpha = \lambda,\\ T^{\mathcal{M}_\lambda}(\alpha, x,y) &\iff x\ \text{is adjacent to}\ y\ \text{in}\ H_\alpha^*. \end{align*} $$
(In the definition of
![]() $T^{\mathcal {M}_\lambda }$
we take x and y to be vertices of
$T^{\mathcal {M}_\lambda }$
we take x and y to be vertices of
![]() $H_\alpha ^*$
.)
$H_\alpha ^*$
.)
Essentially the same argument as in [Reference Wilson12] shows that the only homomorphisms among the structures
![]() $\mathcal {M}_\lambda $
for
$\mathcal {M}_\lambda $
for
![]() $\lambda \in \Lambda $
are the homomorphisms
$\lambda \in \Lambda $
are the homomorphisms
![]() $h_{\lambda '\lambda }$
for
$h_{\lambda '\lambda }$
for
![]() $\lambda \le \lambda '$
. Here we will just remind the reader of the main idea of that argument, which is that for any ordinals
$\lambda \le \lambda '$
. Here we will just remind the reader of the main idea of that argument, which is that for any ordinals
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda '$
in
$\lambda '$
in
![]() $\Lambda $
:
$\Lambda $
:
-
(1) If
 $\lambda < \lambda '$
, then preservation of the T relation and the constant c ensures that any “forward” homomorphism from
$\lambda < \lambda '$
, then preservation of the T relation and the constant c ensures that any “forward” homomorphism from
 $\mathcal {M}_\lambda $
to
$\mathcal {M}_\lambda $
to
 $\mathcal {M}_{\lambda '}$
would produce a homomorphism from
$\mathcal {M}_{\lambda '}$
would produce a homomorphism from
 $H^*_{\lambda }$
to
$H^*_{\lambda }$
to
 $H^*_{\lambda '}$
, or equivalently from
$H^*_{\lambda '}$
, or equivalently from
 $H_{\lambda }$
to
$H_{\lambda }$
to
 $H_{\lambda '}$
, contradicting the fact that
$H_{\lambda '}$
, contradicting the fact that
 $\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
is a counterexample to SWVP.
$\langle H_\alpha : \alpha \in \mathrm {Ord}\rangle $
is a counterexample to SWVP. -
(2) If
 $\lambda \le \lambda '$
, then preservation of the R and S relations (which encode the membership relation
$\lambda \le \lambda '$
, then preservation of the R and S relations (which encode the membership relation
 $\in $
) ensures that any “reverse” homomorphism from
$\in $
) ensures that any “reverse” homomorphism from
 $\mathcal {M}_{\lambda '}$
to
$\mathcal {M}_{\lambda '}$
to
 $\mathcal {M}_{\lambda }$
that is not equal to
$\mathcal {M}_{\lambda }$
that is not equal to
 $h_{\lambda '\lambda }$
would have a critical point that is mapped forward, which would then yield a contradiction using preservation of the T relation by an argument similar to (1).
$h_{\lambda '\lambda }$
would have a critical point that is mapped forward, which would then yield a contradiction using preservation of the T relation by an argument similar to (1).
Enumerating
![]() $\Lambda $
in increasing order as
$\Lambda $
in increasing order as
![]() $\langle \lambda _\xi : \xi \in \mathrm {Ord}\rangle $
, or in other words letting
$\langle \lambda _\xi : \xi \in \mathrm {Ord}\rangle $
, or in other words letting
![]() $\lambda _\xi $
be the
$\lambda _\xi $
be the
![]() $\xi $
th fixed point of f, the sequence of structures
$\xi $
th fixed point of f, the sequence of structures
is therefore a counterexample to WVP. It remains to check that this sequence of structures is
![]() $\Pi _n$
. For any ordinal
$\Pi _n$
. For any ordinal
![]() $\xi $
and any structure
$\xi $
and any structure
![]() $\mathcal {M}$
, the condition
$\mathcal {M}$
, the condition
![]() $\mathcal {M} = \mathcal {M}_{\lambda _\xi }$
is equivalent to the conjunction of the following conditions, each of which can be expressed by a
$\mathcal {M} = \mathcal {M}_{\lambda _\xi }$
is equivalent to the conjunction of the following conditions, each of which can be expressed by a
![]() $\Pi _n$
formula (or simpler):
$\Pi _n$
formula (or simpler):
-
(1)
 $\mathcal {M}$
is a
$\mathcal {M}$
is a
 $\Sigma $
-structure whose underlying set M contains a largest ordinal
$\Sigma $
-structure whose underlying set M contains a largest ordinal
 $\lambda $
. This condition can be expressed by a bounded formula.
$\lambda $
. This condition can be expressed by a bounded formula. -
(2) M is a rank initial segment of V (which must therefore be equal to
 $V_{\lambda + 1}$
.) This condition is
$V_{\lambda + 1}$
.) This condition is
 $\Pi _1$
.
$\Pi _1$
. -
(3)
 $\lambda $
is in the class
$\lambda $
is in the class
 $C^{(n)}$
. This condition is
$C^{(n)}$
. This condition is
 $\Pi _n$
.
$\Pi _n$
. -
(4)
 $\lambda $
is equal to
$\lambda $
is equal to
 $\lambda _\xi $
, the
$\lambda _\xi $
, the
 $\xi $
th closure point of f. Given that
$\xi $
th closure point of f. Given that
 $M = V_{\lambda +1}$
where
$M = V_{\lambda +1}$
where
 $\lambda \in C^{(n)}$
, this condition can be expressed by a bounded formula over M. To see this, first note that the definition of the class
$\lambda \in C^{(n)}$
, this condition can be expressed by a bounded formula over M. To see this, first note that the definition of the class
 $C^{(n)}$
is
$C^{(n)}$
is
 $\Pi _n$
and therefore absolute to
$\Pi _n$
and therefore absolute to
 $V_\lambda $
. Second, note that the definition of f (as a relation and in particular as a partial function) using
$V_\lambda $
. Second, note that the definition of f (as a relation and in particular as a partial function) using
 $C^{(n)}$
is also absolute to
$C^{(n)}$
is also absolute to
 $V_\lambda $
. For the absoluteness of f, note that the complexity of
$V_\lambda $
. For the absoluteness of f, note that the complexity of
 $\mathcal {C}$
doesn’t make f complex, because f is defined using relativizations of
$\mathcal {C}$
doesn’t make f complex, because f is defined using relativizations of
 $\mathcal {C}$
that can be computed locally; also note that the construction of product graphs is absolute to
$\mathcal {C}$
that can be computed locally; also note that the construction of product graphs is absolute to
 $V_\lambda $
, as is the existence of a homomorphism between any two given graphs.
$V_\lambda $
, as is the existence of a homomorphism between any two given graphs.Third, note that because f is absolute to
 $V_\lambda $
, it follows that
$V_\lambda $
, it follows that
 $V_\lambda $
can see whether or not
$V_\lambda $
can see whether or not
 $\lambda $
is a closure point of f. (This holds if and only if the relativization of f to
$\lambda $
is a closure point of f. (This holds if and only if the relativization of f to
 $V_\lambda $
is a total function on
$V_\lambda $
is a total function on
 $\lambda $
.) Finally, note that M can see more specifically whether or not
$\lambda $
.) Finally, note that M can see more specifically whether or not
 $\lambda $
is the
$\lambda $
is the
 $\xi $
th closure point of f: in the case that
$\xi $
th closure point of f: in the case that
 $\xi \in M$
, this again follows from the absoluteness of f to
$\xi \in M$
, this again follows from the absoluteness of f to
 $V_\lambda $
, but actually the case that
$V_\lambda $
, but actually the case that
 $\xi \in M$
is the only case we need to consider, because
$\xi \in M$
is the only case we need to consider, because
 $M = V_{\lambda +1}$
and for
$M = V_{\lambda +1}$
and for
 $\lambda $
to be the
$\lambda $
to be the
 $\xi $
th closure point of f would require
$\xi $
th closure point of f would require
 $\xi \le \lambda $
and therefore
$\xi \le \lambda $
and therefore
 $\xi \in M$
.
$\xi \in M$
. -
(5) The constant and the three relations of the
 $\Sigma $
-structure
$\Sigma $
-structure
 $\mathcal {M}$
are defined correctly, meaning
$\mathcal {M}$
are defined correctly, meaning
 $c^{\mathcal {M}} = c^{\mathcal {M}_\lambda }$
,
$c^{\mathcal {M}} = c^{\mathcal {M}_\lambda }$
,
 $R^{\mathcal {M}}= R^{\mathcal {M}_\lambda }$
,
$R^{\mathcal {M}}= R^{\mathcal {M}_\lambda }$
,
 $S^{\mathcal {M}} =S^{\mathcal {M}_\lambda }$
, and
$S^{\mathcal {M}} =S^{\mathcal {M}_\lambda }$
, and
 $T^{\mathcal {M}} =T^{\mathcal {M}_\lambda }$
, defined as above. Given that the underlying set M of this structure is equal to
$T^{\mathcal {M}} =T^{\mathcal {M}_\lambda }$
, defined as above. Given that the underlying set M of this structure is equal to
 $V_{\lambda +1}$
where
$V_{\lambda +1}$
where
 $\lambda $
is a closure point of f (and is therefore in
$\lambda $
is a closure point of f (and is therefore in
 $C^{(n)}$
) these four conditions can be expressed by bounded formulas over the structure
$C^{(n)}$
) these four conditions can be expressed by bounded formulas over the structure
 $\mathcal {M}$
. We show this only for the condition
$\mathcal {M}$
. We show this only for the condition
 $T^{\mathcal {M}} =T^{\mathcal {M}_\lambda }$
, since the other three are relatively straightforward.
$T^{\mathcal {M}} =T^{\mathcal {M}_\lambda }$
, since the other three are relatively straightforward.First, note that the definition of the sequence of graphs
 $\langle H^*_\alpha : \alpha < \lambda \rangle $
is absolute to
$\langle H^*_\alpha : \alpha < \lambda \rangle $
is absolute to
 $V_\lambda $
: again the complexity of the class
$V_\lambda $
: again the complexity of the class
 $\mathcal {C}$
doesn’t matter because f and
$\mathcal {C}$
doesn’t matter because f and
 $H^*_\alpha $
are defined using local relativizations of it. Second, note that the vertex set and edge relation of the graph
$H^*_\alpha $
are defined using local relativizations of it. Second, note that the vertex set and edge relation of the graph
 $H^*_\lambda $
are definable by bounded formulas over
$H^*_\lambda $
are definable by bounded formulas over
 $V_{\lambda +1}$
for a similar reason. These two observations show that the correct relation
$V_{\lambda +1}$
for a similar reason. These two observations show that the correct relation
 $T^{\mathcal {M}_\lambda }$
is definable by a bounded formula over the set
$T^{\mathcal {M}_\lambda }$
is definable by a bounded formula over the set
 $M = V_{\lambda +1}$
, so the structure
$M = V_{\lambda +1}$
, so the structure
 $\mathcal {M}$
can see whether or not
$\mathcal {M}$
can see whether or not
 $T^{\mathcal {M}_\lambda }$
agrees with its own relation
$T^{\mathcal {M}_\lambda }$
agrees with its own relation
 $T^{\mathcal {M}}$
.⊣
$T^{\mathcal {M}}$
.⊣
The following is now an immediate consequence of Propositions 3.5 and 3.6.
Theorem 3.7. For every
![]() $n>0$
and every set or proper class P, the following are equivalent:
$n>0$
and every set or proper class P, the following are equivalent:
-
(1)
 $\Sigma _{n+1}(P)$
-
$\Sigma _{n+1}(P)$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(2)
 $\Pi _n(P)$
-
$\Pi _n(P)$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(3)
 $\Sigma _{n+1}(P)$
-
$\Sigma _{n+1}(P)$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(4)
 $\Pi _n(P)$
-
$\Pi _n(P)$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(5)
 $\Sigma _{n+1}(P)$
-
$\Sigma _{n+1}(P)$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
. -
(6)
 $\Pi _n(P)$
-
$\Pi _n(P)$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
Proof The implications
![]() $(1)\Rightarrow (2)$
,
$(1)\Rightarrow (2)$
,
![]() $(3)\Rightarrow (4)$
, and
$(3)\Rightarrow (4)$
, and
![]() $(5)\Rightarrow (6)$
are trivial. The implications
$(5)\Rightarrow (6)$
are trivial. The implications
![]() $(3)\Rightarrow (5)$
and
$(3)\Rightarrow (5)$
and
![]() $(4)\Rightarrow (6)$
are clear. Proposition 3.5 yields
$(4)\Rightarrow (6)$
are clear. Proposition 3.5 yields
![]() $(1)\Rightarrow (3)$
and
$(1)\Rightarrow (3)$
and
![]() $(2)\Rightarrow (4)$
. Finally, Proposition 3.6 yields
$(2)\Rightarrow (4)$
. Finally, Proposition 3.6 yields
![]() $(6)\Rightarrow (1)$
.
$(6)\Rightarrow (1)$
.
In the next two sections we shall prove, for each
![]() $n>0$
, exact equivalences of (1)–(6) above with large cardinals.
$n>0$
, exact equivalences of (1)–(6) above with large cardinals.
4 The main theorem for strong cardinals
Theorem 4.1. The following are equivalent:
-
(1) There exists a strong cardinal.
-
(2)
 $\Sigma _2$
-
$\Sigma _2$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(3)
 $\Pi _1$
-
$\Pi _1$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(4)
 $\Sigma _2$
-
$\Sigma _2$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(5)
 $\Pi _1$
-
$\Pi _1$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(6)
 $\Sigma _2$
-
$\Sigma _2$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
. -
(7)
 $\Pi _1$
-
$\Pi _1$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
Proof (1)
![]() $\Rightarrow $
(2) is given by Proposition 3.3. The equivalence of (2)–(7) is given by Theorem 3.7. So, it will be sufficient to prove (3)
$\Rightarrow $
(2) is given by Proposition 3.3. The equivalence of (2)–(7) is given by Theorem 3.7. So, it will be sufficient to prove (3)
![]() $\Rightarrow $
(1).
$\Rightarrow $
(1).
(3)
![]() $\Rightarrow $
(1): Let
$\Rightarrow $
(1): Let
![]() $\mathcal {A}$
be the class of all structures
$\mathcal {A}$
be the class of all structures
where the constant
![]() $ \alpha $
is the
$ \alpha $
is the
![]() $\alpha $
-th element of
$\alpha $
-th element of
![]() $C^{(1)}$
and
$C^{(1)}$
and
![]() $\{ R^{\alpha }_\varphi \}_{\varphi \in \Pi _1}$
is the
$\{ R^{\alpha }_\varphi \}_{\varphi \in \Pi _1}$
is the
![]() $\Pi _1$
relational diagram for
$\Pi _1$
relational diagram for
![]() $V_{\alpha +1}$
, i.e., if
$V_{\alpha +1}$
, i.e., if
![]() $\varphi (x_1,\ldots ,x_n)$
is a
$\varphi (x_1,\ldots ,x_n)$
is a
![]() $\Pi _1$
formula in the language of
$\Pi _1$
formula in the language of
![]() $\langle V_{ \alpha +1},\in ,\alpha \rangle $
, then
$\langle V_{ \alpha +1},\in ,\alpha \rangle $
, then
We claim that
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\Pi _1$
-definable without parameters. For
$\Pi _1$
-definable without parameters. For
![]() $X\in \mathcal {A}$
if and only if
$X\in \mathcal {A}$
if and only if
![]() $X=\langle X_0,X_1,X_2,X_3 \rangle $
, where:
$X=\langle X_0,X_1,X_2,X_3 \rangle $
, where:
-
(1)
 $X_2$
belongs to
$X_2$
belongs to
 $C^{(1)}$
,
$C^{(1)}$
, -
(2)
 $X_0=V_{X_2 +1}$
,
$X_0=V_{X_2 +1}$
, -
(3)
 $X_1 = \mathord {\in } \restriction X_0$
,
$X_1 = \mathord {\in } \restriction X_0$
, -
(4)
 $X_3$
is the
$X_3$
is the
 $\Pi _1$
relational diagram of
$\Pi _1$
relational diagram of
 $\langle X_0,X_1,X_2 \rangle $
, and
$\langle X_0,X_1,X_2 \rangle $
, and -
(5)
 $\langle X_0, X_1, X_2 \rangle \models “X_2$
is the
$\langle X_0, X_1, X_2 \rangle \models “X_2$
is the
 $X_2$
-th element of
$X_2$
-th element of
 $C^{(1)}$
.”
$C^{(1)}$
.”
Note that
![]() $\mathcal {A}$
is a proper class. In fact, the class C of ordinals
$\mathcal {A}$
is a proper class. In fact, the class C of ordinals
![]() $\alpha $
such that
$\alpha $
such that
![]() ${\mathcal A}_\alpha \in {\mathcal A}$
is a closed and unbounded proper class. By
${\mathcal A}_\alpha \in {\mathcal A}$
is a closed and unbounded proper class. By
![]() $\Pi _1$
-
$\Pi _1$
-
![]() $\mathrm {PRP}$
there exists a subset S of C such that for every
$\mathrm {PRP}$
there exists a subset S of C such that for every
![]() $\beta \in C$
there is a homomorphism
$\beta \in C$
there is a homomorphism
![]() $j_\beta : \prod _{\alpha \in S} {\mathcal A}_\alpha \to {\mathcal A}_\beta $
. By enlarging S, if necessary, we may assume that
$j_\beta : \prod _{\alpha \in S} {\mathcal A}_\alpha \to {\mathcal A}_\beta $
. By enlarging S, if necessary, we may assume that
![]() $\mathrm {sup(S)\in S}$
. Let us denote
$\mathrm {sup(S)\in S}$
. Let us denote
![]() $\prod _{\alpha \in S}{\mathcal A}_\alpha $
by M. Notice that
$\prod _{\alpha \in S}{\mathcal A}_\alpha $
by M. Notice that
where
![]() $\overline {\in }$
is the pointwise membership relation, and
$\overline {\in }$
is the pointwise membership relation, and
![]() $\overline {R}^\alpha _\varphi $
is the pointwise
$\overline {R}^\alpha _\varphi $
is the pointwise
![]() $R^\alpha _\varphi $
relation. Let
$R^\alpha _\varphi $
relation. Let
![]() $\kappa := \mathrm {sup(S)}$
.
$\kappa := \mathrm {sup(S)}$
.
Now assume, aiming for a contradiction, that no cardinal
![]() $\leq\!\kappa $
is strong, and fix some
$\leq\!\kappa $
is strong, and fix some
![]() $\beta \in C$
greater than
$\beta \in C$
greater than
![]() $\kappa $
, of uncountable cofinality, such that no cardinal
$\kappa $
, of uncountable cofinality, such that no cardinal
![]() $\leq\!\kappa $
is
$\leq\!\kappa $
is
![]() $\beta $
-strong. Let
$\beta $
-strong. Let
![]() $j=j_\beta $
.⊣
$j=j_\beta $
.⊣
Claim 4.2 j preserves the Boolean operations
![]() $\cap $
,
$\cap $
,
![]() $\cup $
,
$\cup $
,
![]() $-$
, and also the
$-$
, and also the
![]() $\subseteq $
relation.
$\subseteq $
relation.
Proof of claim For every
![]() $X,Y,Z\in M$
,
$X,Y,Z\in M$
,
So, letting
![]() $\varphi (x,y,z)$
be the bounded formula expressing
$\varphi (x,y,z)$
be the bounded formula expressing
![]() $x=y\cap z$
, we have that
$x=y\cap z$
, we have that
![]() $\langle X(\alpha ),Y(\alpha ),Z(\alpha )\rangle \in R^\alpha _\varphi $
, for all
$\langle X(\alpha ),Y(\alpha ),Z(\alpha )\rangle \in R^\alpha _\varphi $
, for all
![]() $\alpha \in S$
. Hence
$\alpha \in S$
. Hence
![]() $\langle X,Y,Z\rangle \in \overline {R}_\varphi $
, and since j is a homomorphism
$\langle X,Y,Z\rangle \in \overline {R}_\varphi $
, and since j is a homomorphism
![]() $\langle j(X),j(Y),j(Z)\rangle \in R^\beta _\varphi $
, which yields
$\langle j(X),j(Y),j(Z)\rangle \in R^\beta _\varphi $
, which yields
![]() ${\mathcal A}_\beta \models “j(X)=j(Y)\cap j(Z).”$
${\mathcal A}_\beta \models “j(X)=j(Y)\cap j(Z).”$
Similarly for the operations
![]() $\cup , -$
, and for the relation
$\cup , -$
, and for the relation
![]() $\subseteq $
.
$\subseteq $
.
Now define
![]() $k:V_{\kappa +1}\to V_{\beta +1}$
by
$k:V_{\kappa +1}\to V_{\beta +1}$
by
Claim 4.3 k also preserves the Boolean operations, as well as the
![]() $\subseteq $
relation.
$\subseteq $
relation.
Proof of claim Suppose
![]() $V_{\kappa +1}\models “X=Y\cap Z.”$
Then
$V_{\kappa +1}\models “X=Y\cap Z.”$
Then
![]() $X\cap V_{\alpha } =(Y\cap V_{\alpha })\cap (Z\cap V_{\alpha })$
, for every
$X\cap V_{\alpha } =(Y\cap V_{\alpha })\cap (Z\cap V_{\alpha })$
, for every
![]() $\alpha \in S$
. Hence,
$\alpha \in S$
. Hence,
Since j preserves the
![]() $\cap $
operation,
$\cap $
operation,
Hence,
Similarly for the operations
![]() $\cup , -$
, and the relation
$\cup , -$
, and the relation
![]() $\subseteq $
.
$\subseteq $
.
Claim 4.4 k maps ordinals to ordinals, and is the identity on
![]() $\omega +1$
.
$\omega +1$
.
Proof of claim Let
![]() $\varphi (x)$
be the bounded formula expressing that x is an ordinal. Let
$\varphi (x)$
be the bounded formula expressing that x is an ordinal. Let
![]() $\gamma \leq \kappa $
. Then
$\gamma \leq \kappa $
. Then
![]() $\gamma \cap V_{\alpha }$
is an ordinal, for all
$\gamma \cap V_{\alpha }$
is an ordinal, for all
![]() $\alpha <\kappa $
, and so
$\alpha <\kappa $
, and so
Since j is a homomorphism,
which yields that
![]() $k(\gamma )=j(\langle \gamma \cap V_{\alpha }\rangle _{\alpha \in S})$
is an ordinal in
$k(\gamma )=j(\langle \gamma \cap V_{\alpha }\rangle _{\alpha \in S})$
is an ordinal in
![]() ${\mathcal A}_\beta $
, hence also in
${\mathcal A}_\beta $
, hence also in
![]() $V_{\beta +1}$
.
$V_{\beta +1}$
.
For every ordinal
![]() $\gamma \leq \omega $
, we have that
$\gamma \leq \omega $
, we have that
![]() $\gamma \cap V_{\alpha } =\gamma $
, for all
$\gamma \cap V_{\alpha } =\gamma $
, for all
![]() $\alpha \in S$
. Moreover,
$\alpha \in S$
. Moreover,
![]() $\gamma $
is definable by some bounded formula
$\gamma $
is definable by some bounded formula
![]() $\varphi _\gamma $
. Hence,
$\varphi _\gamma $
. Hence,
and therefore
which yields
![]() $k(\gamma )=\gamma $
.
$k(\gamma )=\gamma $
.
Note that
![]() $k(\kappa )=j(\langle \alpha \rangle _{\alpha \in S})= \beta $
.
$k(\kappa )=j(\langle \alpha \rangle _{\alpha \in S})= \beta $
.
For each
![]() $a\in [\beta ]^{<\omega }$
, define
$a\in [\beta ]^{<\omega }$
, define
![]() $E_a$
by
$E_a$
by
Since
![]() $k(\kappa )=\beta $
and
$k(\kappa )=\beta $
and
![]() $k(|a|)=|a|$
, we also have
$k(|a|)=|a|$
, we also have
![]() $k([\kappa ]^{|a|})=[\beta ]^{|a|}$
, and hence
$k([\kappa ]^{|a|})=[\beta ]^{|a|}$
, and hence
![]() ${[\kappa ]^{|a|} \in E_a}$
. Moreover, since k preserves Boolean operations and the
${[\kappa ]^{|a|} \in E_a}$
. Moreover, since k preserves Boolean operations and the
![]() $\subseteq $
relation,
$\subseteq $
relation,
![]() $E_a$
is an ultrafilter over
$E_a$
is an ultrafilter over
![]() $[\kappa ]^{|a|}$
.
$[\kappa ]^{|a|}$
.
Claim 4.5
![]() $E_a$
is
$E_a$
is
![]() $\omega _1$
-complete.
$\omega _1$
-complete.
Proof of claim Given
![]() $\{ X_n:n<\omega \}\subseteq E_a$
, let
$\{ X_n:n<\omega \}\subseteq E_a$
, let
![]() $Y=\{ \langle n,x\rangle : x\in X_n\}$
. So,
$Y=\{ \langle n,x\rangle : x\in X_n\}$
. So,
![]() $Y\subseteq V_\kappa $
. We can express that
$Y\subseteq V_\kappa $
. We can express that
![]() $X=\bigcap _{n<\omega }X_n$
by a bounded sentence
$X=\bigcap _{n<\omega }X_n$
by a bounded sentence
![]() $\varphi $
in the parameters X, Y, and
$\varphi $
in the parameters X, Y, and
![]() $\omega $
. Moreover, since
$\omega $
. Moreover, since
![]() $\alpha $
is a limit ordinal, for every
$\alpha $
is a limit ordinal, for every
![]() $\alpha \in S$
, the sentence
$\alpha \in S$
, the sentence
![]() $\varphi (X\cap V_{\alpha }, Y\cap V_{\alpha }, \omega )$
expresses that
$\varphi (X\cap V_{\alpha }, Y\cap V_{\alpha }, \omega )$
expresses that
![]() $X\cap V_{\alpha } =\bigcap _{n<\omega }X_n\cap V_{\alpha }$
. So,
$X\cap V_{\alpha } =\bigcap _{n<\omega }X_n\cap V_{\alpha }$
. So,
Since j is a homomorphism,
and so
![]() $\langle k(X),k(Y),k(\omega )\rangle $
satisfies
$\langle k(X),k(Y),k(\omega )\rangle $
satisfies
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $k(\omega )=\omega $
, we thus have
$k(\omega )=\omega $
, we thus have
![]() $k(X)=\bigcap _{n<\omega }k(X_n)$
. Hence,
$k(X)=\bigcap _{n<\omega }k(X_n)$
. Hence,
![]() $a\in k(X)$
, and so
$a\in k(X)$
, and so
![]() $X\in E_a$
.
$X\in E_a$
.
Let
![]() $\mathcal {E}:=\{ E_a: a\in [\beta ]^{<\omega }\}$
.
$\mathcal {E}:=\{ E_a: a\in [\beta ]^{<\omega }\}$
.
Claim 4.6
![]() $\mathcal {E}$
is normal. That is, whenever
$\mathcal {E}$
is normal. That is, whenever
![]() $a\in [\beta ]^{<\omega }$
and f is a function with domain
$a\in [\beta ]^{<\omega }$
and f is a function with domain
![]() $[\kappa ]^{|a|}$
such that
$[\kappa ]^{|a|}$
such that
![]() $\{ s\in [\kappa ]^{|a|}: f(s)\in {\mathrm {max}}(s)\}\in E_a$
, there is
$\{ s\in [\kappa ]^{|a|}: f(s)\in {\mathrm {max}}(s)\}\in E_a$
, there is
![]() $b\supseteq a$
such that
$b\supseteq a$
such that
![]() $\{ s\in [\kappa ]^{|b|}: f(\pi ^\kappa _{ba}(s))\in s\}\in E_{b}$
, where
$\{ s\in [\kappa ]^{|b|}: f(\pi ^\kappa _{ba}(s))\in s\}\in E_{b}$
, where
![]() $\pi ^\kappa _{ba}:[\kappa ]^{|b|}\to [\kappa ]^{|a|}$
is the standard projection function.
$\pi ^\kappa _{ba}:[\kappa ]^{|b|}\to [\kappa ]^{|a|}$
is the standard projection function.
Proof Fix a and f, and suppose the set
belongs to
![]() $E_a$
. For every
$E_a$
. For every
![]() $\alpha \in S$
,
$\alpha \in S$
,
Thus, letting
![]() $\varphi [X\cap V_\alpha , \alpha , |a|, f\cap V_\alpha ]$
be the sentence
$\varphi [X\cap V_\alpha , \alpha , |a|, f\cap V_\alpha ]$
be the sentence
we have that
Since the formula
![]() $\varphi (x,y,z)$
is equivalent to a bounded formula, we have
$\varphi (x,y,z)$
is equivalent to a bounded formula, we have
![]() $\langle X\cap V_\alpha , \alpha , |a|, f\cap V_\alpha \rangle \in R^\alpha _\varphi $
, for every
$\langle X\cap V_\alpha , \alpha , |a|, f\cap V_\alpha \rangle \in R^\alpha _\varphi $
, for every
![]() $\alpha \in S$
. Hence,
$\alpha \in S$
. Hence,
and therefore
Since
![]() $j(\langle \alpha \rangle _{\alpha \in S})=k(\kappa )=\beta $
and
$j(\langle \alpha \rangle _{\alpha \in S})=k(\kappa )=\beta $
and
![]() $k(|a|)=|a|$
,
$k(|a|)=|a|$
,
which yields
Also, since
![]() $X\in E_a$
, we have that
$X\in E_a$
, we have that
![]() $k(f)(a)\in \mathrm {max}(a)$
.
$k(f)(a)\in \mathrm {max}(a)$
.
Let
![]() $\delta =k(f)(a)$
, and let
$\delta =k(f)(a)$
, and let
![]() $b=a\cup \{ \delta \}$
. Thus,
$b=a\cup \{ \delta \}$
. Thus,
where
![]() $\pi ^\beta _{ba}:[\beta ]^{|b|}\to [\beta ]^{|a|}$
is the standard projection function. So, since
$\pi ^\beta _{ba}:[\beta ]^{|b|}\to [\beta ]^{|a|}$
is the standard projection function. So, since
![]() $\{ s\in [\beta ]^{|b|}: k(f)(\pi ^\beta _{ba}(s))\in s\}=k(\{ s\in [\kappa ]^{|b|}: f(\pi ^\kappa _{ba}(s))\in s\})$
, we have
$\{ s\in [\beta ]^{|b|}: k(f)(\pi ^\beta _{ba}(s))\in s\}=k(\{ s\in [\kappa ]^{|b|}: f(\pi ^\kappa _{ba}(s))\in s\})$
, we have
which shows that
![]() ${\mathcal E}$
is normal.
${\mathcal E}$
is normal.
For each
![]() $a\in [\beta ]^{<\omega }$
, the ultrapower
$a\in [\beta ]^{<\omega }$
, the ultrapower
![]() ${\mathrm {Ult}}(V,E_a)$
of V by the
${\mathrm {Ult}}(V,E_a)$
of V by the
![]() $\omega _1$
-complete ultrafilter
$\omega _1$
-complete ultrafilter
![]() $E_a$
is well-founded. So, let
$E_a$
is well-founded. So, let
with
![]() $M_a$
transitive, be the corresponding ultrapower embedding. As usual, we denote the elements of
$M_a$
transitive, be the corresponding ultrapower embedding. As usual, we denote the elements of
![]() $M_a$
by their corresponding elements in
$M_a$
by their corresponding elements in
![]() $\mathrm {Ult}(V, E_a)$
.
$\mathrm {Ult}(V, E_a)$
.
Claim 4.7
![]() $\mathcal {E}$
is coherent. That is, for every
$\mathcal {E}$
is coherent. That is, for every
![]() $a\subseteq b$
in
$a\subseteq b$
in
![]() $[\beta ]^{<\omega }$
,
$[\beta ]^{<\omega }$
,
Proof Let
![]() $a\subseteq b$
in
$a\subseteq b$
in
![]() $[\beta ]^{<\omega }$
, and suppose
$[\beta ]^{<\omega }$
, and suppose
![]() $X\in E_a$
. Thus,
$X\in E_a$
. Thus,
![]() $X\subseteq [\kappa ]^{|a|}$
and
$X\subseteq [\kappa ]^{|a|}$
and
![]() $a\in k(X)$
. We need to see that
$a\in k(X)$
. We need to see that
![]() $b\in k(\{ s\in [\kappa ]^{|b|}:\pi _{ba}(s) \in X\})$
. Now notice that, since k is the identity on natural numbers, and
$b\in k(\{ s\in [\kappa ]^{|b|}:\pi _{ba}(s) \in X\})$
. Now notice that, since k is the identity on natural numbers, and
![]() $k(\kappa )=\beta $
,
$k(\kappa )=\beta $
,
Hence, since
![]() $\pi _{ba}(b)=a$
, and
$\pi _{ba}(b)=a$
, and
![]() $a\in k(X)$
, we have that
$a\in k(X)$
, we have that
![]() $b\in \{ s\in [\beta ]^{|b|}: \pi _{ba}(s)\in k(X)\}$
, as wanted.
$b\in \{ s\in [\beta ]^{|b|}: \pi _{ba}(s)\in k(X)\}$
, as wanted.
Conversely, if
![]() $\{ s\in [\kappa ]^{|b|}: \pi _{ba}(s) \in X\}\in E_b$
, we have that
$\{ s\in [\kappa ]^{|b|}: \pi _{ba}(s) \in X\}\in E_b$
, we have that
![]() $b\in k(\{ s\in [\kappa ]^{|b|}:\pi _{ba}(s) \in X\})=\{ s\in [\beta ]^{|b|}: \pi _{ba}(s)\in k(X)\}.$
Hence,
$b\in k(\{ s\in [\kappa ]^{|b|}:\pi _{ba}(s) \in X\})=\{ s\in [\beta ]^{|b|}: \pi _{ba}(s)\in k(X)\}.$
Hence,
![]() $\pi _{ba}(b)=a\in k(X)$
, and therefore
$\pi _{ba}(b)=a\in k(X)$
, and therefore
![]() $X\in E_a$
.
$X\in E_a$
.
For each
![]() $a\subseteq b$
in
$a\subseteq b$
in
![]() $[\beta ]^{<\omega }$
, let
$[\beta ]^{<\omega }$
, let
![]() $i_{ab}:M_a\to M_b$
be given by
$i_{ab}:M_a\to M_b$
be given by
for all
![]() $f:[\kappa ]^{|a|}\to V$
. By coherence, the maps
$f:[\kappa ]^{|a|}\to V$
. By coherence, the maps
![]() $i_{ab}$
are well-defined and commute with the ultrapower embeddings
$i_{ab}$
are well-defined and commute with the ultrapower embeddings
![]() $j_a$
(see [Reference Kanamori9, Section 26]).
$j_a$
(see [Reference Kanamori9, Section 26]).
Let
![]() $M_{\mathcal E}$
be the direct limit of
$M_{\mathcal E}$
be the direct limit of
For notational simplicity, whenever we write
![]() $[a, [f]]$
what we mean is that
$[a, [f]]$
what we mean is that
![]() $[f]=[f]_{E_a}$
, which belongs to
$[f]=[f]_{E_a}$
, which belongs to
![]() $M_a$
. Thus, when we say, e.g., that
$M_a$
. Thus, when we say, e.g., that
![]() $[a, [f]]\in [b,[g]]$
in
$[a, [f]]\in [b,[g]]$
in
![]() $M_{\mathcal E}$
, what we mean is that
$M_{\mathcal E}$
, what we mean is that
![]() $[f]=[f]_{E_a}\in M_a$
,
$[f]=[f]_{E_a}\in M_a$
,
![]() $[g]=[g]_{E_b}\in M_b$
, and
$[g]=[g]_{E_b}\in M_b$
, and
![]() $[\langle a, [f]_{E_a}\rangle ]_{\mathcal E} \in _{\mathcal E} [\langle b, [g]_{E_b}\rangle ]_{\mathcal E}$
.
$[\langle a, [f]_{E_a}\rangle ]_{\mathcal E} \in _{\mathcal E} [\langle b, [g]_{E_b}\rangle ]_{\mathcal E}$
.
Let
![]() $j_{\mathcal E} :V\to M_{\mathcal E}$
be the corresponding limit elementary embedding, i.e.,
$j_{\mathcal E} :V\to M_{\mathcal E}$
be the corresponding limit elementary embedding, i.e.,
for some (any)
![]() $a\in [\beta ]^{<\omega }$
, and where
$a\in [\beta ]^{<\omega }$
, and where
![]() $c^a_x:[\kappa ]^{|a|}\to \{ x\}$
.
$c^a_x:[\kappa ]^{|a|}\to \{ x\}$
.
Let
![]() $k_a:M_a\to M_{\mathcal E}$
be given by
$k_a:M_a\to M_{\mathcal E}$
be given by
It is easily checked that
![]() $j_{\mathcal E} =k_a \circ j_a$
and
$j_{\mathcal E} =k_a \circ j_a$
and
![]() $k_b \circ i_{ab}=k_a$
, for all
$k_b \circ i_{ab}=k_a$
, for all
![]() $a\subseteq b$
,
$a\subseteq b$
,
![]() $a,b \in [\beta ]^{<\omega }$
. Thus, letting
$a,b \in [\beta ]^{<\omega }$
. Thus, letting
![]() $\mathrm {Id}_{|a|}: [\kappa ]^{|a|}\to [\kappa ]^{|a|}$
be the identity function, we have
$\mathrm {Id}_{|a|}: [\kappa ]^{|a|}\to [\kappa ]^{|a|}$
be the identity function, we have
Let
![]() $M^\ast _{\mathcal E} :=\{ [a,[f]]\in M_{\mathcal E} : f \cap V_{\alpha }: [\alpha ]^{|a|}\to V_{\alpha } , \mbox { all }\alpha \in S\}$
. Suppose
$M^\ast _{\mathcal E} :=\{ [a,[f]]\in M_{\mathcal E} : f \cap V_{\alpha }: [\alpha ]^{|a|}\to V_{\alpha } , \mbox { all }\alpha \in S\}$
. Suppose
![]() $[a,[f]], [b,[g]]\in M^\ast _{\mathcal E}$
. Then the following can be easily verified:
$[a,[f]], [b,[g]]\in M^\ast _{\mathcal E}$
. Then the following can be easily verified:
-
(1)
 $[a,[f]]\in _{\mathcal E} [b,[g]] \mbox { iff } k(f)(a)\in k(g)(b)$
.
$[a,[f]]\in _{\mathcal E} [b,[g]] \mbox { iff } k(f)(a)\in k(g)(b)$
. -
(2)
 $[a,[f]] =_{\mathcal E} [b,[g]] \mbox { iff } k(f)(a) = k(g)(b)$
.
$[a,[f]] =_{\mathcal E} [b,[g]] \mbox { iff } k(f)(a) = k(g)(b)$
.
Claim 4.8
![]() $M^\ast _{\mathcal E}$
is well-founded and downward closed under
$M^\ast _{\mathcal E}$
is well-founded and downward closed under
![]() $\in _{\mathcal E}$
.
$\in _{\mathcal E}$
.
Proof Well-foundedness follows from items (1) and (2) above, as any infinite
![]() $\in _{\mathcal E}$
-descending sequence in
$\in _{\mathcal E}$
-descending sequence in
![]() $M^\ast _{\mathcal E}$
would yield an infinite
$M^\ast _{\mathcal E}$
would yield an infinite
![]() $\in $
-descending sequence in
$\in $
-descending sequence in
![]() $V_{\beta +1}$
.
$V_{\beta +1}$
.
Now suppose
![]() $[a,[f]]\in _{\mathcal E} [b,[g]]$
, with
$[a,[f]]\in _{\mathcal E} [b,[g]]$
, with
![]() $[b,[g]]\in M^\ast _{\mathcal E}$
. Then, for some
$[b,[g]]\in M^\ast _{\mathcal E}$
. Then, for some
![]() $c\supseteq a,b$
, and some
$c\supseteq a,b$
, and some
![]() $X\in E_c$
,
$X\in E_c$
,
for every
![]() $s\in X$
. Let
$s\in X$
. Let
![]() $Y=\{ \pi _{ca}(s):s\in X\} \in E_a$
. Define
$Y=\{ \pi _{ca}(s):s\in X\} \in E_a$
. Define
![]() $h:[\kappa ]^{|a|}\to V$
by:
$h:[\kappa ]^{|a|}\to V$
by:
![]() $h(s)=f(s)$
for all
$h(s)=f(s)$
for all
![]() $s\in Y$
, and
$s\in Y$
, and
![]() $h(s)=0$
, otherwise. Then
$h(s)=0$
, otherwise. Then
![]() $[h]_{E_a}=[f]_{E_a}$
, and
$[h]_{E_a}=[f]_{E_a}$
, and
![]() $[a,[f]]=[a,[h]]\in M^\ast _{\mathcal E}$
.
$[a,[f]]=[a,[h]]\in M^\ast _{\mathcal E}$
.
By the last claim,
![]() $M^\ast _{\mathcal E}$
is well-founded and extensional. So, let
$M^\ast _{\mathcal E}$
is well-founded and extensional. So, let
![]() $M^\ast $
be the transitive collapse of
$M^\ast $
be the transitive collapse of
![]() $M^\ast _{\mathcal E}$
.
$M^\ast _{\mathcal E}$
.
Claim 4.9
![]() $V_\beta \subseteq M^\ast $
.
$V_\beta \subseteq M^\ast $
.
Proof of claim Since
![]() $\kappa $
and
$\kappa $
and
![]() $\alpha $
, for
$\alpha $
, for
![]() $\alpha \in S$
, belong to
$\alpha \in S$
, belong to
![]() $C^{(1)}$
, we have that
$C^{(1)}$
, we have that
![]() $|V_\kappa |=\kappa $
and
$|V_\kappa |=\kappa $
and
![]() $|V_{\alpha } |=\alpha $
, all
$|V_{\alpha } |=\alpha $
, all
![]() $\alpha \in S$
. Let
$\alpha \in S$
. Let
![]() $f\in V$
be a bijection between
$f\in V$
be a bijection between
![]() $[\kappa ]^1$
and
$[\kappa ]^1$
and
![]() $V_\kappa $
such that
$V_\kappa $
such that
![]() $f\restriction [\alpha ]^1$
is a bijection between
$f\restriction [\alpha ]^1$
is a bijection between
![]() $[\alpha ]^1$
and
$[\alpha ]^1$
and
![]() $V_{\alpha }$
, all
$V_{\alpha }$
, all
![]() $\alpha \in S$
. Let
$\alpha \in S$
. Let
![]() $\varphi (x,y,z)$
be a
$\varphi (x,y,z)$
be a
![]() $\Pi _1$
formula expressing that
$\Pi _1$
formula expressing that
![]() $x=[u]^1$
, with u an ordinal,
$x=[u]^1$
, with u an ordinal,
![]() $y=V_u$
, and
$y=V_u$
, and
![]() $z:x\to V_u$
is a bijection. Thus,
$z:x\to V_u$
is a bijection. Thus,
Hence,
and so
![]() $k(f): [\beta ]^1 \to V_\beta $
is a bijection. Therefore, for every
$k(f): [\beta ]^1 \to V_\beta $
is a bijection. Therefore, for every
![]() $x\in V_\beta $
there exists
$x\in V_\beta $
there exists
![]() $\gamma <\beta $
such that
$\gamma <\beta $
such that
![]() $k(f)(\{ \gamma \})=x$
.
$k(f)(\{ \gamma \})=x$
.
Thus, letting
![]() $D:=\{ [\{\gamma \}, [f]]:\gamma <\beta \}$
, we have just shown that the map
$D:=\{ [\{\gamma \}, [f]]:\gamma <\beta \}$
, we have just shown that the map
![]() $i:\langle D, \in _{\mathcal E} \restriction D\rangle \to \langle V_\beta , \in \rangle $
given by
$i:\langle D, \in _{\mathcal E} \restriction D\rangle \to \langle V_\beta , \in \rangle $
given by
is onto. Moreover, if
![]() $[\{ \gamma \},[f]]\in _{\mathcal E} [\{ \delta \},[f]]$
, then for some
$[\{ \gamma \},[f]]\in _{\mathcal E} [\{ \delta \},[f]]$
, then for some
![]() $X\in E_{\{\gamma ,\delta \} }$
, we have
$X\in E_{\{\gamma ,\delta \} }$
, we have
for every
![]() $s\in X$
. Letting
$s\in X$
. Letting
![]() $\varphi $
be the bounded formula expressing this, since
$\varphi $
be the bounded formula expressing this, since
![]() $V_{\alpha }$
is closed under f for every
$V_{\alpha }$
is closed under f for every
![]() $\alpha $
, we have
$\alpha $
, we have
Hence, in
![]() ${\mathcal A}_{\beta }$
, for every
${\mathcal A}_{\beta }$
, for every
![]() $s\in k(X)$
,
$s\in k(X)$
,
In particular, since
![]() $\{\gamma ,\delta \}\in k(X)$
,
$\{\gamma ,\delta \}\in k(X)$
,
A similar argument shows that i is one-to-one. Hence, i is an isomorphism, and so i is just the transitive collapsing map. Since
![]() $D\subseteq M^\ast _{\mathcal E}$
, to conclude that
$D\subseteq M^\ast _{\mathcal E}$
, to conclude that
![]() $V_\beta \subseteq M^\ast $
it will be sufficient to show that the transitive collapse of D is the same as the restriction to D of the transitive collapse of
$V_\beta \subseteq M^\ast $
it will be sufficient to show that the transitive collapse of D is the same as the restriction to D of the transitive collapse of
![]() $M^*_{\mathcal E}$
. For this, it suffices to see that every
$M^*_{\mathcal E}$
. For this, it suffices to see that every
![]() $\in _{\mathcal E}$
-element of an element of D is
$\in _{\mathcal E}$
-element of an element of D is
![]() $=_{\mathcal E}$
-equal to an element of D. So, suppose
$=_{\mathcal E}$
-equal to an element of D. So, suppose
![]() $[\{ \gamma \}, [f]]\in D$
and
$[\{ \gamma \}, [f]]\in D$
and
![]() $[a,[g]] \in _{\mathcal E} [\{\gamma \}, [f]]$
, with
$[a,[g]] \in _{\mathcal E} [\{\gamma \}, [f]]$
, with
![]() $[a,[g]] \in M^*_{\mathcal E}$
. Then
$[a,[g]] \in M^*_{\mathcal E}$
. Then
![]() $k(g)(a)\in k(f)({\gamma })$
, by (1) above (just before Claim 4.8). Now
$k(g)(a)\in k(f)({\gamma })$
, by (1) above (just before Claim 4.8). Now
![]() $k(f):[\beta ]^1\to V_\beta $
is surjective and
$k(f):[\beta ]^1\to V_\beta $
is surjective and
![]() $V_\beta $
is transitive, so there is some
$V_\beta $
is transitive, so there is some
![]() $\delta < \beta $
such that
$\delta < \beta $
such that
![]() $k(f)(\{\delta \})=k(g)(a)$
. Hence, by (2) above,
$k(f)(\{\delta \})=k(g)(a)$
. Hence, by (2) above,
![]() $[\{\delta \},[f]] =_{\mathcal E} [a,[g]]$
.
$[\{\delta \},[f]] =_{\mathcal E} [a,[g]]$
.
Claim 4.10
![]() $M_{\mathcal E}$
is closed under
$M_{\mathcal E}$
is closed under
![]() $\omega $
-sequences, and hence it is well-founded.
$\omega $
-sequences, and hence it is well-founded.
Proof of claim Let
![]() $\langle j_{\mathcal E} (f_n)(k_{a_n}([\mathrm {id}_{|a_n|}]_{E_{a_n}}))\rangle _{n<\omega }$
be a sequence of elements of
$\langle j_{\mathcal E} (f_n)(k_{a_n}([\mathrm {id}_{|a_n|}]_{E_{a_n}}))\rangle _{n<\omega }$
be a sequence of elements of
![]() $M_{\mathcal E}$
. On the one hand, the sequence
$M_{\mathcal E}$
. On the one hand, the sequence
![]() $\langle j_{\mathcal E} (f_n)\rangle _{n<\omega } =j_{\mathcal E}(\langle f_n\rangle _{n<\omega })$
belongs to
$\langle j_{\mathcal E} (f_n)\rangle _{n<\omega } =j_{\mathcal E}(\langle f_n\rangle _{n<\omega })$
belongs to
![]() $M_{\mathcal E}$
. On the other hand,
$M_{\mathcal E}$
. On the other hand,
![]() $k_{a_n}([\mathrm {Id}_{|a_n|}]_{E_{a_n}})=[a_n, [\mathrm {Id}_{|a_n|}]_{E_{a_n}}]$
belongs to
$k_{a_n}([\mathrm {Id}_{|a_n|}]_{E_{a_n}})=[a_n, [\mathrm {Id}_{|a_n|}]_{E_{a_n}}]$
belongs to
![]() $M^\ast _{\mathcal E}$
for all
$M^\ast _{\mathcal E}$
for all
![]() $n<\omega $
. Since
$n<\omega $
. Since
![]() ${\mathcal E}$
is normal (Claim 4.6), as in [Reference Kanamori9, Lemma 26.2(a)] we can show that the transitive collapse of
${\mathcal E}$
is normal (Claim 4.6), as in [Reference Kanamori9, Lemma 26.2(a)] we can show that the transitive collapse of
![]() $[a_n, [\mathrm {Id}_{|a_n|}]_{E_{a_n}}]$
is precisely
$[a_n, [\mathrm {Id}_{|a_n|}]_{E_{a_n}}]$
is precisely
![]() $a_n$
. The sequence
$a_n$
. The sequence
![]() $\langle a_n\rangle _{n<\omega }$
belongs to
$\langle a_n\rangle _{n<\omega }$
belongs to
![]() $V_\beta $
, because
$V_\beta $
, because
![]() $\beta $
has uncountable cofinality. Hence, since
$\beta $
has uncountable cofinality. Hence, since
![]() $V_\beta \subseteq M^\ast $
, the preimage of
$V_\beta \subseteq M^\ast $
, the preimage of
![]() $\langle a_n\rangle _{n<\omega }\in V_\beta $
under the transitive collapsing map of
$\langle a_n\rangle _{n<\omega }\in V_\beta $
under the transitive collapsing map of
![]() $M^\ast _{\mathcal E}$
to
$M^\ast _{\mathcal E}$
to
![]() $M^\ast $
is precisely the sequence
$M^\ast $
is precisely the sequence
![]() $\langle k_{a_n}([\mathrm {Id}_{|a_n|}]_{E_{a_n}})\rangle _{n<\omega }$
and belongs to
$\langle k_{a_n}([\mathrm {Id}_{|a_n|}]_{E_{a_n}})\rangle _{n<\omega }$
and belongs to
![]() $M_{\mathcal E}$
. It now follows that the sequence
$M_{\mathcal E}$
. It now follows that the sequence
![]() $\langle j_{\mathcal E} (f_n)(k_{a_n}([\mathrm {id}_{|a_n|}]_{E_{a_n}}))\rangle _{n<\omega }$
is also in
$\langle j_{\mathcal E} (f_n)(k_{a_n}([\mathrm {id}_{|a_n|}]_{E_{a_n}}))\rangle _{n<\omega }$
is also in
![]() $M_{\mathcal E}$
.
$M_{\mathcal E}$
.
Let
![]() $\pi :M_{\mathcal E} \to N$
be the transitive collapsing isomorphism, and let
$\pi :M_{\mathcal E} \to N$
be the transitive collapsing isomorphism, and let
![]() $j_N:V\to N$
be the corresponding elementary embedding, i.e.,
$j_N:V\to N$
be the corresponding elementary embedding, i.e.,
![]() $j_N=\pi \circ j_{\mathcal E}$
.
$j_N=\pi \circ j_{\mathcal E}$
.
Claim 4.11
![]() $j_N(\kappa )\geq \beta $
.
$j_N(\kappa )\geq \beta $
.
Proof of claim Let
![]() $\alpha <\beta $
. Let
$\alpha <\beta $
. Let
![]() $\mathrm {Id}_1$
be the identity function on
$\mathrm {Id}_1$
be the identity function on
![]() $[\kappa ]^1$
, and let
$[\kappa ]^1$
, and let
![]() $c_{[\kappa ]^1}:[\kappa ]^1 \to \{ [\kappa ]^1\}$
and
$c_{[\kappa ]^1}:[\kappa ]^1 \to \{ [\kappa ]^1\}$
and
![]() $c_\kappa :[\kappa ]^1\to \{ \kappa \}$
. In
$c_\kappa :[\kappa ]^1\to \{ \kappa \}$
. In
![]() $M_{\{ \alpha \}}$
, we have
$M_{\{ \alpha \}}$
, we have
and hence in
![]() $M_{\mathcal E}$
,
$M_{\mathcal E}$
,
and therefore, since
![]() $\pi (k_{\{ \alpha \}}([\mathrm {Id}_1]_{E_{\{ \alpha \}}}))=\{ \alpha \}$
, in N we have
$\pi (k_{\{ \alpha \}}([\mathrm {Id}_1]_{E_{\{ \alpha \}}}))=\{ \alpha \}$
, in N we have
that is,
![]() $\alpha <j_N(\kappa )$
.
$\alpha <j_N(\kappa )$
.
Since
![]() $\beta>\kappa $
, the last claim implies that the critical point of
$\beta>\kappa $
, the last claim implies that the critical point of
![]() $j_N$
is less than or equal to
$j_N$
is less than or equal to
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $V_\beta \subseteq N$
by Claim 4.9,
$V_\beta \subseteq N$
by Claim 4.9,
![]() $j_N$
witnesses that its critical point is a
$j_N$
witnesses that its critical point is a
![]() $\beta $
-strong cardinal, in contradiction to our choice of
$\beta $
-strong cardinal, in contradiction to our choice of
![]() $\beta $
. This completes the proof of Theorem 4.1.
$\beta $
. This completes the proof of Theorem 4.1.
The boldface version of Theorem 4.1, i.e., with parameters, also holds by essentially the same arguments. Namely,
Theorem 4.12. The following are equivalent:
-
(1) There exists a proper class of strong cardinals.
-
(2)
 $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(3)
 $\mathbf {\Pi _1}$
-
$\mathbf {\Pi _1}$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(4)
 $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(5)
 $\mathbf {\Pi _1}$
-
$\mathbf {\Pi _1}$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(6)
 $\mathbf {\Sigma _2}$
-
$\mathbf {\Sigma _2}$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
. -
(7)
 $\mathbf {\Pi _1}$
-
$\mathbf {\Pi _1}$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
For the proof of (3) implies (1), in order to show that there exists a strong cardinal greater than or equal to a fixed ordinal
![]() $\gamma $
we need to consider the class of structures
$\gamma $
we need to consider the class of structures
where the structure
is as in the proof of Theorem 4.1, and we have a constant
![]() $\delta $
for every
$\delta $
for every
![]() $\delta <\gamma $
.
$\delta <\gamma $
.
5 The general case
We shall now consider the general case of definable proper classes of structures with any degree of definable complexity. For this we shall need the following new kind of large cardinals.
If
![]() $j:V\to M$
is an elementary embedding, with M transitive and critical point
$j:V\to M$
is an elementary embedding, with M transitive and critical point
![]() $\kappa $
, and A is a class definable by a formula
$\kappa $
, and A is a class definable by a formula
![]() $\varphi $
(possibly with parameters in
$\varphi $
(possibly with parameters in
![]() $V_\kappa $
), we define
$V_\kappa $
), we define
Note that
as
![]() $j(A\cap V_\alpha )=\{ X \in M: M\models \varphi (X)\}\cap V^M_{j(\alpha )}$
. Also note that if A is a class of structures of the same type
$j(A\cap V_\alpha )=\{ X \in M: M\models \varphi (X)\}\cap V^M_{j(\alpha )}$
. Also note that if A is a class of structures of the same type
![]() $\tau \in V_\kappa $
, then by elementarity
$\tau \in V_\kappa $
, then by elementarity
![]() $j(A)$
is a subclass of M of structures of type
$j(A)$
is a subclass of M of structures of type
![]() $\tau $
.
$\tau $
.
5.1
 $\Gamma _n$
-strong cardinals
$\Gamma _n$
-strong cardinals
In the sequel, let
![]() $\Gamma _n$
stand for one of the definability classes
$\Gamma _n$
stand for one of the definability classes
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $\Pi _n$
.
$\Pi _n$
.
Definition 5.1. For
![]() $n\geq 1$
, a cardinal
$n\geq 1$
, a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Gamma _n$
-strong if for every
$\Gamma _n$
-strong if for every
![]() $\Gamma _n$
-definable (without parameters) class A there is an elementary embedding
$\Gamma _n$
-definable (without parameters) class A there is an elementary embedding
![]() $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $A\cap V_\lambda \subseteq j(A)$
.
$A\cap V_\lambda \subseteq j(A)$
.
![]() $\kappa $
is
$\kappa $
is
![]() $\Gamma _n$
-strong if it is
$\Gamma _n$
-strong if it is
![]() $\lambda $
-
$\lambda $
-
![]() $\Gamma _n$
-strong for every ordinal
$\Gamma _n$
-strong for every ordinal
![]() $\lambda $
.
$\lambda $
.
Note that in the definition above,
![]() $A \cap V_\lambda $
is only required to be contained in
$A \cap V_\lambda $
is only required to be contained in
![]() $j(A) \cap V_\lambda $
and not equal to it. The reason is that in the
$j(A) \cap V_\lambda $
and not equal to it. The reason is that in the
![]() $\Sigma _2$
case, if A is the class of non-strong cardinals (which is
$\Sigma _2$
case, if A is the class of non-strong cardinals (which is
![]() $\Sigma _2$
) and
$\Sigma _2$
) and
![]() $\kappa $
is the least strong cardinal, then
$\kappa $
is the least strong cardinal, then
![]() $\kappa \notin A$
, but
$\kappa \notin A$
, but
![]() $\kappa \in j(A)$
. See however the equivalence given in Proposition 5.9.
$\kappa \in j(A)$
. See however the equivalence given in Proposition 5.9.
As with the case of strong cardinals, standard arguments show (cf. [Reference Kanamori9, Exercise 26.7(b)]) that
![]() $\kappa $
is
$\kappa $
is
![]() $\Gamma _n$
-strong if and only if for every
$\Gamma _n$
-strong if and only if for every
![]() $\Gamma _n$
-definable (without parameters) class A and every ordinal
$\Gamma _n$
-definable (without parameters) class A and every ordinal
![]() $\lambda $
there is an elementary embedding
$\lambda $
there is an elementary embedding
![]() $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $A\cap V_\lambda \subseteq j(A)$
.
$A\cap V_\lambda \subseteq j(A)$
.
Proposition 5.2. Every strong cardinal is
![]() $\Sigma _2$
-strong.
$\Sigma _2$
-strong.
Proof Let
![]() $\kappa $
be a strong cardinal and let A be a class that is
$\kappa $
be a strong cardinal and let A be a class that is
![]() $\Sigma _2$
-definable (even allowing for parameters in
$\Sigma _2$
-definable (even allowing for parameters in
![]() $V_\kappa $
). Let
$V_\kappa $
). Let
![]() $\lambda \in C^{(2)}$
be greater than
$\lambda \in C^{(2)}$
be greater than
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $j:V\to M$
be elementary, with M transitive,
$j:V\to M$
be elementary, with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
, and
$\mathrm {crit}(j)=\kappa $
, and
![]() $V_\lambda \subseteq M$
. Let
$V_\lambda \subseteq M$
. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _2$
formula defining A. If
$\Sigma _2$
formula defining A. If
![]() $a\in A\cap V_\lambda $
, then
$a\in A\cap V_\lambda $
, then
![]() $V_\lambda \models \varphi (a)$
. Hence, since
$V_\lambda \models \varphi (a)$
. Hence, since
![]() $V_\lambda \preceq _{\Sigma _1}M$
,
$V_\lambda \preceq _{\Sigma _1}M$
,
![]() $M\models \varphi (a)$
, and so
$M\models \varphi (a)$
, and so
![]() $a\in j(A)=\{ x: M\models \varphi (x)\}$
.
$a\in j(A)=\{ x: M\models \varphi (x)\}$
.
Proposition 5.3. If
![]() $\lambda \in C^{(n+1)}$
, then a cardinal
$\lambda \in C^{(n+1)}$
, then a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Pi _n$
-strong if and only if it is
$\Pi _n$
-strong if and only if it is
![]() $\lambda $
-
$\lambda $
-
![]() $\Sigma _{n+1}$
-strong.
$\Sigma _{n+1}$
-strong.
Proof Assume
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Pi _n$
-strong, with
$\Pi _n$
-strong, with
![]() $\lambda \in C^{(n+1)}$
, and let A be a
$\lambda \in C^{(n+1)}$
, and let A be a
![]() $\Sigma _{n+1}$
-definable class. Let
$\Sigma _{n+1}$
-definable class. Let
![]() $\varphi (x)\equiv \exists y\, \psi (x,y)$
be a
$\varphi (x)\equiv \exists y\, \psi (x,y)$
be a
![]() $\Sigma _{n+1}$
formula, with
$\Sigma _{n+1}$
formula, with
![]() $\psi (x,y)$
being
$\psi (x,y)$
being
![]() $\Pi _n$
, that defines A. Now define B as the class of all structures of the form
$\Pi _n$
, that defines A. Now define B as the class of all structures of the form
![]() $\langle V_\alpha , \in , a\rangle $
, where
$\langle V_\alpha , \in , a\rangle $
, where
![]() $\alpha \in C^{(n)}$
,
$\alpha \in C^{(n)}$
,
![]() $a\in V_\alpha $
, and
$a\in V_\alpha $
, and
![]() $V_\alpha \models \varphi (a)$
. Then B is
$V_\alpha \models \varphi (a)$
. Then B is
![]() $\Pi _n$
-definable. By our assumption, let
$\Pi _n$
-definable. By our assumption, let
![]() $j:V\to M$
be an elementary embedding with M transitive,
$j:V\to M$
be an elementary embedding with M transitive,
![]() $\mathrm {crit} (j)=\kappa $
,
$\mathrm {crit} (j)=\kappa $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $B\cap V_\lambda \subseteq j(B)$
. We just need to show that
$B\cap V_\lambda \subseteq j(B)$
. We just need to show that
![]() $A\cap V_\lambda \subseteq j(A)$
. So, suppose
$A\cap V_\lambda \subseteq j(A)$
. So, suppose
![]() $a\in A\cap V_\lambda $
. Since
$a\in A\cap V_\lambda $
. Since
![]() $\lambda \in C^{(n+1)}$
, we have that
$\lambda \in C^{(n+1)}$
, we have that
![]() $V_\lambda \models \varphi (a)$
. Let
$V_\lambda \models \varphi (a)$
. Let
![]() $b\in V_\lambda $
be a witness, so that
$b\in V_\lambda $
be a witness, so that
![]() $V_\lambda \models \psi (a,b)$
. For some
$V_\lambda \models \psi (a,b)$
. For some
![]() $\alpha <\lambda $
in
$\alpha <\lambda $
in
![]() $C^{(n)}$
we have that
$C^{(n)}$
we have that
![]() $a, b\in V_\alpha $
. Hence,
$a, b\in V_\alpha $
. Hence,
![]() $V_\alpha \models \varphi (a)$
. So
$V_\alpha \models \varphi (a)$
. So
![]() $\langle V_\alpha , \in ,a\rangle \in B\cap V_\lambda $
, and therefore
$\langle V_\alpha , \in ,a\rangle \in B\cap V_\lambda $
, and therefore
![]() $\langle V_\alpha ,\in , a\rangle \in j(B)$
. Thus,
$\langle V_\alpha ,\in , a\rangle \in j(B)$
. Thus,
![]() $M\models “\alpha \in C^{(n)}, \, a\in V_\alpha , \mbox { and }V_\alpha \models \varphi (a).”$
Hence,
$M\models “\alpha \in C^{(n)}, \, a\in V_\alpha , \mbox { and }V_\alpha \models \varphi (a).”$
Hence,
![]() $M\models \varphi (a)$
, i.e.,
$M\models \varphi (a)$
, i.e.,
![]() $a\in j(A)$
.
$a\in j(A)$
.
Corollary 5.4. A cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi _n$
-strong if and only if it is
$\Pi _n$
-strong if and only if it is
![]() $\Sigma _{n+1}$
-strong.
$\Sigma _{n+1}$
-strong.
Proposition 5.5. Suppose that
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\lambda \in C^{(n)}$
. Then the following are equivalent for a cardinal
$\lambda \in C^{(n)}$
. Then the following are equivalent for a cardinal
![]() $\kappa <\lambda $
:
$\kappa <\lambda $
:
-
(1)
 $\kappa $
is
$\kappa $
is
 $\lambda $
-
$\lambda $
-
 $\Sigma _{n}$
-strong.
$\Sigma _{n}$
-strong. -
(2) There is an elementary embedding
 $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
 $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
 $V_\lambda \subseteq M$
,
$V_\lambda \subseteq M$
,
 $j(\kappa )>\lambda $
, and
$j(\kappa )>\lambda $
, and
 $M\models “\lambda \in C^{(n-1)}.”$
$M\models “\lambda \in C^{(n-1)}.”$
Proof (1)
![]() $\Rightarrow $
(2): Suppose
$\Rightarrow $
(2): Suppose
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Sigma _n$
-strong. Let
$\Sigma _n$
-strong. Let
![]() $A=C^{(n-1)}$
. Since A is
$A=C^{(n-1)}$
. Since A is
![]() $\Pi _{n-1}$
-definable, hence also
$\Pi _{n-1}$
-definable, hence also
![]() $\Sigma _n$
-definable, by (1) there is an elementary embedding
$\Sigma _n$
-definable, by (1) there is an elementary embedding
![]() $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
![]() $\mathrm {crit} (j)=\kappa $
,
$\mathrm {crit} (j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $A\cap V_\lambda \subseteq j(A)$
. Since
$A\cap V_\lambda \subseteq j(A)$
. Since
![]() $\lambda \in C^{(n)}$
,
$\lambda \in C^{(n)}$
,
![]() $C^{(n-1)}\cap \lambda $
is a club subset of
$C^{(n-1)}\cap \lambda $
is a club subset of
![]() $\lambda $
. For every
$\lambda $
. For every
![]() $\alpha <\lambda $
in
$\alpha <\lambda $
in
![]() $C^{(n-1)}$
,
$C^{(n-1)}$
,
![]() $\alpha \in j(A)$
, and hence
$\alpha \in j(A)$
, and hence
![]() $M\models “\alpha \in C^{(n-1)}”$
and so
$M\models “\alpha \in C^{(n-1)}”$
and so
![]() $M\models “\lambda \mbox { is a limit point of }C^{(n-1)},\!”$
which yields
$M\models “\lambda \mbox { is a limit point of }C^{(n-1)},\!”$
which yields
![]() $M\models “\lambda \in C^{(n-1)}.”$
$M\models “\lambda \in C^{(n-1)}.”$
(2)
![]() $\Rightarrow $
(1): Let A be a class definable by a
$\Rightarrow $
(1): Let A be a class definable by a
![]() $\Sigma _n$
formula
$\Sigma _n$
formula
![]() $\varphi $
, and let
$\varphi $
, and let
![]() $j:V\to M$
be an elementary embedding with M transitive,
$j:V\to M$
be an elementary embedding with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_{\lambda } \subseteq M$
, and
$V_{\lambda } \subseteq M$
, and
![]() $M\models “\lambda \in C^{(n-1)}.$
” Let
$M\models “\lambda \in C^{(n-1)}.$
” Let
![]() $a\in A\cap V_{\lambda }$
. Since
$a\in A\cap V_{\lambda }$
. Since
![]() $\lambda \in C^{(n)}$
,
$\lambda \in C^{(n)}$
,
![]() $V_{\lambda } \models \varphi (a)$
. And since
$V_{\lambda } \models \varphi (a)$
. And since
![]() $V_{\lambda } \subseteq M$
and
$V_{\lambda } \subseteq M$
and
![]() $M\models “\lambda \in C^{(n-1)},$
”
$M\models “\lambda \in C^{(n-1)},$
”
![]() $M\models \varphi (a)$
, i.e.,
$M\models \varphi (a)$
, i.e.,
![]() $a\in j(A)$
.
$a\in j(A)$
.
Proposition 5.6. If
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi _n$
-strong, then
$\Pi _n$
-strong, then
![]() $\kappa \in C^{(n+1)}$
.
$\kappa \in C^{(n+1)}$
.
Proof By induction on n. So let
![]() $\kappa $
be
$\kappa $
be
![]() $\Pi _n$
-strong and assume, inductively, that
$\Pi _n$
-strong and assume, inductively, that
![]() $\kappa \in C^{(n)}$
. Let
$\kappa \in C^{(n)}$
. Let
![]() $\exists x \varphi (x)$
be a formula, with
$\exists x \varphi (x)$
be a formula, with
![]() $\varphi (x)$
being a
$\varphi (x)$
being a
![]() $\Pi _n$
formula which may contain parameters in
$\Pi _n$
formula which may contain parameters in
![]() $V_\kappa $
, and suppose that
$V_\kappa $
, and suppose that
![]() $\exists x\varphi (x)$
holds in V. Pick a witness b and let
$\exists x\varphi (x)$
holds in V. Pick a witness b and let
![]() $\lambda \in C^{(n)}$
be such that
$\lambda \in C^{(n)}$
be such that
![]() $b\in V_\lambda $
. Thus,
$b\in V_\lambda $
. Thus,
![]() $V_\lambda \models \exists x \varphi (x)$
. By Corollary 5.4 and Proposition 5.5, let
$V_\lambda \models \exists x \varphi (x)$
. By Corollary 5.4 and Proposition 5.5, let
![]() $j:V\to M$
be an elementary embedding, with M transitive,
$j:V\to M$
be an elementary embedding, with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $V_\lambda \subseteq M$
,
$V_\lambda \subseteq M$
,
![]() $j(\kappa )>\lambda $
, and
$j(\kappa )>\lambda $
, and
![]() $M\models “\lambda \in C^{(n)}.”$
Then by elementarity of j, in V there exists some
$M\models “\lambda \in C^{(n)}.”$
Then by elementarity of j, in V there exists some
![]() $\lambda '\in C^{(n)}$
less than
$\lambda '\in C^{(n)}$
less than
![]() $\kappa $
such that
$\kappa $
such that
![]() $V_{\lambda '}\models “\exists x\varphi (x),\!”$
and since
$V_{\lambda '}\models “\exists x\varphi (x),\!”$
and since
![]() $\kappa \in C^{(n)}$
,
$\kappa \in C^{(n)}$
,
![]() $V_\kappa \models “\exists x \varphi (x),\!”$
as wanted.
$V_\kappa \models “\exists x \varphi (x),\!”$
as wanted.
The last proposition suggests the following definition and the ensuing characterization of
![]() $\Sigma _n$
-strong cardinals in terms of extenders.
$\Sigma _n$
-strong cardinals in terms of extenders.
Definition 5.7. Given
![]() $n\geq 1$
and given cardinals
$n\geq 1$
and given cardinals
![]() $\kappa <\lambda $
, a
$\kappa <\lambda $
, a
![]() $\Sigma _n$
-strong
$\Sigma _n$
-strong
![]() $(\kappa ,\lambda )$
-extender is a
$(\kappa ,\lambda )$
-extender is a
![]() $(\kappa ,|V_{\lambda }|^+)$
-extender
$(\kappa ,|V_{\lambda }|^+)$
-extender
![]() ${\mathcal E}$
(see Definition 2.3) such that
${\mathcal E}$
(see Definition 2.3) such that
![]() $V_{\lambda }\subseteq \overline {M}_{\mathcal {E}}$
,
$V_{\lambda }\subseteq \overline {M}_{\mathcal {E}}$
,
![]() $\lambda <j(\kappa )$
, and
$\lambda <j(\kappa )$
, and
![]() $\overline {M}_{\mathcal E}\models “\lambda \in C^{(n-1)},\!”$
where
$\overline {M}_{\mathcal E}\models “\lambda \in C^{(n-1)},\!”$
where
![]() $\overline {M}_{\mathcal E}$
is the transitive collapse of the direct limit ultrapower
$\overline {M}_{\mathcal E}$
is the transitive collapse of the direct limit ultrapower
![]() $M_{\mathcal E}$
of V by
$M_{\mathcal E}$
of V by
![]() ${\mathcal E}$
, and
${\mathcal E}$
, and
![]() $j:V\to \overline {M}_{\mathcal E}$
is the corresponding elementary embedding.
$j:V\to \overline {M}_{\mathcal E}$
is the corresponding elementary embedding.
Proposition 5.8. If
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\lambda \in C^{(n)}$
, then a cardinal
$\lambda \in C^{(n)}$
, then a cardinal
![]() $\kappa <\lambda $
is
$\kappa <\lambda $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Sigma _n$
-strong if and only if there exists a
$\Sigma _n$
-strong if and only if there exists a
![]() $\Sigma _n$
-strong
$\Sigma _n$
-strong
![]() $(\kappa , \lambda )$
-extender.
$(\kappa , \lambda )$
-extender.
Proof If
![]() ${\mathcal E}$
is a
${\mathcal E}$
is a
![]() $\Sigma _n$
-strong
$\Sigma _n$
-strong
![]() $(\kappa ,\lambda )$
-extender, then the extender embedding
$(\kappa ,\lambda )$
-extender, then the extender embedding
![]() $j:V\to \overline {M}_{\mathcal E}$
witnesses that
$j:V\to \overline {M}_{\mathcal E}$
witnesses that
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Sigma _n$
-strong by Proposition 5.5.
$\Sigma _n$
-strong by Proposition 5.5.
Conversely, suppose
![]() $j:V\to M$
is an elementary embedding, with M transitive,
$j:V\to M$
is an elementary embedding, with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $M\models “\lambda \in C^{(n-1)}.”$
Note that since
$M\models “\lambda \in C^{(n-1)}.”$
Note that since
![]() $\lambda \in C^{(1)}$
,
$\lambda \in C^{(1)}$
,
![]() $|V_\lambda |=\lambda $
. Let
$|V_\lambda |=\lambda $
. Let
![]() ${\mathcal E}$
be the
${\mathcal E}$
be the
![]() $(\kappa , \lambda ^+)$
-extender derived from j. Namely, for every
$(\kappa , \lambda ^+)$
-extender derived from j. Namely, for every
![]() $a\in [\lambda ^+]^{<\omega }$
let
$a\in [\lambda ^+]^{<\omega }$
let
![]() $E_a$
be defined by
$E_a$
be defined by
One can easily check that
![]() ${\mathcal E}$
satisfies conditions
${\mathcal E}$
satisfies conditions
![]() $(1)$
–
$(1)$
–
![]() $(5)$
of Definition 2.3 (see [Reference Kanamori9, Exercise 26.7]). So we only need to check that
$(5)$
of Definition 2.3 (see [Reference Kanamori9, Exercise 26.7]). So we only need to check that
![]() $\overline {M}_{\mathcal E}\models “\lambda \in C^{(n-1)}.”$
$\overline {M}_{\mathcal E}\models “\lambda \in C^{(n-1)}.”$
Let
![]() $j_{\mathcal E}:V\to M_{\mathcal E}$
and
$j_{\mathcal E}:V\to M_{\mathcal E}$
and
![]() $k_{\mathcal E}:\overline {M}_{\mathcal E}\to M$
be the standard maps given by:
$k_{\mathcal E}:\overline {M}_{\mathcal E}\to M$
be the standard maps given by:
![]() $j_{\mathcal E}(x)=[a, [c^a_x]]$
(any a), where
$j_{\mathcal E}(x)=[a, [c^a_x]]$
(any a), where
![]() $c^a_x :[\kappa ]^{|a|} \to \{ x\}$
; and
$c^a_x :[\kappa ]^{|a|} \to \{ x\}$
; and
![]() $k_{\mathcal E}(\pi ([a,[f]]))=j(f)(a)$
, for
$k_{\mathcal E}(\pi ([a,[f]]))=j(f)(a)$
, for
![]() $f:[\kappa ]^{|a|}\to V$
, where
$f:[\kappa ]^{|a|}\to V$
, where
![]() $\pi :M_{\mathcal E}\to \overline {M}_{\mathcal E}$
is the transitive collapse isomorphism. The maps
$\pi :M_{\mathcal E}\to \overline {M}_{\mathcal E}$
is the transitive collapse isomorphism. The maps
![]() $j_{\mathcal E}$
and
$j_{\mathcal E}$
and
![]() $k_{\mathcal E}$
are elementary and
$k_{\mathcal E}$
are elementary and
![]() $j=k_{\mathcal E} \circ \pi \circ j_{\mathcal E}$
. Moreover,
$j=k_{\mathcal E} \circ \pi \circ j_{\mathcal E}$
. Moreover,
![]() $k_{\mathcal E}\restriction V_\lambda $
is the identity.
$k_{\mathcal E}\restriction V_\lambda $
is the identity.
Since
![]() $M\models “\lambda \in C^{(n-1)},\!”$
for each
$M\models “\lambda \in C^{(n-1)},\!”$
for each
![]() $\mu <\lambda $
in
$\mu <\lambda $
in
![]() $C^{(n-1)}$
, we have that
$C^{(n-1)}$
, we have that
![]() $M\models “\mu \in C^{(n-1)}.”$
So, since
$M\models “\mu \in C^{(n-1)}.”$
So, since
![]() $k_{\mathcal E}$
is elementary and is the identity on
$k_{\mathcal E}$
is elementary and is the identity on
![]() $V_\lambda $
, we have that
$V_\lambda $
, we have that
![]() $M_{\mathcal E}\models “\mu \in C^{(n-1)}.”$
Hence,
$M_{\mathcal E}\models “\mu \in C^{(n-1)}.”$
Hence,
![]() $M_{\mathcal E}\models “\lambda \mbox { is a limit point of }C^{(n-1)},\!”$
which yields
$M_{\mathcal E}\models “\lambda \mbox { is a limit point of }C^{(n-1)},\!”$
which yields
![]() $M_{\mathcal E}\models “\lambda \in C^{(n-1)}.”$
$M_{\mathcal E}\models “\lambda \in C^{(n-1)}.”$
Similar characterizations may also be given for
![]() $\Pi _n$
-strong cardinals. Namely, if
$\Pi _n$
-strong cardinals. Namely, if
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $\lambda \in C^{(n)}$
, then a cardinal
$\lambda \in C^{(n)}$
, then a cardinal
![]() $\kappa <\lambda $
is
$\kappa <\lambda $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Pi _n$
-strong if and only if there exists a
$\Pi _n$
-strong if and only if there exists a
![]() $\Pi _n$
-strong
$\Pi _n$
-strong
![]() $(\kappa , \lambda )$
-extender. Notice that (3) of the following proposition characterizes
$(\kappa , \lambda )$
-extender. Notice that (3) of the following proposition characterizes
![]() $\Pi _n$
-strong cardinals as witnessing “
$\Pi _n$
-strong cardinals as witnessing “
![]() $\mathrm {OR}$
is Woodin” restricted to
$\mathrm {OR}$
is Woodin” restricted to
![]() $\Pi _n$
-definable classes (see Definition 5.14). In particular, it says
$\Pi _n$
-definable classes (see Definition 5.14). In particular, it says
![]() $A\cap V_\lambda = j(A)\cap V_\lambda $
, not just
$A\cap V_\lambda = j(A)\cap V_\lambda $
, not just
![]() $A\cap V_\lambda \subseteq j(A)\cap V_\lambda $
.
$A\cap V_\lambda \subseteq j(A)\cap V_\lambda $
.
Proposition 5.9. Suppose that
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $\lambda $
is a limit point of
$\lambda $
is a limit point of
![]() $C^{(n)}$
. Then the following are equivalent for a cardinal
$C^{(n)}$
. Then the following are equivalent for a cardinal
![]() $\kappa <\lambda $
:
$\kappa <\lambda $
:
-
(1)
 $\kappa $
is
$\kappa $
is
 $\lambda $
-
$\lambda $
-
 $\Pi _{n}$
-strong.
$\Pi _{n}$
-strong. -
(2) There is an elementary embedding
 $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
 $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
 $j(\kappa )=>\lambda $
,
$j(\kappa )=>\lambda $
,
 $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
 $M\models “\lambda \in C^{(n)}.”$
$M\models “\lambda \in C^{(n)}.”$
-
(3) For every
 $\Pi _n$
-definable class A there is an elementary embedding
$\Pi _n$
-definable class A there is an elementary embedding
 $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
 $\mathrm {crit} (j)=\kappa $
,
$\mathrm {crit} (j)=\kappa $
,
 $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
 $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
 $A\cap V_\lambda = j(A)\cap V_\lambda $
.
$A\cap V_\lambda = j(A)\cap V_\lambda $
.
Proof (1)
![]() $\Rightarrow $
(2): Suppose
$\Rightarrow $
(2): Suppose
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-
$\lambda $
-
![]() $\Pi _n$
-strong. Let
$\Pi _n$
-strong. Let
![]() $A=C^{(n)}$
. Since A is
$A=C^{(n)}$
. Since A is
![]() $\Pi _n$
-definable, by (1) there is an elementary embedding
$\Pi _n$
-definable, by (1) there is an elementary embedding
![]() $j:V\to M$
with M transitive,
$j:V\to M$
with M transitive,
![]() $\mathrm {crit} (j)=\kappa $
,
$\mathrm {crit} (j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $A\cap V_\lambda \subseteq j(A)$
. Thus, for every
$A\cap V_\lambda \subseteq j(A)$
. Thus, for every
![]() $\alpha <\lambda $
in A,
$\alpha <\lambda $
in A,
![]() $\alpha \in j(A)$
, and hence
$\alpha \in j(A)$
, and hence
![]() $M\models “\alpha \in C^{(n)}”$
and so
$M\models “\alpha \in C^{(n)}”$
and so
![]() $M\models “\lambda \mbox { is a limit point of }C^{(n)},\!”$
which yields
$M\models “\lambda \mbox { is a limit point of }C^{(n)},\!”$
which yields
![]() $M\models “\lambda \in C^{(n)}.”$
$M\models “\lambda \in C^{(n)}.”$
(2)
![]() $\Rightarrow $
(3): Let A be a class definable by a
$\Rightarrow $
(3): Let A be a class definable by a
![]() $\Pi _n$
formula
$\Pi _n$
formula
![]() $\varphi (x)$
, and let
$\varphi (x)$
, and let
![]() $j:V\to M$
be an elementary embedding with M transitive,
$j:V\to M$
be an elementary embedding with M transitive,
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $j(\kappa )>\lambda $
,
$j(\kappa )>\lambda $
,
![]() $V_\lambda \subseteq M$
, and
$V_\lambda \subseteq M$
, and
![]() $M\models “\lambda \in C^{(n)}.”$
Let
$M\models “\lambda \in C^{(n)}.”$
Let
![]() $a\in A\cap V_\lambda $
. Since
$a\in A\cap V_\lambda $
. Since
![]() $\lambda \in C^{(n)}$
,
$\lambda \in C^{(n)}$
,
![]() $V_\lambda \models \varphi (a)$
. And since
$V_\lambda \models \varphi (a)$
. And since
![]() $V_\lambda \subseteq M$
and
$V_\lambda \subseteq M$
and
![]() $M\models “\lambda \in C^{(n)},\!” M\models \varphi (a)$
, i.e.,
$M\models “\lambda \in C^{(n)},\!” M\models \varphi (a)$
, i.e.,
![]() $a\in j(A)$
. Conversely, suppose
$a\in j(A)$
. Conversely, suppose
![]() $a\in j(A)\cap V_\lambda $
, i.e.,
$a\in j(A)\cap V_\lambda $
, i.e.,
![]() $M\models “\varphi (a).”$
Since
$M\models “\varphi (a).”$
Since
![]() $M\models “\lambda \in C^{(n)},\!” V_\lambda \models \varphi (a)$
. And since
$M\models “\lambda \in C^{(n)},\!” V_\lambda \models \varphi (a)$
. And since
![]() $\lambda \in C^{(n)}$
,
$\lambda \in C^{(n)}$
,
![]() $a\in A$
.
$a\in A$
.
(3)
![]() $\Rightarrow $
(1) is immediate.
$\Rightarrow $
(1) is immediate.
Let us remark that the implication (2)
![]() $\Rightarrow $
(3) above also holds for classes A that are
$\Rightarrow $
(3) above also holds for classes A that are
![]() $\Pi _n$
-definable with parameters in
$\Pi _n$
-definable with parameters in
![]() $V_\kappa $
. Thus a corollary of Proposition 5.9 is that a cardinal
$V_\kappa $
. Thus a corollary of Proposition 5.9 is that a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi _n$
-strong if and only if it is
$\Pi _n$
-strong if and only if it is
![]() $\lambda $
-
$\lambda $
-
![]() $\Pi _n$
-strong for every
$\Pi _n$
-strong for every
![]() $\Pi _n$
-definable, with parameters in
$\Pi _n$
-definable, with parameters in
![]() $V_\kappa $
, class A.
$V_\kappa $
, class A.
It easily follows from the last proposition that being a
![]() $\Pi _n$
-strong cardinal is a
$\Pi _n$
-strong cardinal is a
![]() $\Pi _{n+1}$
property. Moreover, if
$\Pi _{n+1}$
property. Moreover, if
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi _n$
-strong, then
$\Pi _n$
-strong, then
![]() $\kappa \in C^{(n+1)}$
. Hence, if
$\kappa \in C^{(n+1)}$
. Hence, if
![]() $\kappa $
is
$\kappa $
is
![]() $\Pi _{n+1}$
-strong, then there are many
$\Pi _{n+1}$
-strong, then there are many
![]() $\Pi _n$
-strong cardinals below
$\Pi _n$
-strong cardinals below
![]() $\kappa $
, which shows that the
$\kappa $
, which shows that the
![]() $\Pi _n$
-strong cardinals,
$\Pi _n$
-strong cardinals,
![]() $n>0$
, form a hierarchy of strictly increasing strength.
$n>0$
, form a hierarchy of strictly increasing strength.
Similarly as in Proposition 3.3 we can prove the following.
Proposition 5.10. If
![]() $\kappa $
is a
$\kappa $
is a
![]() $\Sigma _n$
-strong cardinal, where
$\Sigma _n$
-strong cardinal, where
![]() $n\geq 2$
, then
$n\geq 2$
, then
![]() $\Sigma _n(V_\kappa )$
-
$\Sigma _n(V_\kappa )$
-
![]() $\mathrm {PRP}$
holds.
$\mathrm {PRP}$
holds.
Proof Let
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
![]() $\kappa $
be
$\kappa $
be
![]() $\Sigma _n$
-strong and let
$\Sigma _n$
-strong and let
![]() ${\mathcal C}$
be a definable, by a
${\mathcal C}$
be a definable, by a
![]() $\Sigma _n$
formula with parameters in
$\Sigma _n$
formula with parameters in
![]() $V_\kappa $
, proper class of structures in a fixed countable relational language. We will show that the set
$V_\kappa $
, proper class of structures in a fixed countable relational language. We will show that the set
![]() $S:={\mathcal C}\cap V_\kappa $
witnesses PRP.
$S:={\mathcal C}\cap V_\kappa $
witnesses PRP.
Given any
![]() ${\mathcal A}\in {\mathcal C}$
, let
${\mathcal A}\in {\mathcal C}$
, let
![]() $\lambda \geq \kappa $
be an ordinal with
$\lambda \geq \kappa $
be an ordinal with
![]() ${\mathcal A}\in V_\lambda $
.
${\mathcal A}\in V_\lambda $
.
Let
![]() $j:V\to M$
be an elementary embedding with
$j:V\to M$
be an elementary embedding with
![]() $\mathrm {crit}(j)=\kappa $
,
$\mathrm {crit}(j)=\kappa $
,
![]() $V_\lambda \subseteq M$
,
$V_\lambda \subseteq M$
,
![]() $j(\kappa )>\lambda $
, and
$j(\kappa )>\lambda $
, and
![]() ${\mathcal C}\cap V_\lambda \subseteq j({\mathcal C})$
.
${\mathcal C}\cap V_\lambda \subseteq j({\mathcal C})$
.
By elementarity, the restriction of j to
![]() $\prod S$
yields a homomorphism
$\prod S$
yields a homomorphism
Since
![]() ${\mathcal A}\in {\mathcal C} \cap V_\lambda $
, we have that
${\mathcal A}\in {\mathcal C} \cap V_\lambda $
, we have that
![]() ${\mathcal A} \in j({\mathcal C})$
. Moreover
${\mathcal A} \in j({\mathcal C})$
. Moreover
![]() ${\mathcal A} \in V_\lambda \subseteq V^M_{j(\kappa )}$
. Thus, letting
${\mathcal A} \in V_\lambda \subseteq V^M_{j(\kappa )}$
. Thus, letting
be the projection map, we have that
is a homomorphism, as wanted.
5.2 The main theorem for
 $\Gamma _n$
-strong cardinals
$\Gamma _n$
-strong cardinals
Using similar arguments as in Theorem 4.1, we can now prove the main theorem of this section.
Theorem 5.11. The following are equivalent for
![]() $n\geq 2$
:
$n\geq 2$
:
-
(1) There exists a
 $\Sigma _n$
-strong cardinal.
$\Sigma _n$
-strong cardinal. -
(2) There exists a
 $\Pi _{n-1}$
-strong cardinal.
$\Pi _{n-1}$
-strong cardinal. -
(3)
 $\Sigma _n$
-
$\Sigma _n$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(4)
 $\Pi _{n-1}$
-
$\Pi _{n-1}$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(5)
 $\Sigma _n$
-
$\Sigma _n$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(6)
 $\Pi _{n-1}$
-
$\Pi _{n-1}$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(7)
 $\Sigma _n$
-
$\Sigma _n$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
. -
(8)
 $\Pi _{n-1}$
-
$\Pi _{n-1}$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
Proof (1)
![]() $\Rightarrow $
(3) is given by Proposition 5.10. The equivalence of (3)–(8) is given by Theorem 3.7. So, we only need to prove (4)
$\Rightarrow $
(3) is given by Proposition 5.10. The equivalence of (3)–(8) is given by Theorem 3.7. So, we only need to prove (4)
![]() $\Rightarrow $
(2).
$\Rightarrow $
(2).
The proof is analogous to the proof of Theorem 4.1, so we shall only indicate the relevant differences. Theorem 4.1 proves the case
![]() $n=2$
(see Proposition 5.2). Thus, we shall assume in the sequel that
$n=2$
(see Proposition 5.2). Thus, we shall assume in the sequel that
![]() $n> 2$
.
$n> 2$
.
Let
![]() $\mathcal {A}$
be the class of all structures
$\mathcal {A}$
be the class of all structures
where the constant
![]() $\alpha $
is the
$\alpha $
is the
![]() $\alpha $
-th element of
$\alpha $
-th element of
![]() $C^{(n-1)}$
, and
$C^{(n-1)}$
, and
![]() $\{ R^{\alpha }_\varphi \}_{\varphi \in \Pi _1}$
is the
$\{ R^{\alpha }_\varphi \}_{\varphi \in \Pi _1}$
is the
![]() $\Pi _1$
relational diagram for
$\Pi _1$
relational diagram for
![]() $V_{\alpha +1}$
, i.e., if
$V_{\alpha +1}$
, i.e., if
![]() $\varphi (x_1,\ldots ,x_n)$
is a
$\varphi (x_1,\ldots ,x_n)$
is a
![]() $\Pi _1$
formula in the language of
$\Pi _1$
formula in the language of
![]() ${\langle V_{\alpha +1},\in ,\alpha , C^{(n-1)}\cap \alpha \rangle }$
, then
${\langle V_{\alpha +1},\in ,\alpha , C^{(n-1)}\cap \alpha \rangle }$
, then
Then
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\Pi _{n-1}$
-definable without parameters. For
$\Pi _{n-1}$
-definable without parameters. For
![]() $X\in \mathcal {A}$
if and only if
$X\in \mathcal {A}$
if and only if
![]() ${X=\langle X_0,X_1,X_2,X_3, X_4 \rangle }$
, where:
${X=\langle X_0,X_1,X_2,X_3, X_4 \rangle }$
, where:
-
(1)
 $X_2$
belongs to
$X_2$
belongs to
 $C^{(n-1)}$
.
$C^{(n-1)}$
. -
(2)
 $X_0=V_{X_2 +1}$
.
$X_0=V_{X_2 +1}$
. -
(3)
 $X_1 = \mathord {\in } \restriction X_0$
.
$X_1 = \mathord {\in } \restriction X_0$
. -
(4)
 $X_0$
satisfies that
$X_0$
satisfies that
 $X_3=C^{(n-1)}\cap X_2$
.
$X_3=C^{(n-1)}\cap X_2$
. -
(5)
 $X_4$
is the
$X_4$
is the
 $\Pi _1$
relational diagram of
$\Pi _1$
relational diagram of
 $\langle X_0,X_1,X_2,X_3 \rangle $
.
$\langle X_0,X_1,X_2,X_3 \rangle $
. -
(6)
 $\langle X_0, X_1, X_2, X_3 \rangle \models “X_2$
is the
$\langle X_0, X_1, X_2, X_3 \rangle \models “X_2$
is the
 $X_2$
-th element of
$X_2$
-th element of
 $C^{(n-1)}$
.”
$C^{(n-1)}$
.”
Note that the class C of ordinals
![]() $\alpha $
such that
$\alpha $
such that
![]() ${\mathcal A}_\alpha \in {\mathcal A}$
is a closed and unbounded proper class. By
${\mathcal A}_\alpha \in {\mathcal A}$
is a closed and unbounded proper class. By
![]() $\Pi _{n-1}$
-
$\Pi _{n-1}$
-
![]() $\mathrm {PRP}$
there exists a subset S of C such that for every
$\mathrm {PRP}$
there exists a subset S of C such that for every
![]() $\beta \in C$
there is a homomorphism
$\beta \in C$
there is a homomorphism
![]() $j_\beta : \prod _{\alpha \in S} {\mathcal A}_\alpha \to {\mathcal A}_\beta $
. By enlarging S, if necessary, we may assume that
$j_\beta : \prod _{\alpha \in S} {\mathcal A}_\alpha \to {\mathcal A}_\beta $
. By enlarging S, if necessary, we may assume that
![]() $\kappa := \mathrm {sup(S)\in S}$
.
$\kappa := \mathrm {sup(S)\in S}$
.
Now fix some
![]() $\beta \in C$
greater than
$\beta \in C$
greater than
![]() $\kappa $
, of uncountable cofinality, and assume, towards a contradiction, that no cardinal
$\kappa $
, of uncountable cofinality, and assume, towards a contradiction, that no cardinal
![]() $\leq\!\kappa $
is
$\leq\!\kappa $
is
![]() $\beta $
-
$\beta $
-
![]() $\Pi _{n-1}$
-strong. Let
$\Pi _{n-1}$
-strong. Let
![]() $j=j_\beta $
.
$j=j_\beta $
.
From this point, the proof proceeds as in Theorem 4.1. Namely, we define
![]() ${k:V_{\kappa +1}\to V_{\beta +1}}$
by
${k:V_{\kappa +1}\to V_{\beta +1}}$
by
and note that
![]() $k(\kappa ) =\beta $
.
$k(\kappa ) =\beta $
.
For each
![]() $a\in [\beta ]^{<\omega }$
, define
$a\in [\beta ]^{<\omega }$
, define
![]() $E_a$
by
$E_a$
by
As in Theorem 4.1,
![]() $E_a$
is an
$E_a$
is an
![]() $\omega _1$
-complete ultrafilter over
$\omega _1$
-complete ultrafilter over
![]() $[\kappa ]^{|a|}$
. Moreover,
$[\kappa ]^{|a|}$
. Moreover,
![]() ${\mathcal E} :=\{ E_a: a\in [\beta ]^{<\omega }\}$
is normal and coherent.
${\mathcal E} :=\{ E_a: a\in [\beta ]^{<\omega }\}$
is normal and coherent.
For each
![]() $a\in [\beta ]^{<\omega }$
, the ultrapower
$a\in [\beta ]^{<\omega }$
, the ultrapower
![]() ${\mathrm {Ult}}(V,E_a)$
is well-founded by
${\mathrm {Ult}}(V,E_a)$
is well-founded by
![]() $\omega _1$
-completeness. So, let
$\omega _1$
-completeness. So, let
with
![]() $M_a$
transitive, be the corresponding ultrapower embedding, and let
$M_a$
transitive, be the corresponding ultrapower embedding, and let
![]() $M_{\mathcal E}$
be the direct limit of
$M_{\mathcal E}$
be the direct limit of
where the
![]() $i_{ab}:M_a\to M_b$
are the usual commuting maps. The corresponding limit embedding
$i_{ab}:M_a\to M_b$
are the usual commuting maps. The corresponding limit embedding
![]() $j_{\mathcal E}:V\to M_{\mathcal E}$
is elementary. As in Theorem 4.1,
$j_{\mathcal E}:V\to M_{\mathcal E}$
is elementary. As in Theorem 4.1,
![]() $M_{\mathcal E}$
is closed under
$M_{\mathcal E}$
is closed under
![]() $\omega $
-sequences, and hence it is well-founded. Moreover, letting
$\omega $
-sequences, and hence it is well-founded. Moreover, letting
![]() $\pi :M_{\mathcal E} \to N$
be the transitive collapsing isomorphism, and
$\pi :M_{\mathcal E} \to N$
be the transitive collapsing isomorphism, and
![]() $j_N:V\to N$
the corresponding elementary embedding, i.e.,
$j_N:V\to N$
the corresponding elementary embedding, i.e.,
![]() $j_N=\pi \circ j_{\mathcal E}$
, we have that
$j_N=\pi \circ j_{\mathcal E}$
, we have that
![]() $V_\beta \subseteq N$
and
$V_\beta \subseteq N$
and
![]() $j_N(\kappa )\geq \beta $
. Since
$j_N(\kappa )\geq \beta $
. Since
![]() $\beta>\kappa $
, this implies that the critical point of
$\beta>\kappa $
, this implies that the critical point of
![]() $j_N$
is less than or equal to
$j_N$
is less than or equal to
![]() $\kappa $
. The only additional argument needed, with respect to the proof of Theorem 4.1, is the following:
$\kappa $
. The only additional argument needed, with respect to the proof of Theorem 4.1, is the following:
Claim 5.12
![]() $N\models “\beta \in C^{(n-1)}.”$
$N\models “\beta \in C^{(n-1)}.”$
Proof Since
![]() $\beta $
is a limit point of
$\beta $
is a limit point of
![]() $C^{(n-1)}$
, it suffices to show that if
$C^{(n-1)}$
, it suffices to show that if
![]() $\gamma <\beta $
belongs to
$\gamma <\beta $
belongs to
![]() $C^{(n-1)}$
, then
$C^{(n-1)}$
, then
![]() $N\models “\gamma \in C^{(n-1)}.”$
So, fix some
$N\models “\gamma \in C^{(n-1)}.”$
So, fix some
![]() $\gamma <\beta $
in
$\gamma <\beta $
in
![]() $C^{(n-1)}$
.
$C^{(n-1)}$
.
Let
![]() $f :[\kappa ]^1\to \kappa $
be such that
$f :[\kappa ]^1\to \kappa $
be such that
![]() $f (\{ x\})=x$
. It is well known that
$f (\{ x\})=x$
. It is well known that
![]() $k_{\{ \gamma \}}( [f]_{E_{\{\gamma \}}})=\gamma $
, where
$k_{\{ \gamma \}}( [f]_{E_{\{\gamma \}}})=\gamma $
, where
![]() $k_{\{ \gamma \}}:M_{\{\gamma \}}\to N$
is the standard map given by
$k_{\{ \gamma \}}:M_{\{\gamma \}}\to N$
is the standard map given by
![]() $k_{\{ \gamma \}}([f]_{E_{\{\gamma \}}})=\pi ([\{ \gamma \}, [f]_{E_{\{\gamma \}}}])$
(see [Reference Kanamori9, Lemma 26.2(a)]).
$k_{\{ \gamma \}}([f]_{E_{\{\gamma \}}})=\pi ([\{ \gamma \}, [f]_{E_{\{\gamma \}}}])$
(see [Reference Kanamori9, Lemma 26.2(a)]).
Let
![]() $X:=\{ \{ x\}\in [\kappa ]^1: x\in C^{(n-1)}\}$
. Note that, since being a singleton is a property expressible by a bounded formula, and
$X:=\{ \{ x\}\in [\kappa ]^1: x\in C^{(n-1)}\}$
. Note that, since being a singleton is a property expressible by a bounded formula, and
![]() $C^{(n-1)}\cap \alpha $
is a predicate in the language of every structure
$C^{(n-1)}\cap \alpha $
is a predicate in the language of every structure
![]() ${\mathcal A}_{\alpha }$
, the homomorphism k maps X to the set
${\mathcal A}_{\alpha }$
, the homomorphism k maps X to the set
![]() $\{\{ x\}\in [\beta ]^1: x\in C^{(n-1)}\}$
. Thus,
$\{\{ x\}\in [\beta ]^1: x\in C^{(n-1)}\}$
. Thus,
![]() $\{ \gamma \} \in k(X)$
, and therefore
$\{ \gamma \} \in k(X)$
, and therefore
![]() $X\in E_{\{\gamma \}}$
. Hence,
$X\in E_{\{\gamma \}}$
. Hence,
![]() $M_{\{ \gamma \}}\models “[f]\in C^{(n-1)},\!”$
and therefore
$M_{\{ \gamma \}}\models “[f]\in C^{(n-1)},\!”$
and therefore
![]() $M_{\mathcal E} \models “[\{ \gamma \}, [f]]\in C^{(n-1)},\!”$
which yields
$M_{\mathcal E} \models “[\{ \gamma \}, [f]]\in C^{(n-1)},\!”$
which yields
![]() $N\models “\gamma \in C^{(n-1)},\!”$
as wanted.
$N\models “\gamma \in C^{(n-1)},\!”$
as wanted.
Thus, by Proposition 5.9,
![]() $j_N$
witnesses that the critical point of
$j_N$
witnesses that the critical point of
![]() $j_N$
is less than or equal to
$j_N$
is less than or equal to
![]() $\kappa $
and is
$\kappa $
and is
![]() $\beta $
-
$\beta $
-
![]() $\Pi _{n-1}$
-strong, in contradiction to our choice of
$\Pi _{n-1}$
-strong, in contradiction to our choice of
![]() $\beta $
.
$\beta $
.
In a similar way we may obtain the following parameterized version of Theorem 5.11. For the proof of (4) implies (2), we need to consider the class of structures
where the structure
is as in the proof of Theorem 5.11, and we have a constant
![]() $\delta $
for every
$\delta $
for every
![]() $\delta <\gamma $
.
$\delta <\gamma $
.
Theorem 5.13. The following are equivalent for
![]() $n\geq 2$
:
$n\geq 2$
:
-
(1) There exists a proper class of
 $\ \Sigma _n$
-strong cardinals.
$\ \Sigma _n$
-strong cardinals. -
(2) There exists a proper class of
 $\ \Pi _{n-1}$
-strong cardinals.
$\ \Pi _{n-1}$
-strong cardinals. -
(3)
 $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(4)
 $\mathbf {\Pi _{n-1}}$
-
$\mathbf {\Pi _{n-1}}$
-
 $\mathrm {PRP}$
.
$\mathrm {PRP}$
. -
(5)
 $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(6)
 $\mathbf {\Pi _{n-1}}$
-
$\mathbf {\Pi _{n-1}}$
-
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(7)
 $\mathbf {\Sigma _n}$
-
$\mathbf {\Sigma _n}$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
. -
(8)
 $\mathbf {\Pi _{n-1}}$
-
$\mathbf {\Pi _{n-1}}$
-
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
Recall that a cardinal
![]() $\kappa $
is Woodin if for every
$\kappa $
is Woodin if for every
![]() $A\subseteq V_\kappa $
there is
$A\subseteq V_\kappa $
there is
![]() $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
![]() $\alpha $
is
$\alpha $
is
![]() $<\!\kappa $
-A-strong, i.e., for every
$<\!\kappa $
-A-strong, i.e., for every
![]() $\gamma <\kappa $
there is an elementary embedding
$\gamma <\kappa $
there is an elementary embedding
![]() $j:V\to M$
with
$j:V\to M$
with
![]() $\mathrm {crit} (j)=\alpha $
,
$\mathrm {crit} (j)=\alpha $
,
![]() $\gamma <j(\alpha )$
,
$\gamma <j(\alpha )$
,
![]() $V_\gamma \subseteq M$
, and
$V_\gamma \subseteq M$
, and
![]() $A\cap V_\gamma =j(A)\cap V_\gamma $
. (See [Reference Kanamori9, Theorem 26.14].)
$A\cap V_\gamma =j(A)\cap V_\gamma $
. (See [Reference Kanamori9, Theorem 26.14].)
Definition 5.14.
![]() $\mathrm {OR}$
is Woodin if for every definable (with set parameters) class A there exists some
$\mathrm {OR}$
is Woodin if for every definable (with set parameters) class A there exists some
![]() $\alpha $
which is A-strong, i.e., for every
$\alpha $
which is A-strong, i.e., for every
![]() $\gamma $
there is an elementary embedding
$\gamma $
there is an elementary embedding
![]() $j:V\to M$
with
$j:V\to M$
with
![]() $\mathrm {crit} (j)=\alpha $
,
$\mathrm {crit} (j)=\alpha $
,
![]() $\gamma <j(\alpha )$
,
$\gamma <j(\alpha )$
,
![]() $V_\gamma \subseteq M$
, and
$V_\gamma \subseteq M$
, and
![]() $A\cap V_\gamma =j(A)\cap V_\gamma $
.
$A\cap V_\gamma =j(A)\cap V_\gamma $
.
The statement “
![]() $\mathrm {OR}$
is Woodin” is first-order expressible as a schema, namely as “There exists
$\mathrm {OR}$
is Woodin” is first-order expressible as a schema, namely as “There exists
![]() $\alpha $
which is A-strong,” for each definable, with parameters, class A. Or equivalently, by Proposition 5.9 and the remark that follows it, as the schema “There exists
$\alpha $
which is A-strong,” for each definable, with parameters, class A. Or equivalently, by Proposition 5.9 and the remark that follows it, as the schema “There exists
![]() $\alpha $
which is
$\alpha $
which is
![]() $\Pi _n$
-strong,” for every n. Let us note that, by Theorem 5.13, “
$\Pi _n$
-strong,” for every n. Let us note that, by Theorem 5.13, “
![]() $\mathrm {OR}$
is Woodin” is also equivalent to the schema asserting “There exist a proper class of
$\mathrm {OR}$
is Woodin” is also equivalent to the schema asserting “There exist a proper class of
![]() $\alpha $
which are
$\alpha $
which are
![]() $\Pi _n$
-strong,” for every n. Thus, Theorem 5.13 yields the following corollary, first proved by the second author in [Reference Wilson13] for arbitrary classes (not necessarily definable), which gives the exact large-cardinal strength of
$\Pi _n$
-strong,” for every n. Thus, Theorem 5.13 yields the following corollary, first proved by the second author in [Reference Wilson13] for arbitrary classes (not necessarily definable), which gives the exact large-cardinal strength of
![]() $\mathrm {WVP}$
and
$\mathrm {WVP}$
and
![]() $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
.
Corollary 5.15. The following are equivalent:
-
(1)
 $\mathrm {OR}$
is Woodin.
$\mathrm {OR}$
is Woodin. -
(2)
 $\mathrm {SWVP}$
.
$\mathrm {SWVP}$
. -
(3)
 $\mathrm {WVP}$
.
$\mathrm {WVP}$
.
Acknowledgments
Part of this research was supported by the Generalitat de Catalunya (Catalan Government) under Grant No. SGR 270-2017, and by the Spanish Government under Grant No. MTM-PID2020-116773GB-I00.