Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ben-David, Shai
and
Shelah, Saharon
1986.
Souslin trees and successors of singular cardinals.
Annals of Pure and Applied Logic,
Vol. 30,
Issue. 3,
p.
207.
LaBerge, Tim
and
Landver, Avner
1995.
Tightness in products of fans and psuedo-fans.
Topology and its Applications,
Vol. 65,
Issue. 3,
p.
237.
Schimmerling, Ernest
1995.
Combinatorial principles in the core model for one Woodin cardinal.
Annals of Pure and Applied Logic,
Vol. 74,
Issue. 2,
p.
153.
Lipparini, Paolo
1996.
Ultrafilter translations.
Archive for Mathematical Logic,
Vol. 35,
Issue. 2,
p.
63.
Ben-David, Shai
and
Shelah, Saharon
1996.
The two-cardinals transfer property and resurrection of supercompactness span style=color:redThis article has been retracted/span.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 9,
p.
2827.
Schimmerling, E.
1998.
Set Theory.
p.
207.
Apter, Arthur W.
and
Cummings, James
2000.
A global version of a theorem of Ben-David and Magidor.
Annals of Pure and Applied Logic,
Vol. 102,
Issue. 3,
p.
199.
CUMMINGS, JAMES
FOREMAN, MATTHEW
and
MAGIDOR, MENACHEM
2001.
SQUARES, SCALES AND STATIONARY REFLECTION.
Journal of Mathematical Logic,
Vol. 01,
Issue. 01,
p.
35.
Cummings, James
and
Schimmerling, Ernest
2002.
Indexed squares.
Israel Journal of Mathematics,
Vol. 131,
Issue. 1,
p.
61.
SCHIMMERLING, ERNEST
and
ZEMAN, MARTIN
2004.
CHARACTERIZATION OF □κ IN CORE MODELS.
Journal of Mathematical Logic,
Vol. 04,
Issue. 01,
p.
1.
Gitik, Moti
and
Sharon, Assaf
2007.
On SCH and the approachability property.
Proceedings of the American Mathematical Society,
Vol. 136,
Issue. 1,
p.
311.
Juhász, István
Soukup, Lajos
and
Szentmiklóssy, Zoltán
2008.
Resolvability and monotone normality.
Israel Journal of Mathematics,
Vol. 166,
Issue. 1,
p.
1.
Welch, Philip D.
2010.
Handbook of Set Theory.
p.
657.
Eisworth, Todd
2010.
Club-guessing, stationary reflection, and coloring theorems.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 10,
p.
1216.
Lipparini, Paolo
2010.
More on regular and decomposable ultrafilters in ZFC.
Mathematical Logic Quarterly,
Vol. 56,
Issue. 4,
p.
340.
Eisworth, Todd
2010.
Handbook of Set Theory.
p.
1229.
Juhász, Istvan
and
Magidor, Menachem
2012.
On the maximal resolvability of monotonically normal spaces.
Israel Journal of Mathematics,
Vol. 192,
Issue. 2,
p.
637.
Lipparini, Paolo
2016.
Ultrafilter Convergence in Ordered Topological Spaces.
Order,
Vol. 33,
Issue. 2,
p.
269.
Shi, Xianghui
and
Trang, Nam
2017.
$$I_0$$ and combinatorics at $$\lambda ^+$$.
Archive for Mathematical Logic,
Vol. 56,
Issue. 1-2,
p.
131.
Zeman, Martin
2017.
Two Upper Bounds on Consistency Strength of ¬□ℵω and Stationary Set Reflection at Two Successive ℵn.
Notre Dame Journal of Formal Logic,
Vol. 58,
Issue. 3,


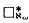 does not imply
does not imply 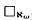 . The model-theoretic transfer property ⟨ℵ
. The model-theoretic transfer property ⟨ℵ