Article contents
The universal complementation property
Published online by Cambridge University Press: 12 March 2014
Extract
Let V∞ be a fully effective infinite dimensional vector space over a recursive field F. That is, we assume that the universe of V∞ is a recursive set, the operations of addition and scalar multiplication are recursive, and there is a uniform effective procedure to decide whether any finite set {υ0, …, υn} of vectors from V∞ is independent. The lattice 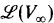 of recursively enumerable subspaces has been extensively studied since its introduction by Metakides and Nerode [MN1] (see for example, [Do2], [Gu], [KR], [Re1], [Re2], and [Sh]). For those unfamiliar with the literature on
of recursively enumerable subspaces has been extensively studied since its introduction by Metakides and Nerode [MN1] (see for example, [Do2], [Gu], [KR], [Re1], [Re2], and [Sh]). For those unfamiliar with the literature on 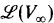 , we shall give a list of basic definitions required for this paper in §0.
, we shall give a list of basic definitions required for this paper in §0.
It is well known that complements in V∞ are not unique. For example, in [Re2] Remmel constructed r.e. spaces M1 and M2 and co-r.e. spaces Q1 and Q2 such that for all i, j ∈ {1, 2}, Mi ⊕ Qj = V∞ and M1 is supermaximal, M2 is not maximal, Q1 has a fully extendible basis, and Q2 has no extendible basis. We say a subspace Q of V∞ is fully co-r.e. if Q is generated by a co-r.e. subset of some recursive basis of V∞. Downey [Do2] has shown that every r.e. subspace of V∞ has a complement which is a fully co-r.e. subspace. Moreover suppose Q is any fully co-r.e. subspace, say Q = (C)* where C is a co-r.e. subset of a recursive basis B of V∞; if C is nonrecursive, then it is shown in [Do2] that Q has a decidable complement as well as a nondecidable nowhere simple complement.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 7
- Cited by


