Published online by Cambridge University Press: 12 March 2014
In this paper, by a function of ordinals we understand a function which is defined for all ordinals and each of whose value is an ordinal. In [7] (also cf. [8] or [9]) we defined recursive functions and predicates of ordinals, following Kleene's definition on natural numbers. A predicate will be called arithmetical, if it is obtained from a recursive predicate by prefixing a sequence of alternating quantifiers. A function will be called arithmetical, if its representing predicate is arithmetical.
The cardinals are identified with those ordinals a which have larger power than all smaller ordinals than a. For any given ordinal a, we denote by 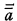 the cardinal of a and by 2a the cardinal which is of the same power as the power set of a. Let χ be the function such that χ(a) is the least cardinal which is greater than a.
the cardinal of a and by 2a the cardinal which is of the same power as the power set of a. Let χ be the function such that χ(a) is the least cardinal which is greater than a.
Now there are functions of ordinals such that they are easily defined in set theory, but it seems impossible to define them as arithmetical ones; χ is such a function. If we define χ in making use of only the language on ordinals, it seems necessary to use the notion of all the functions from ordinals, e.g., as in [6].