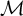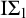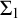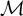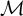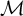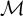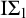1 Introduction
In 1973, Harvey Friedman proved a striking result for countable nonstandard models of finite set theory, and consequently for countable models of Peano arithmetic
![]() $ \mathrm {(PA)} $
stating that every countable nonstandard model of
$ \mathrm {(PA)} $
stating that every countable nonstandard model of
![]() $\mathrm {PA}$
carries a proper initial self-embedding; here an initial self-embedding is a self-embedding whose image is an initial segment of the ground model [Reference Friedman, Mathias and Rogers5]. Afterward, many versions of Friedman’s style theorem appeared in the literature of model theory of arithmetic (e.g., see [Reference Dimitracopoulos and Paris3] or [Reference Wilkie, Lachlan, Srebrny and Zarach16]). In [Reference Bahrami and Enayat1], it is shown that some results on the set of fixed points of automorphism of countable recursively saturated models of
$\mathrm {PA}$
carries a proper initial self-embedding; here an initial self-embedding is a self-embedding whose image is an initial segment of the ground model [Reference Friedman, Mathias and Rogers5]. Afterward, many versions of Friedman’s style theorem appeared in the literature of model theory of arithmetic (e.g., see [Reference Dimitracopoulos and Paris3] or [Reference Wilkie, Lachlan, Srebrny and Zarach16]). In [Reference Bahrami and Enayat1], it is shown that some results on the set of fixed points of automorphism of countable recursively saturated models of
![]() $\mathrm {PA}$
can be generalized for initial self-embeddings of countable nonstandard models of
$\mathrm {PA}$
can be generalized for initial self-embeddings of countable nonstandard models of
![]() $ \mathrm {I}\Sigma _{1} $
(see Theorem 2.4). In this paper, inspired by results about automorphisms of models of
$ \mathrm {I}\Sigma _{1} $
(see Theorem 2.4). In this paper, inspired by results about automorphisms of models of
![]() $\mathrm {PA}$
, we will investigate some more properties of countable models of
$\mathrm {PA}$
, we will investigate some more properties of countable models of
![]() $ \mathrm {I}\Sigma _{1} $
through initial self-embeddings.
$ \mathrm {I}\Sigma _{1} $
through initial self-embeddings.
In [Reference Enayat4], Enayat generalized the notion of a small submodel from [Reference Lascar, Kaye and Macpherson14], to I-small
Footnote
1
for a given cut I of a model of
![]() $\mathrm {PA}$
(see Definition 1), and proved that:
$\mathrm {PA}$
(see Definition 1), and proved that:
Theorem 1.1 (Enayat).
Suppose
![]() $ \mathcal {M}\models \mathrm {PA} $
is countable, recursively saturated, and I is a strong cut of
$ \mathcal {M}\models \mathrm {PA} $
is countable, recursively saturated, and I is a strong cut of
![]() $\mathcal {M}$
. Moreover, let
$\mathcal {M}$
. Moreover, let
![]() $ \mathcal {M}_{0}$
be an
$ \mathcal {M}_{0}$
be an
![]() $ I$
-small elementary submodel of
$ I$
-small elementary submodel of
![]() $\mathcal {M}$
. Then there exists some automorphism
$\mathcal {M}$
. Then there exists some automorphism
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ M_{0} $
is equal to the set of fixed points of
$ M_{0} $
is equal to the set of fixed points of
![]() $ j $
.
$ j $
.
In Section 3 of this paper, after investigating some basic properties of
![]() $ I$
-small
$ I$
-small
![]() $ \Sigma _{1}$
-elementary submodels of a countable model
$ \Sigma _{1}$
-elementary submodels of a countable model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
for some cut I of
$ \mathrm {I}\Sigma _{1} $
for some cut I of
![]() $\mathcal {M}$
, we will refine the above theorem for initial self-embeddings; i.e., we will show that I is strong in
$\mathcal {M}$
, we will refine the above theorem for initial self-embeddings; i.e., we will show that I is strong in
![]() $\mathcal {M}$
iff every
$\mathcal {M}$
iff every
![]() $ I$
-small
$ I$
-small
![]() $ \Sigma _{1}$
-elementary submodel of
$ \Sigma _{1}$
-elementary submodel of
![]() $\mathcal {M}$
is equal to the set of fixed points of some proper initial self-embedding of
$\mathcal {M}$
is equal to the set of fixed points of some proper initial self-embedding of
![]() $\mathcal {M}$
. This result also generalizes one of the main theorems of [Reference Bahrami and Enayat1] (see Corollary 4.3).
$\mathcal {M}$
. This result also generalizes one of the main theorems of [Reference Bahrami and Enayat1] (see Corollary 4.3).
Section 4 of this paper is devoted to the investigation of equivalent conditions to strongness of the standard cut, denoted by
![]() $ \mathbb {N} $
, in a countable model of
$ \mathbb {N} $
, in a countable model of
![]() $ \mathrm {I}\Sigma _{1} $
, through the set of fixed points of initial self-embeddings. In [Reference Kossak and Schmerl12], it is shown that:
$ \mathrm {I}\Sigma _{1} $
, through the set of fixed points of initial self-embeddings. In [Reference Kossak and Schmerl12], it is shown that:
Theorem 1.2 (Kossak–Schmerl).
Suppose
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() $\mathrm {PA}$
. If
$\mathrm {PA}$
. If
![]() $ \mathbb {N} $
is not strong in
$ \mathbb {N} $
is not strong in
![]() $\mathcal {M}$
, then for every automorphism
$\mathcal {M}$
, then for every automorphism
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
the set of fixed points of
$\mathcal {M}$
the set of fixed points of
![]() $ j $
is isomorphic to
$ j $
is isomorphic to
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
In Corollary 4.2, we will show that for every countable nonstandard model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
, if
$ \mathrm {I}\Sigma _{1} $
, if
![]() $ \mathbb {N} $
is not strong in
$ \mathbb {N} $
is not strong in
![]() $ \mathcal {M}$
, then the set of fixed points of any initial self-embedding
$ \mathcal {M}$
, then the set of fixed points of any initial self-embedding
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
is either a model of
$\mathcal {M}$
is either a model of
![]() $ \neg \mathrm {B}\Sigma _{1} $
, or is isomorphic to some proper initial segment of
$ \neg \mathrm {B}\Sigma _{1} $
, or is isomorphic to some proper initial segment of
![]() $\mathcal {M}$
. Then, we conclude that
$\mathcal {M}$
. Then, we conclude that
![]() $ \mathbb {N} $
is strong in a countable recursively saturated model
$ \mathbb {N} $
is strong in a countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathrm {PA}$
iff there exists some proper initial self-embedding
$\mathrm {PA}$
iff there exists some proper initial self-embedding
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
such that the set of fixed points of
$\mathcal {M}$
such that the set of fixed points of
![]() $ j $
is small in
$ j $
is small in
![]() $\mathcal {M}$
and consequently it is not isomorphic to any proper initial segment of
$\mathcal {M}$
and consequently it is not isomorphic to any proper initial segment of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
In Section 5, we will study the extendability of initial embeddings of models of
![]() $ \mathrm {I}\Sigma _{1} $
to larger models. In particular, we will prove that any isomorphism between two
$ \mathrm {I}\Sigma _{1} $
to larger models. In particular, we will prove that any isomorphism between two
![]() $ \Sigma _{1}$
-elementary initial segment of a countable nonstandard model
$ \Sigma _{1}$
-elementary initial segment of a countable nonstandard model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
is extendable to some initial self-embedding of
$ \mathrm {I}\Sigma _{1} $
is extendable to some initial self-embedding of
![]() $\mathcal {M}$
iff it preserves coded subsets (for the case of automorphisms of countable recursively saturated models of
$\mathcal {M}$
iff it preserves coded subsets (for the case of automorphisms of countable recursively saturated models of
![]() $\mathrm {PA}$
this condition is only a necessary condition for extendability to larger models [Reference Kossak and Kotlarski10]).
$\mathrm {PA}$
this condition is only a necessary condition for extendability to larger models [Reference Kossak and Kotlarski10]).
2 Preliminaries
In this section we will review some definitions and results which are used through this paper. All unexplained notions can be found in [Reference Hájek and Pudlák6, Reference Kaye7].
-
• Through this paper, we will work in the language of arithmetic
 $ {\mathcal {L}_{ A}:=\{+,.,<,0,1\}} $
. For a given class
$ {\mathcal {L}_{ A}:=\{+,.,<,0,1\}} $
. For a given class
 $ \Gamma $
of
$ \Gamma $
of
 $ \mathcal {L}$
-formulas (where
$ \mathcal {L}$
-formulas (where
 $ \mathcal {L}\supseteq \mathcal {L}_{ A} $
),
$ \mathcal {L}\supseteq \mathcal {L}_{ A} $
),
 $ \mathrm {I}\Gamma $
is the fragment of
$ \mathrm {I}\Gamma $
is the fragment of
 $\mathrm {PA}^{*}:=\mathrm {PA}(\mathcal {L})$
with the induction scheme limited to formulas of
$\mathrm {PA}^{*}:=\mathrm {PA}(\mathcal {L})$
with the induction scheme limited to formulas of
 $ \Gamma $
. The
$ \Gamma $
. The
 $\Gamma $
-Collection scheme, denoted by
$\Gamma $
-Collection scheme, denoted by
 $ \mathrm {B}\Gamma $
, consists of the formulas of the following form for every
$ \mathrm {B}\Gamma $
, consists of the formulas of the following form for every
 $\varphi \in \Gamma $
: Moreover, the strong
$\varphi \in \Gamma $
: Moreover, the strong $$ \begin{align*} \forall \bar{z},u \ ((\forall x<u \ \exists y \ \varphi(x,y,\bar{z}))\rightarrow \exists v \ (\forall x<u \ \exists y<v \ \varphi(x,y,\bar{z})) ). \end{align*} $$
$$ \begin{align*} \forall \bar{z},u \ ((\forall x<u \ \exists y \ \varphi(x,y,\bar{z}))\rightarrow \exists v \ (\forall x<u \ \exists y<v \ \varphi(x,y,\bar{z})) ). \end{align*} $$
 $\Gamma $
-Collection scheme, denoted by
$\Gamma $
-Collection scheme, denoted by
 $ \mathrm {B}^{+}\Gamma $
, consists of the formulas of the following form for every
$ \mathrm {B}^{+}\Gamma $
, consists of the formulas of the following form for every
 $\varphi \in \Gamma $
: It is folklore that
$\varphi \in \Gamma $
: It is folklore that $$ \begin{align*} \forall \bar{z},u \ \exists v \ \forall x<u \ (\exists y \ \varphi(x,y,\bar{z})\rightarrow \exists y<v \ \varphi(x,y,\bar{z})). \end{align*} $$
$$ \begin{align*} \forall \bar{z},u \ \exists v \ \forall x<u \ (\exists y \ \varphi(x,y,\bar{z})\rightarrow \exists y<v \ \varphi(x,y,\bar{z})). \end{align*} $$
 $ \mathrm {I}\Sigma _{n+1}\vdash \mathrm {B}^{+}\Sigma _{n+1}\vdash \mathrm {B}\Sigma _{n+1} $
for all
$ \mathrm {I}\Sigma _{n+1}\vdash \mathrm {B}^{+}\Sigma _{n+1}\vdash \mathrm {B}\Sigma _{n+1} $
for all
 $ n\in \omega $
; moreover, for every
$ n\in \omega $
; moreover, for every
 $ n\in \omega $
,
$ n\in \omega $
,
 $ \mathrm {I}\Sigma _{n}\nvdash \mathrm {B}\Sigma _{n+1} $
and
$ \mathrm {I}\Sigma _{n}\nvdash \mathrm {B}\Sigma _{n+1} $
and
 $ \mathrm {I}\Sigma _{n}\nvdash \neg \mathrm {B}\Sigma _{n+1} $
(see [Reference Hájek and Pudlák6, Chapter I]).
$ \mathrm {I}\Sigma _{n}\nvdash \neg \mathrm {B}\Sigma _{n+1} $
(see [Reference Hájek and Pudlák6, Chapter I]).
-
• Within
 $ \mathrm {I}\Delta _{0}+\mathrm {Exp}$
, the
$ \mathrm {I}\Delta _{0}+\mathrm {Exp}$
, the
 $ \Delta _{0}$
-formula
$ \Delta _{0}$
-formula
 $ x\mathrm {E} y $
denotes the Ackermann’s membership relation, asserting that “the x-th bit of the binary expansion of y is 1.” For every
$ x\mathrm {E} y $
denotes the Ackermann’s membership relation, asserting that “the x-th bit of the binary expansion of y is 1.” For every
 ${\mathcal {M}\models \mathrm {I}\Delta _{0}+\mathrm {Exp}} $
and each
${\mathcal {M}\models \mathrm {I}\Delta _{0}+\mathrm {Exp}} $
and each
 $ a\in M $
,
$ a\in M $
,
 $ a_{\mathrm {E}} $
denotes the set of
$ a_{\mathrm {E}} $
denotes the set of
 $ \mathrm {E}$
-members of
$ \mathrm {E}$
-members of
 $ a $
in
$ a $
in
 $\mathcal {M}$
. Moreover, the
$\mathcal {M}$
. Moreover, the
 $ \Delta _{0}$
-formulas
$ \Delta _{0}$
-formulas
 $ \mathrm {Card}(x)=y $
,
$ \mathrm {Card}(x)=y $
,
 $ \langle \bar {x}\rangle =y $
,
$ \langle \bar {x}\rangle =y $
,
 $ \mathrm {Len}(x)=y $
,
$ \mathrm {Len}(x)=y $
,
 $ (x)_{y}=z $
, and
$ (x)_{y}=z $
, and
 $ x\upharpoonright _{y}=z, $
respectively, express that “there exists some bijection between y and the set coded by
$ x\upharpoonright _{y}=z, $
respectively, express that “there exists some bijection between y and the set coded by
 $x,$
” “the sequence number of
$x,$
” “the sequence number of
 $\bar {x}$
is y,” “length of the sequence coded by x is
$\bar {x}$
is y,” “length of the sequence coded by x is
 $y,$
” “the yth element of the sequence number x is z,” and “the restriction of the sequence number x to y is z.” In addition, for every formula
$y,$
” “the yth element of the sequence number x is z,” and “the restriction of the sequence number x to y is z.” In addition, for every formula
 $ \varphi (x) $
, by the formula
$ \varphi (x) $
, by the formula
 $ y=\mu _{x}\ \varphi (x) $
we mean “y is the least element such that
$ y=\mu _{x}\ \varphi (x) $
we mean “y is the least element such that
 $\varphi (y)$
holds.”
$\varphi (y)$
holds.”Furthermore, for every
 $ n\in \omega $
there exist
$ n\in \omega $
there exist
 $ \mathcal {L}_{ A}$
-formulas
$ \mathcal {L}_{ A}$
-formulas
 $ \mathrm {Sat}_{\Sigma _{n}} $
and
$ \mathrm {Sat}_{\Sigma _{n}} $
and
 $ \mathrm {Sat}_{\Pi _{n}} $
which define the satisfaction predicate for
$ \mathrm {Sat}_{\Pi _{n}} $
which define the satisfaction predicate for
 $\Sigma _{n}$
-formulas and
$\Sigma _{n}$
-formulas and
 $ \Pi _{n}$
-formulas, respectively, in an ambient model. For every natural number
$ \Pi _{n}$
-formulas, respectively, in an ambient model. For every natural number
 $ n>0 $
, it can be shown that
$ n>0 $
, it can be shown that
 $ \mathrm {Sat}_{\Sigma _{n}} $
and
$ \mathrm {Sat}_{\Sigma _{n}} $
and
 $ \mathrm {Sat}_{\Pi _{n}} $
are
$ \mathrm {Sat}_{\Pi _{n}} $
are
 $ \Sigma _{n} $
and
$ \Sigma _{n} $
and
 $ \Pi _{n,} $
respectively, in
$ \Pi _{n,} $
respectively, in
 $ \mathrm {I}\Sigma _{1} $
. Moreover,
$ \mathrm {I}\Sigma _{1} $
. Moreover,
 $ \mathrm {Sat}_{\Delta _{0}}\in \Delta _{1}^{\mathrm {I}\Sigma _{1}} $
[Reference Hájek and Pudlák6, Chapter I, Theorem 1.75]. If
$ \mathrm {Sat}_{\Delta _{0}}\in \Delta _{1}^{\mathrm {I}\Sigma _{1}} $
[Reference Hájek and Pudlák6, Chapter I, Theorem 1.75]. If
 $\mathcal {M}$
is a nonstandard model of
$\mathcal {M}$
is a nonstandard model of
 $ \mathrm {I}\Sigma _{n} $
, the aforementioned feature along with
$ \mathrm {I}\Sigma _{n} $
, the aforementioned feature along with
 $ \Sigma _{n}$
-Overspill in
$ \Sigma _{n}$
-Overspill in
 $\mathcal {M}$
imply that every coded
$\mathcal {M}$
imply that every coded
 $ \Sigma _{n}$
-type and every coded bounded
$ \Sigma _{n}$
-type and every coded bounded
 $ \Pi _{n}$
-type is realized in
$ \Pi _{n}$
-type is realized in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
•
 $ \Sigma _{n}$
-Pigeonhole Principle. For every
$ \Sigma _{n}$
-Pigeonhole Principle. For every
 $n>0$
, if
$n>0$
, if
 $ \mathcal {M}\models \mathrm {I}\Sigma _{n}$
,
$ \mathcal {M}\models \mathrm {I}\Sigma _{n}$
,
 $a\in M $
, and
$a\in M $
, and
 $\varphi $
is a
$\varphi $
is a
 $ \Sigma _{1}$
-formula which defines a function from
$ \Sigma _{1}$
-formula which defines a function from
 $ a+1 $
into a in
$ a+1 $
into a in
 $\mathcal {M}$
, then
$\mathcal {M}$
, then
 $ \varphi $
is not one-to-one [Reference Hájek and Pudlák6].
$ \varphi $
is not one-to-one [Reference Hájek and Pudlák6]. -
• Given
 $ \mathcal {L}_{A}$
-structure
$ \mathcal {L}_{A}$
-structure
 $\mathcal {M}$
and subset X of M, for every
$\mathcal {M}$
and subset X of M, for every
 $n>0$
, we define:
$n>0$
, we define:-
–
 $ \mathrm {K}^{n}(\mathcal {M};X):=$
the set of all
$ \mathrm {K}^{n}(\mathcal {M};X):=$
the set of all
 $\Sigma _{n}$
-definable element of
$\Sigma _{n}$
-definable element of
 $\mathcal {M}$
with parameters from
$\mathcal {M}$
with parameters from
 $ X $
.
$ X $
. -
–
 $ \mathrm {I}^{n}(\mathcal {M};X):=\{x: \ x\leq a \text { for some } a\in \mathrm {K}^{n}(\mathcal {M};X)\} $
.
$ \mathrm {I}^{n}(\mathcal {M};X):=\{x: \ x\leq a \text { for some } a\in \mathrm {K}^{n}(\mathcal {M};X)\} $
. -
–
 $ \mathrm {H}^{n}(\mathcal {M};X):=\bigcup _{k\in \omega }\mathrm {H}_{k}^{n}(\mathcal {M};X) $
, where:
$ \mathrm {H}^{n}(\mathcal {M};X):=\bigcup _{k\in \omega }\mathrm {H}_{k}^{n}(\mathcal {M};X) $
, where:  $$ \begin{align*} &\quad \mathrm{H}_{0}^{n}(\mathcal{M};X):=\mathrm{I}^{n}(\mathcal{M};X), \text{ and } \\ &\mathrm{H}_{k+1}^{n}(\mathcal{M};X):=\mathrm{I}^{n}(\mathcal{M};\mathrm{H}_{k}^{n}(\mathcal{M};X)). \end{align*} $$
$$ \begin{align*} &\quad \mathrm{H}_{0}^{n}(\mathcal{M};X):=\mathrm{I}^{n}(\mathcal{M};X), \text{ and } \\ &\mathrm{H}_{k+1}^{n}(\mathcal{M};X):=\mathrm{I}^{n}(\mathcal{M};\mathrm{H}_{k}^{n}(\mathcal{M};X)). \end{align*} $$
-
–
 ${\mathrm {K}(\mathcal {M};X):=\cup _{n\in \omega }\mathrm {K}^{n}(\mathcal {M};X)}$
.
${\mathrm {K}(\mathcal {M};X):=\cup _{n\in \omega }\mathrm {K}^{n}(\mathcal {M};X)}$
.
(When
 $ X=\emptyset $
, we omit
$ X=\emptyset $
, we omit
 $ X $
from the notations.) Clearly,
$ X $
from the notations.) Clearly,
 $\mathrm {I}^{n}(\mathcal {M};X) $
and
$\mathrm {I}^{n}(\mathcal {M};X) $
and
 $ \mathrm {H}^{n}(\mathcal {M};X) $
are initial segments of
$ \mathrm {H}^{n}(\mathcal {M};X) $
are initial segments of
 $\mathcal {M}$
. The following properties of these submodels of
$\mathcal {M}$
. The following properties of these submodels of
 $\mathcal {M}$
are well-known (see, e.g., [Reference Hájek and Pudlák6, Chapter IV, Theorem 1.33]):
$\mathcal {M}$
are well-known (see, e.g., [Reference Hájek and Pudlák6, Chapter IV, Theorem 1.33]):Theorem 2.1. Suppose
 $ n>0 $
, and
$ n>0 $
, and
 $ \mathcal {M}\models \mathrm {I}\Sigma _{n} $
and
$ \mathcal {M}\models \mathrm {I}\Sigma _{n} $
and
 $ X\subseteq M $
, then the following hold:
$ X\subseteq M $
, then the following hold: -
(1)
 $\mathrm {K}^{n}(\mathcal {M};X)\prec _{\Sigma _{n}}\mathcal {M} $
, and if
$\mathrm {K}^{n}(\mathcal {M};X)\prec _{\Sigma _{n}}\mathcal {M} $
, and if
 $ \mathrm {K}^{n}(\mathcal {M}) $
is nonstandard, then
$ \mathrm {K}^{n}(\mathcal {M}) $
is nonstandard, then
 $\mathrm {K}^{n}(\mathcal {M})\models \neg \mathrm {B}\Sigma _{n} $
.
$\mathrm {K}^{n}(\mathcal {M})\models \neg \mathrm {B}\Sigma _{n} $
. -
(2)
 $\mathrm {I}^{n}(\mathcal {M};X)\prec _{\Sigma _{n-1}}\mathcal {M} $
and
$\mathrm {I}^{n}(\mathcal {M};X)\prec _{\Sigma _{n-1}}\mathcal {M} $
and
 $\mathrm {I}^{n}(\mathcal {M};X)\models \mathrm {B}\Sigma _{n} $
.
$\mathrm {I}^{n}(\mathcal {M};X)\models \mathrm {B}\Sigma _{n} $
. -
(3)
 $\mathrm {H}^{n}(\mathcal {M};X)\prec _{\Sigma _{n}}\mathcal {M} $
and
$\mathrm {H}^{n}(\mathcal {M};X)\prec _{\Sigma _{n}}\mathcal {M} $
and
 $\mathrm {H}^{n}(\mathcal {M};X)\models \mathrm {B}\Sigma _{n+1} $
.
$\mathrm {H}^{n}(\mathcal {M};X)\models \mathrm {B}\Sigma _{n+1} $
.
-
-
• A given structure
 $\mathcal {M}$
is called recursively saturated if it realizes every recursive type with finite number of parameters in
$\mathcal {M}$
is called recursively saturated if it realizes every recursive type with finite number of parameters in
 $ M $
. In [Reference Barwise, Schlipf, Saracino and Weispfenning2], Barwise and Shilipf showed that any countable model
$ M $
. In [Reference Barwise, Schlipf, Saracino and Weispfenning2], Barwise and Shilipf showed that any countable model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $\mathrm {PA}$
is recursively saturated iff it carries an inductive satisfaction class; here an inductive satisfaction class
$\mathrm {PA}$
is recursively saturated iff it carries an inductive satisfaction class; here an inductive satisfaction class
 $ S $
of
$ S $
of
 $\mathcal {M}$
is a subset of
$\mathcal {M}$
is a subset of
 $ M $
which contains
$ M $
which contains
 $ \langle \varphi ,a\rangle $
such that (1)
$ \langle \varphi ,a\rangle $
such that (1)
 $ \mathcal {M}\models \mathrm {Form}(\varphi ) $
, (2)
$ \mathcal {M}\models \mathrm {Form}(\varphi ) $
, (2)
 $ (\mathcal {M}; S)\models \mathrm {PA}^{*} $
, and (3)
$ (\mathcal {M}; S)\models \mathrm {PA}^{*} $
, and (3)
 $ (\mathcal {M}; S) $
satisfies Tarski’s inductive conditions for satisfaction (for a more precise definition see [Reference Kaye7]). Smoryński in [Reference Smoryński15], by generalizing Barwise–Ressayre expandability result, proved that for every countable recursively saturated model
$ (\mathcal {M}; S) $
satisfies Tarski’s inductive conditions for satisfaction (for a more precise definition see [Reference Kaye7]). Smoryński in [Reference Smoryński15], by generalizing Barwise–Ressayre expandability result, proved that for every countable recursively saturated model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $\mathrm {PA}$
there exists some inductive satisfaction class S such that
$\mathrm {PA}$
there exists some inductive satisfaction class S such that
 $(\mathcal {M}; S)$
is also recursively saturated.
$(\mathcal {M}; S)$
is also recursively saturated. -
• For every cut I of
 $\mathcal {M}$
the I-Standard System of
$\mathcal {M}$
the I-Standard System of
 $\mathcal {M}$
, denoted by
$\mathcal {M}$
, denoted by
 $ \mathrm {SSy}_{I}(\mathcal {M}) $
, is the family of subsets of I of the form
$ \mathrm {SSy}_{I}(\mathcal {M}) $
, is the family of subsets of I of the form
 $ I\cap a_{\mathrm {E}} $
for some
$ I\cap a_{\mathrm {E}} $
for some
 $ a\in M $
. By
$ a\in M $
. By
 $ \mathrm {SSy}(\mathcal {M}) $
we mean
$ \mathrm {SSy}(\mathcal {M}) $
we mean
 $ \mathrm {SSy}_{\mathbb {N}}(\mathcal {M}) $
. It is well-known that for every model
$ \mathrm {SSy}_{\mathbb {N}}(\mathcal {M}) $
. It is well-known that for every model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $ \mathrm {I}\Sigma _{n} $
(for
$ \mathrm {I}\Sigma _{n} $
(for
 $ n>0 $
),
$ n>0 $
),
 $ \mathrm {SSy}_{I}(\mathcal {M}) $
is equal to the family of intersections of
$ \mathrm {SSy}_{I}(\mathcal {M}) $
is equal to the family of intersections of
 $ \Sigma _{n}$
-definable (with parameters) subsets of
$ \Sigma _{n}$
-definable (with parameters) subsets of
 $\mathcal {M}$
with I (see [Reference Hájek and Pudlák6, Chapter I]). Moreover, it is easy to check that if
$\mathcal {M}$
with I (see [Reference Hájek and Pudlák6, Chapter I]). Moreover, it is easy to check that if
 $ \mathcal {N}$
is an initial segment and a submodel of
$ \mathcal {N}$
is an initial segment and a submodel of
 $\mathcal {M}$
containing I, then
$\mathcal {M}$
containing I, then
 $\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N}) $
(see [Reference Kaye7]).
$\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N}) $
(see [Reference Kaye7]). -
• A given model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $ \mathrm {I}\Delta _{0} $
is called 1-tall if
$ \mathrm {I}\Delta _{0} $
is called 1-tall if
 $ \mathrm {K}^{1}(\mathcal {M};a) $
is cofinal in
$ \mathrm {K}^{1}(\mathcal {M};a) $
is cofinal in
 $\mathcal {M}$
for no
$\mathcal {M}$
for no
 $ a\in M $
; and it is called 1-extendable if it possesses some end extension
$ a\in M $
; and it is called 1-extendable if it possesses some end extension
 $ \mathcal {N}\models \mathrm {I}\Delta _{0} $
such that
$ \mathcal {N}\models \mathrm {I}\Delta _{0} $
such that
 $ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})=\mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
. Dimitracopoulos and Paris [Reference Dimitracopoulos and Paris3] showed that:
$ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})=\mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
. Dimitracopoulos and Paris [Reference Dimitracopoulos and Paris3] showed that:Theorem 2.2 (Dimitracopoulos–Paris).
-
(1) For any two countable and nonstandard models
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ \mathcal {N} $
of
$ \mathcal {N} $
of
 $ \mathrm {I}\Delta _{0}+\mathrm {Exp} $
such that
$ \mathrm {I}\Delta _{0}+\mathrm {Exp} $
such that
 $\mathcal {M}$
is 1-extendable and
$\mathcal {M}$
is 1-extendable and
 $ \mathcal {N} $
is 1-tall, there exists a proper initial embedding from
$ \mathcal {N} $
is 1-tall, there exists a proper initial embedding from
 $\mathcal {M}$
into
$\mathcal {M}$
into
 $ \mathcal {N} $
iff
$ \mathcal {N} $
iff
 $ \mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}) $
and
$ \mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}) $
and
 $ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
.
$ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
. -
(2) Any 1-tall countable model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $ \mathrm {B}\Sigma _{1}+\mathrm {Exp} $
in which
$ \mathrm {B}\Sigma _{1}+\mathrm {Exp} $
in which
 $ \mathbb {N} $
is not
$ \mathbb {N} $
is not
 $ \Pi _{1} $
-definable (without parameters), is 1-extendable.
$ \Pi _{1} $
-definable (without parameters), is 1-extendable.
-
-
• A cut I of a model
 $\mathcal {M}$
is called strong if for every coded function
$\mathcal {M}$
is called strong if for every coded function
 $ f $
of
$ f $
of
 $\mathcal {M}$
whose domain contains I, there exists some
$\mathcal {M}$
whose domain contains I, there exists some
 $ e>I $
such that
$ e>I $
such that
 $ f(i)\in I $
iff
$ f(i)\in I $
iff
 $ f(i)<e $
for all
$ f(i)<e $
for all
 $ i\in I $
. Paris and Kirby, in [Reference Kirby and Paris9], proved that I is a strong cut of a model
$ i\in I $
. Paris and Kirby, in [Reference Kirby and Paris9], proved that I is a strong cut of a model
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $ \mathrm {I}\Delta _{0}+\mathrm {Exp}$
iff
$ \mathrm {I}\Delta _{0}+\mathrm {Exp}$
iff
 $ (I,\mathrm {SSy}_{I}(\mathcal {M}))\models \mathrm {ACA}_{0} $
(here
$ (I,\mathrm {SSy}_{I}(\mathcal {M}))\models \mathrm {ACA}_{0} $
(here
 $ \mathrm {ACA}_{0} $
is the subsystem of second order arithmetic with the comprehension scheme restricted to formulas with no second order quantifiers).
$ \mathrm {ACA}_{0} $
is the subsystem of second order arithmetic with the comprehension scheme restricted to formulas with no second order quantifiers). -
• For given
 $ \mathcal {L}_{A}$
-structures
$ \mathcal {L}_{A}$
-structures
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ \mathcal {N} $
, an (a proper) initial embedding j is an embedding from
$ \mathcal {N} $
, an (a proper) initial embedding j is an embedding from
 $\mathcal {M}$
into
$\mathcal {M}$
into
 $ \mathcal {N} $
whose image is an (a proper) initial segment of
$ \mathcal {N} $
whose image is an (a proper) initial segment of
 $ \mathcal {N} $
. To every self-embedding
$ \mathcal {N} $
. To every self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
, we associate two subsets of M: In [Reference Bahrami and Enayat1], it is shown that for every model
$\mathcal {M}$
, we associate two subsets of M: In [Reference Bahrami and Enayat1], it is shown that for every model $$ \begin{align*} &\mathrm{I}_{\mathrm{fix}}(j):=\{m\in M:\forall x\leq m\ j(x)=x\}, \text{ and} \\ &\qquad \mathrm{Fix}(j):=\{m\in M:j(m)=m\}. \end{align*} $$
$$ \begin{align*} &\mathrm{I}_{\mathrm{fix}}(j):=\{m\in M:\forall x\leq m\ j(x)=x\}, \text{ and} \\ &\qquad \mathrm{Fix}(j):=\{m\in M:j(m)=m\}. \end{align*} $$
 $\mathcal {M}$
of
$\mathcal {M}$
of
 $ \mathrm {I}\Sigma _{1} $
, and any self-embedding
$ \mathrm {I}\Sigma _{1} $
, and any self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
, it holds that
$\mathcal {M}$
, it holds that
 $K^{1}(\mathcal {M})\prec _{\Sigma _{1}} \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M}$
. Consequently,
$K^{1}(\mathcal {M})\prec _{\Sigma _{1}} \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M}$
. Consequently,
 $ \mathrm {Fix}(j)\models \mathrm {I}\Delta _{0}+\mathrm {Exp}. $
The following results on the set of fixed points of initial self-embeddings were also proved in [Reference Bahrami and Enayat1]:
$ \mathrm {Fix}(j)\models \mathrm {I}\Delta _{0}+\mathrm {Exp}. $
The following results on the set of fixed points of initial self-embeddings were also proved in [Reference Bahrami and Enayat1]:Theorem 2.3 (B-Enayat).
Let
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ \mathcal {N} $
be countable nonstandard models of
$ \mathcal {N} $
be countable nonstandard models of
 $ \mathrm {I}\Sigma _{1} $
,
$ \mathrm {I}\Sigma _{1} $
,
 $ c\in M $
and
$ c\in M $
and
 $d,b\in N $
, and let I be a proper cut shared by
$d,b\in N $
, and let I be a proper cut shared by
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ \mathcal {N} $
which is closed under exponentiation. Then the following are equivalent:
$ \mathcal {N} $
which is closed under exponentiation. Then the following are equivalent: -
(1) There exists some proper initial embedding
 $ j $
from
$ j $
from
 $\mathcal {M}$
into
$\mathcal {M}$
into
 $ \mathcal {N} $
such that
$ \mathcal {N} $
such that
 $ I\subseteq \mathrm {I}_{\mathrm {fix}}(j) $
,
$ I\subseteq \mathrm {I}_{\mathrm {fix}}(j) $
,
 $ j(M)<b $
, and
$ j(M)<b $
, and
 $ j(c)=d $
.
$ j(c)=d $
. -
(2)
 $ \mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N}) $
, and for every
$ \mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N}) $
, and for every
 $ \Delta _{0}$
-formula
$ \Delta _{0}$
-formula
 $ \delta (z,x,y) $
and every
$ \delta (z,x,y) $
and every
 $ i\in I $
it holds that
$ i\in I $
it holds that  $$ \begin{align*}\mathcal{M}\models\exists z \ \delta(z,c,i) \ \Rightarrow \ \mathcal{N}\models\exists z<b \ \delta(z,d,i) .\end{align*} $$
$$ \begin{align*}\mathcal{M}\models\exists z \ \delta(z,c,i) \ \Rightarrow \ \mathcal{N}\models\exists z<b \ \delta(z,d,i) .\end{align*} $$
Remark 1. With the above assumptions, suppose
 $ a\in M\cap N $
such that for all
$ a\in M\cap N $
such that for all
 $ \Delta _{0}$
-formula
$ \Delta _{0}$
-formula
 $ \delta $
and for every
$ \delta $
and for every
 $ i\in I $
it holds that
$ i\in I $
it holds that  $$ \begin{align*} \mathcal{M}\models\exists z \ \delta(z,c,(a)_{i}) \ \Rightarrow \ \mathcal{N}\models\exists z<b \ \delta(z,d,(a)_{i}). \end{align*} $$
$$ \begin{align*} \mathcal{M}\models\exists z \ \delta(z,c,(a)_{i}) \ \Rightarrow \ \mathcal{N}\models\exists z<b \ \delta(z,d,(a)_{i}). \end{align*} $$
Then, by an appropriate modification in the proof of Theorem 2.3, we can manage to construct the above proper initial embedding j with the additional feature that
 $ {j((a)_{i})=(a)_{i}} $
for every
$ {j((a)_{i})=(a)_{i}} $
for every
 $ i\in I $
.
$ i\in I $
.Theorem 2.4 (B-Enayat).
Suppose
 $\mathcal {M}\models \mathrm {I}\Sigma _{1}$
is countable and nonstandard and I is a cut of
$\mathcal {M}\models \mathrm {I}\Sigma _{1}$
is countable and nonstandard and I is a cut of
 $\mathcal {M}$
. Then the following hold:
$\mathcal {M}$
. Then the following hold: -
(1) I is closed under exponentiation iff there exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {I}_{\mathrm {fix}}(j)=I $
.
$ \mathrm {I}_{\mathrm {fix}}(j)=I $
. -
(2) I is strong in
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ I\prec _{\Sigma _{1}}\mathcal {M} $
, iff there exists some proper initial self-embedding
$ I\prec _{\Sigma _{1}}\mathcal {M} $
, iff there exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)=I $
.
$ \mathrm {Fix}(j)=I $
. -
(3)
 $ \mathbb {N} $
is strong in
$ \mathbb {N} $
is strong in
 $\mathcal {M}$
iff there exists some proper initial self-embedding
$\mathcal {M}$
iff there exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)=\mathrm {K}^{1}(\mathcal {M}) $
.
$ \mathrm {Fix}(j)=\mathrm {K}^{1}(\mathcal {M}) $
.
The following lemma from [Reference Bahrami and Enayat1] will be useful in Section 4 of this paper:
Lemma 2.5. Suppose
 $ \mathcal {M}\models \mathrm {I}\Delta _{0}+\mathrm {Exp} $
in which
$ \mathcal {M}\models \mathrm {I}\Delta _{0}+\mathrm {Exp} $
in which
 $\mathbb {N}$
is not a strong cut, then for any self-embedding j of
$\mathbb {N}$
is not a strong cut, then for any self-embedding j of
 $\mathcal {M}$
, the following hold:
$\mathcal {M}$
, the following hold: -
(1) The nonstandard fixed points of j are downward cofinal in the nonstandard part of
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(2) For every element
 $a\in M$
, and
$a\in M$
, and
 $ m\in \mathrm {Fix}(j) $
there exists an element
$ m\in \mathrm {Fix}(j) $
there exists an element
 $b\in \mathrm {Fix} (j)$
such that
$b\in \mathrm {Fix} (j)$
such that  $$ \begin{align*} \mathrm{Th}_{\Sigma _{1}}(\mathcal{M};a,m)\subseteq \mathrm{Th}_{\Sigma _{1}}(\mathcal{M};b,m). \end{align*} $$
$$ \begin{align*} \mathrm{Th}_{\Sigma _{1}}(\mathcal{M};a,m)\subseteq \mathrm{Th}_{\Sigma _{1}}(\mathcal{M};b,m). \end{align*} $$
Convention. Suppose
 $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
and
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
and
 $ \langle \delta _{r}: \ r\in M\rangle $
is a canonical enumeration of all
$ \langle \delta _{r}: \ r\in M\rangle $
is a canonical enumeration of all
 $ \Delta _{0}$
-formulas within
$ \Delta _{0}$
-formulas within
 $\mathcal {M}$
as in [Reference Hájek and Pudlák6, Chapter I]. To be more precise,
$\mathcal {M}$
as in [Reference Hájek and Pudlák6, Chapter I]. To be more precise,
 $ \langle \delta _{r}: \ r\in M\rangle $
is an enumeration of all
$ \langle \delta _{r}: \ r\in M\rangle $
is an enumeration of all
 $ \Delta _{0} $
-formulas of
$ \Delta _{0} $
-formulas of
 $\mathcal {M}$
(containing nonstandard formulas) such that for every
$\mathcal {M}$
(containing nonstandard formulas) such that for every
 $ r\in M $
it holds that
$ r\in M $
it holds that-
•
 $ \delta _{r} $
is a standard
$ \delta _{r} $
is a standard
 $ \Delta _{0} $
-formula for all standard
$ \Delta _{0} $
-formula for all standard
 $ r\in M $
, and
$ r\in M $
, and -
• for every
 $ \Delta _{0} $
-formula
$ \Delta _{0} $
-formula
 $ \delta $
there exists some standard
$ \delta $
there exists some standard
 $ r\in M $
such that
$ r\in M $
such that
 $\mathcal {M}$
believes that
$\mathcal {M}$
believes that
 $ r $
is the Gödel number of
$ r $
is the Gödel number of
 $ \delta $
.
$ \delta $
.
(For more details see [Reference Hájek and Pudlák6] or [Reference Kaye7].)
Now, for every
 $ r\in M $
, we define the following notations:
$ r\in M $
, we define the following notations:-
•
 $ f_{r}(\diamondsuit )=\blacklozenge $
denotes the following partial
$ f_{r}(\diamondsuit )=\blacklozenge $
denotes the following partial
 $ \Sigma _{1}$
-function in
$ \Sigma _{1}$
-function in
 $\mathcal {M}$
:
$\mathcal {M}$
:  $$ \begin{align*} \exists z ((z)_{0}=\blacklozenge \ \wedge \ z=\mu_{y}\mathrm{Sat}_{\Delta_{0}}(\delta_{r}(\diamondsuit,(y)_{0},(y)_{1})). \end{align*} $$
$$ \begin{align*} \exists z ((z)_{0}=\blacklozenge \ \wedge \ z=\mu_{y}\mathrm{Sat}_{\Delta_{0}}(\delta_{r}(\diamondsuit,(y)_{0},(y)_{1})). \end{align*} $$
-
• The notation
 $ [f_{r}(\bar {x})\downarrow ] $
denotes the
$ [f_{r}(\bar {x})\downarrow ] $
denotes the
 $ \Sigma _{1}$
-formula
$ \Sigma _{1}$
-formula
 $ \exists z,y \ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(\bar {x},y,z)) $
, and
$ \exists z,y \ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(\bar {x},y,z)) $
, and
 ${ [f_{r}(\bar {x})\downarrow ]^{<w}} $
stands for the formula
${ [f_{r}(\bar {x})\downarrow ]^{<w}} $
stands for the formula
 $ \exists z,y<w \ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(\bar {x},y,z)) $
.
$ \exists z,y<w \ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(\bar {x},y,z)) $
. -
• Let
 $ \mathcal {F}(\mathcal {M}) $
to be the collection of all
$ \mathcal {F}(\mathcal {M}) $
to be the collection of all
 $ \emptyset $
-definable partial
$ \emptyset $
-definable partial
 $ \Sigma _{1}$
-functions in
$ \Sigma _{1}$
-functions in
 $\mathcal {M}$
.
$\mathcal {M}$
.
First note that, it is shown in [Reference Bahrami and Enayat1] that
Clearly, $$ \begin{align*} \mathrm{K}^{1}(\mathcal{M};a)=\{f(a): \ f\in\mathcal{F}(\mathcal{M}) \text{ and } \mathcal{M}\models[f(a)\downarrow] \}. \end{align*} $$
$$ \begin{align*} \mathrm{K}^{1}(\mathcal{M};a)=\{f(a): \ f\in\mathcal{F}(\mathcal{M}) \text{ and } \mathcal{M}\models[f(a)\downarrow] \}. \end{align*} $$
 $ f_{r}\in \mathcal {F}(\mathcal {M}) $
for all standard
$ f_{r}\in \mathcal {F}(\mathcal {M}) $
for all standard
 $ r\in M $
. Moreover, by a little bit of effort we can show that for every
$ r\in M $
. Moreover, by a little bit of effort we can show that for every
 $ f\in \mathcal {F}(\mathcal {M}) $
there exists some standard
$ f\in \mathcal {F}(\mathcal {M}) $
there exists some standard
 $ r\in M $
such that
$ r\in M $
such that
 $ f=f_{r}$
(for details see [Reference Bahrami and Enayat1, Lemma 3.1.2]).
$ f=f_{r}$
(for details see [Reference Bahrami and Enayat1, Lemma 3.1.2]).
As a result, if
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $ \mathcal {N} $
are two models of
$ \mathcal {N} $
are two models of
 $ \mathrm {I}\Delta _{0} $
such that
$ \mathrm {I}\Delta _{0} $
such that
 $ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})=\mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
, then
$ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M})=\mathrm {Th}_{\Sigma _{1}}(\mathcal {N}) $
, then
 $\mathcal {F}(\mathcal {M})=\mathcal {F}(\mathcal {N})= \mathcal {F}:=\{f_{n}: n\in \mathbb {N}\} $
.
$\mathcal {F}(\mathcal {M})=\mathcal {F}(\mathcal {N})= \mathcal {F}:=\{f_{n}: n\in \mathbb {N}\} $
. -
3
I-small
 $ \Sigma _{1}$
-elementary submodels
$ \Sigma _{1}$
-elementary submodels
In [Reference Lascar, Kaye and Macpherson14], Lascar introduced a class of submodels of models of arithmetic, namely small submodels, which resemble those submodels of a model of set theory whose cardinality is less than the cardinality of the ground model. Then, Enayat inspired by a result of Schmerl (stated without proof as Theorem 5.7 in [Reference Kaye, Kossak and Kotlarski8]), generalized this notion in [Reference Enayat4]. In this section we will prove some results about these submodels.
Definition 1. For a given proper cut I of a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Delta _{0}+\mathrm {Exp} $
, subset
$ \mathrm {I}\Delta _{0}+\mathrm {Exp} $
, subset
![]() $ X $
of
$ X $
of
![]() $ M $
is called I-small in
$ M $
is called I-small in
![]() $\mathcal {M}$
if there exists some
$\mathcal {M}$
if there exists some
![]() $ a\in M $
such that
$ a\in M $
such that
![]() $ X=\{(a)_{i} : \ i\in I\} $
, and
$ X=\{(a)_{i} : \ i\in I\} $
, and
![]() $ (a)_{i}\neq (a)_{j} $
for all distinct
$ (a)_{i}\neq (a)_{j} $
for all distinct
![]() $ i,j\in I $
. When
$ i,j\in I $
. When
![]() $ I=\mathbb {N} $
, we simply use small for
$ I=\mathbb {N} $
, we simply use small for
![]() $ \mathbb {N}$
-small.
$ \mathbb {N}$
-small.
It is easy to see that for every model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
, each proper cut I of
$ \mathrm {I}\Sigma _{1} $
, each proper cut I of
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $ I$
-small. Moreover, for every
$ I$
-small. Moreover, for every
![]() $ a\in M $
,
$ a\in M $
,
![]() $ \mathrm {K}^{1}(\mathcal {M};a) $
is small in
$ \mathrm {K}^{1}(\mathcal {M};a) $
is small in
![]() $\mathcal {M}$
. In [Reference Kossak and Schmerl12], it is shown that every recursively saturated model
$\mathcal {M}$
. In [Reference Kossak and Schmerl12], it is shown that every recursively saturated model
![]() $ \mathcal {M}$
of
$ \mathcal {M}$
of
![]() $\mathrm {PA} $
possesses some small submodel which is not finitely generated. This result can be generalized for
$\mathrm {PA} $
possesses some small submodel which is not finitely generated. This result can be generalized for
![]() $ I$
-small submodels, when I is a strong cut of
$ I$
-small submodels, when I is a strong cut of
![]() $\mathcal {M}$
(see Theorem 3.2). Furthermore, By using compactness arguments, for every model
$\mathcal {M}$
(see Theorem 3.2). Furthermore, By using compactness arguments, for every model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
, we can find some elementary extension of
$ \mathrm {I}\Sigma _{1} $
, we can find some elementary extension of
![]() $\mathcal {M}$
in which it is small. And finally, in [Reference Kossak and Kotlarski11] it is shown that every nonstandard small submodel is a mixed submodel (i.e., neither cofinal, nor initial segment). In a similar manner, for every cut I of a model
$\mathcal {M}$
in which it is small. And finally, in [Reference Kossak and Kotlarski11] it is shown that every nonstandard small submodel is a mixed submodel (i.e., neither cofinal, nor initial segment). In a similar manner, for every cut I of a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $ \mathrm {I}\Sigma _{1} $
, and each
$ \mathrm {I}\Sigma _{1} $
, and each
![]() $ I$
-small submodel
$ I$
-small submodel
![]() $ \mathcal {M}_{0} $
of
$ \mathcal {M}_{0} $
of
![]() $\mathcal {M}$
, if
$\mathcal {M}$
, if
![]() $ I\subsetneq M_{0} $
then
$ I\subsetneq M_{0} $
then
![]() $ M_{0} $
is mixed in
$ M_{0} $
is mixed in
![]() $ \mathcal {M.} $
(Since if
$ \mathcal {M.} $
(Since if
![]() $ M_{0}:=\{(a)_{i}: \ i\in I\} $
, and
$ M_{0}:=\{(a)_{i}: \ i\in I\} $
, and
![]() $ A:=\{i\in I: \ \mathcal {M}\models \neg i\mathrm {E}(a)_{i} \} $
, then
$ A:=\{i\in I: \ \mathcal {M}\models \neg i\mathrm {E}(a)_{i} \} $
, then
![]() $A\in \mathrm {SSy}_{I}(\mathcal {M})\setminus \mathrm {SSy}_{I}(\mathcal {M}_{0}) $
. So
$A\in \mathrm {SSy}_{I}(\mathcal {M})\setminus \mathrm {SSy}_{I}(\mathcal {M}_{0}) $
. So
![]() $ \mathcal {M}_{0} $
cannot be an initial segment of
$ \mathcal {M}_{0} $
cannot be an initial segment of
![]() $ \mathcal {M.} $
)
$ \mathcal {M.} $
)
In the following lemma we will show that in the definition of I-small, if I is a strong cut or it is equal to
![]() $ \mathbb {N} $
, then the condition
$ \mathbb {N} $
, then the condition
![]() $ (a)_{i}\neq (a)_{j} $
for all distinct
$ (a)_{i}\neq (a)_{j} $
for all distinct
![]() $ i,j\in I $
, can be eliminated:
$ i,j\in I $
, can be eliminated:
Lemma 3.1. Suppose
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is nonstandard,
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is nonstandard,
![]() $ I\subsetneq _{e}\mathcal {M} $
,
$ I\subsetneq _{e}\mathcal {M} $
,
![]() $ \mathcal {M}_{0} $
is a submodel of
$ \mathcal {M}_{0} $
is a submodel of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ M_{0}=\lbrace (a)_{i}:\ i\in I\rbrace $
for some
$ M_{0}=\lbrace (a)_{i}:\ i\in I\rbrace $
for some
![]() $ a\in M $
. Then the following hold:
$ a\in M $
. Then the following hold:
-
(1) If
 $ I=\mathbb {N} $
, then
$ I=\mathbb {N} $
, then
 $ \mathcal {M}_{0} $
is small.
$ \mathcal {M}_{0} $
is small. -
(2) If I is strong in
 $\mathcal {M}$
, then
$\mathcal {M}$
, then
 $ \mathcal {M}_{0}$
is
$ \mathcal {M}_{0}$
is
 $ I$
-small.
$ I$
-small.
Proof First, we will inductively define the following
![]() $ \Delta _{0}$
-function (with parameters) in
$ \Delta _{0}$
-function (with parameters) in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
 $$ \begin{align*} &\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\qquad g(0):=(a)_{0} , \\&\qquad\quad\qquad\quad\qquad\qquad\qquad\qquad\qquad\qquad \text{and}\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad g(x+1):=y \text{ iff } \\&\exists r<\mathrm{Len}(a) \left(\begin{array}{@{}c@{}} y=(a)_{r} \ \wedge \\ r= \mu_{z}\left(\begin{array}{@{}c@{}} \exists u<z \left(\begin{array}{@{}c@{}}g(x)=(a)_{u} \ \wedge \\ \forall w<z \ ( (a)_{w}\neq (a)_{z} \wedge \exists v\leq u ((a)_{w}=(a)_{v}) )\end{array}\right) \end{array}\right) \end{array}\right). \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\qquad g(0):=(a)_{0} , \\&\qquad\quad\qquad\quad\qquad\qquad\qquad\qquad\qquad\qquad \text{and}\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad g(x+1):=y \text{ iff } \\&\exists r<\mathrm{Len}(a) \left(\begin{array}{@{}c@{}} y=(a)_{r} \ \wedge \\ r= \mu_{z}\left(\begin{array}{@{}c@{}} \exists u<z \left(\begin{array}{@{}c@{}}g(x)=(a)_{u} \ \wedge \\ \forall w<z \ ( (a)_{w}\neq (a)_{z} \wedge \exists v\leq u ((a)_{w}=(a)_{v}) )\end{array}\right) \end{array}\right) \end{array}\right). \end{align*} $$
Note that by the way we defined
![]() $ g $
, its domain is an initial segment of
$ g $
, its domain is an initial segment of
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ {\mathrm {Dom}(g)\leq \mathrm {Len}(a)} $
. Moreover, since I and
$ {\mathrm {Dom}(g)\leq \mathrm {Len}(a)} $
. Moreover, since I and
![]() $ M_{0} $
are not
$ M_{0} $
are not
![]() $ \Delta _{0}$
-definable in
$ \Delta _{0}$
-definable in
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $ I\subsetneq \mathrm {Dom}(g) $
. So by
$ I\subsetneq \mathrm {Dom}(g) $
. So by
![]() $ \Sigma _{1}$
-induction in
$ \Sigma _{1}$
-induction in
![]() $\mathcal {M}$
, we can find some
$\mathcal {M}$
, we can find some
![]() $ d\in M $
such that
$ d\in M $
such that
![]() $ (d)_{i}=g(i) $
for every
$ (d)_{i}=g(i) $
for every
![]() $ i\in I $
. Clearly,
$ i\in I $
. Clearly,
![]() $ (d)_{i}\neq (d)_{j} $
for every distinct
$ (d)_{i}\neq (d)_{j} $
for every distinct
![]() $ i,j\in I $
, and
$ i,j\in I $
, and
![]() $ {M_{0}\subseteq \lbrace (d)_{i}: \ i\in I\rbrace } $
. Now, in each case of the statement of the theorem we will prove that
$ {M_{0}\subseteq \lbrace (d)_{i}: \ i\in I\rbrace } $
. Now, in each case of the statement of the theorem we will prove that
![]() $ \lbrace (d)_{i}: \ i\in I\rbrace \subseteq M_{0} $
:
$ \lbrace (d)_{i}: \ i\in I\rbrace \subseteq M_{0} $
:
-
(1) Suppose
 $ I=\mathbb {N} $
. If
$ I=\mathbb {N} $
. If
 $ \lbrace (d)_{n}: \ n\in \mathbb {N}\rbrace \nsubseteq M_{0} $
, then there exists the least number
$ \lbrace (d)_{n}: \ n\in \mathbb {N}\rbrace \nsubseteq M_{0} $
, then there exists the least number
 $ n\in \mathbb {N} $
such that
$ n\in \mathbb {N} $
such that
 $ (d)_{n}\notin M_{0} $
. So by the definition of
$ (d)_{n}\notin M_{0} $
. So by the definition of
 $ g $
, there exist some
$ g $
, there exist some
 $ m\in \mathbb {N} $
and some
$ m\in \mathbb {N} $
and some
 $ r\in M\setminus \mathbb {N} $
such that
$ r\in M\setminus \mathbb {N} $
such that
 ${ (d)_{n-1}=(a)_{m}} $
and
${ (d)_{n-1}=(a)_{m}} $
and
 $ (d)_{n}=(a)_{r} $
. Therefore, by the definition of
$ (d)_{n}=(a)_{r} $
. Therefore, by the definition of
 $ g $
, it holds that
$ g $
, it holds that
 $ M_{0}=\lbrace (a)_{0},\ldots ,(a)_{m}\rbrace $
, which is a contradiction.
$ M_{0}=\lbrace (a)_{0},\ldots ,(a)_{m}\rbrace $
, which is a contradiction. -
(2) In the general case with the extra assumption that I is strong in
 $\mathcal {M}$
, consider the following partial
$\mathcal {M}$
, consider the following partial
 $ \Delta _{0}$
-function in
$ \Delta _{0}$
-function in
 $\mathcal {M}$
: Since I is strong and
$\mathcal {M}$
: Since I is strong and $$ \begin{align*} h(x):=\mu_{r}( (d)_{x}=(a)_{r}). \end{align*} $$
$$ \begin{align*} h(x):=\mu_{r}( (d)_{x}=(a)_{r}). \end{align*} $$
 $ I\subseteq \mathrm {dom}(h) $
(because
$ I\subseteq \mathrm {dom}(h) $
(because
 $ g $
is well-defined on I), there exists some
$ g $
is well-defined on I), there exists some
 $ e\in M $
such that
$ e\in M $
such that
 $ h(i)\in I$
iff
$ h(i)\in I$
iff
 $ h(i)<e $
, for all
$ h(i)<e $
, for all
 $ i\in I $
. Moreover, by the definition of
$ i\in I $
. Moreover, by the definition of
 $ d$
,
$ d$
,
 $g $
and
$g $
and
 $ h $
, for every
$ h $
, for every
 $ i\in I $
it holds that
$ i\in I $
it holds that
 $ (d)_{i}=(a)_{h(i)} $
. So it suffices to prove that
$ (d)_{i}=(a)_{h(i)} $
. So it suffices to prove that
 $ h(i)<e $
for every
$ h(i)<e $
for every
 $ i\in I $
. Suppose not; so there exists some
$ i\in I $
. Suppose not; so there exists some
 $ i_{0}\in I $
which is the least element of
$ i_{0}\in I $
which is the least element of
 $ M $
such that
$ M $
such that
 $ h(i_{0})>e $
. Now, by the way we defined
$ h(i_{0})>e $
. Now, by the way we defined
 $ g $
and
$ g $
and
 $ h $
, it holds that Therefore,
$ h $
, it holds that Therefore, $$ \begin{align*} \mathcal{M}\models\forall i<h(i_{0}) \ ((a)_{i}\neq(a)_{h(i_{0})}\wedge \exists j\leq h(i_{0}-1) ((a)_{i}=(a)_{j})). \end{align*} $$
$$ \begin{align*} \mathcal{M}\models\forall i<h(i_{0}) \ ((a)_{i}\neq(a)_{h(i_{0})}\wedge \exists j\leq h(i_{0}-1) ((a)_{i}=(a)_{j})). \end{align*} $$
 $ M_{0}=\lbrace x\in M: \ \mathcal {M}\models \exists i\leq h(i_{0}-1) \ x=(a)_{i} \rbrace $
. So
$ M_{0}=\lbrace x\in M: \ \mathcal {M}\models \exists i\leq h(i_{0}-1) \ x=(a)_{i} \rbrace $
. So
 $ M_{0} $
is
$ M_{0} $
is
 $ \Delta _{0}$
-definable in
$ \Delta _{0}$
-definable in
 $\mathcal {M}$
, which is a contradiction.
$\mathcal {M}$
, which is a contradiction.
In the following theorem, we will show that when I is strong, the basic properties which hold for small submodels, also hold for
![]() $ I$
-small ones.
$ I$
-small ones.
Theorem 3.2. Let
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be nonstandard, and let I be a strong cut of
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be nonstandard, and let I be a strong cut of
![]() $\mathcal {M}$
. Then:
$\mathcal {M}$
. Then:
-
(1) For every
 $ a\in M $
,
$ a\in M $
,
 $ \mathrm {K}^{1}(\mathcal {M};I\cup \lbrace a\rbrace ) $
is
$ \mathrm {K}^{1}(\mathcal {M};I\cup \lbrace a\rbrace ) $
is
 $ I$
-small.
$ I$
-small. -
(2) If
 $ \mathcal {M}_{0} $
is an
$ \mathcal {M}_{0} $
is an
 $ I$
-small submodel of
$ I$
-small submodel of
 $\mathcal {M}$
, then
$\mathcal {M}$
, then
 $ I\subseteq M_{0} $
.
$ I\subseteq M_{0} $
. -
(3) If
 $ \mathcal {M}\models \mathrm {PA} $
is countable and recursively saturated, then there exists some
$ \mathcal {M}\models \mathrm {PA} $
is countable and recursively saturated, then there exists some
 $ I$
-small elementary submodel of
$ I$
-small elementary submodel of
 $\mathcal {M}$
which is not of the form of
$\mathcal {M}$
which is not of the form of
 $ \mathrm {K}(\mathcal {M}; I\cup \lbrace a\rbrace ) $
for any
$ \mathrm {K}(\mathcal {M}; I\cup \lbrace a\rbrace ) $
for any
 $ a\in M $
.
$ a\in M $
.
Proof
-
(1) First fix some arbitrary
 $ s>I $
. So by using strong
$ s>I $
. So by using strong
 $ \Sigma _{1}$
-Collection in
$ \Sigma _{1}$
-Collection in
 $\mathcal {M}$
for the formula
$\mathcal {M}$
for the formula
 $ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(i,a,z)) $
, we will find some
$ \mathrm {Sat}_{\Delta _{0}}(\delta _{r}(i,a,z)) $
, we will find some
 $ b\in M $
such that Then, by using
$ b\in M $
such that Then, by using $$ \begin{align*} \mathcal{M}\models\forall \langle r,i\rangle<s \ ([f_{r}(i,a)\downarrow]\rightarrow[f_{r}(i,a)\downarrow]^{<b}). \end{align*} $$
$$ \begin{align*} \mathcal{M}\models\forall \langle r,i\rangle<s \ ([f_{r}(i,a)\downarrow]\rightarrow[f_{r}(i,a)\downarrow]^{<b}). \end{align*} $$
 $ \Sigma _{1}$
-induction we observe that
$ \Sigma _{1}$
-induction we observe that
 $ \mathcal {M}\models \exists y \ \forall \langle r,i\rangle <s \ \varphi (y,r,i,a,b) $
, in which
$ \mathcal {M}\models \exists y \ \forall \langle r,i\rangle <s \ \varphi (y,r,i,a,b) $
, in which
 $ \varphi (y,r,i,a,b) $
is the following
$ \varphi (y,r,i,a,b) $
is the following
 $ \Delta _{0}$
-formula: As a result, if
$ \Delta _{0}$
-formula: As a result, if $$ \begin{align*} \left( \begin{array}{@{}c@{}} ([f_{r}(i,a)\downarrow]^{<b}\rightarrow(y)_{ \langle r,i\rangle}=f_{r}(i,a)) \ \wedge \ (\neg[f_{r}(i,a)\downarrow]^{<b}\rightarrow(y)_{ \langle r,i\rangle}=0) \end{array}\right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{@{}c@{}} ([f_{r}(i,a)\downarrow]^{<b}\rightarrow(y)_{ \langle r,i\rangle}=f_{r}(i,a)) \ \wedge \ (\neg[f_{r}(i,a)\downarrow]^{<b}\rightarrow(y)_{ \langle r,i\rangle}=0) \end{array}\right). \end{align*} $$
 $ d\in M $
is such that
$ d\in M $
is such that
 $ \mathcal {M}\models \forall \langle r,i\rangle <s \ \varphi (d,r,i,a,b) $
, then So by Lemma 3.1,
$ \mathcal {M}\models \forall \langle r,i\rangle <s \ \varphi (d,r,i,a,b) $
, then So by Lemma 3.1, $$ \begin{align*} \mathrm{K}^{1}(\mathcal{M}; I\cup\lbrace a\rbrace)=\{(d)_{i}: \ i\in I \}. \end{align*} $$
$$ \begin{align*} \mathrm{K}^{1}(\mathcal{M}; I\cup\lbrace a\rbrace)=\{(d)_{i}: \ i\in I \}. \end{align*} $$
 $ \mathrm {K}^{1}(\mathcal {M}; I\cup \lbrace a\rbrace ) $
is
$ \mathrm {K}^{1}(\mathcal {M}; I\cup \lbrace a\rbrace ) $
is
 $ I$
-small in
$ I$
-small in
 $\mathcal {M}$
.
$\mathcal {M}$
.
-
(2) The exact argument used in [Reference Enayat4, Theorem 4.5.1] works here: let
 $ { M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
for some
$ { M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
for some
 $ a\in M $
such that
$ a\in M $
such that
 $ (a)_{i}\neq (a)_{j} $
for all distinct
$ (a)_{i}\neq (a)_{j} $
for all distinct
 $ i, j\in I $
. Then put Since
$ i, j\in I $
. Then put Since $$ \begin{align*} { Z:=\lbrace \langle y,z\rangle\in M: \ \mathcal{M}\models (a)_{y}=z \rbrace }. \end{align*} $$
$$ \begin{align*} { Z:=\lbrace \langle y,z\rangle\in M: \ \mathcal{M}\models (a)_{y}=z \rbrace }. \end{align*} $$
 $ Z $
is
$ Z $
is
 $ \Delta _{0}$
-definable in
$ \Delta _{0}$
-definable in
 $\mathcal {M}$
, then
$\mathcal {M}$
, then
 $ X:= I\cap Z \in \mathrm {SSy}_{ I}(\mathcal {M}) $
. As a result, because
$ X:= I\cap Z \in \mathrm {SSy}_{ I}(\mathcal {M}) $
. As a result, because
 $ I $
is strong in
$ I $
is strong in
 $\mathcal {M}$
,
$\mathcal {M}$
,
 $ ( I; X)\models \mathrm {PA}^{*} $
. Now, suppose
$ ( I; X)\models \mathrm {PA}^{*} $
. Now, suppose
 $ I\nsubseteq M_{0} $
. So
$ I\nsubseteq M_{0} $
. So
 $ ( I; X)\models \exists x \ (\forall y \ \langle y,x\rangle \notin X) $
. Let
$ ( I; X)\models \exists x \ (\forall y \ \langle y,x\rangle \notin X) $
. Let
 $ ( I, X)\models \textbf {x}_{0}:=\mu _{x} ( \forall y \ \langle y,x\rangle \notin X) $
. Therefore,
$ ( I, X)\models \textbf {x}_{0}:=\mu _{x} ( \forall y \ \langle y,x\rangle \notin X) $
. Therefore,
 $ \textbf {x}_{0}\notin M_{0} $
. So since
$ \textbf {x}_{0}\notin M_{0} $
. So since
 $ \textbf {x}_{0}\neq 0 $
, and by the definition of
$ \textbf {x}_{0}\neq 0 $
, and by the definition of
 $ \textbf {x}_{0} $
, we conclude that
$ \textbf {x}_{0} $
, we conclude that
 $ \textbf {x}_{0}-1\in M_{0} $
, which contradicts the fact that
$ \textbf {x}_{0}-1\in M_{0} $
, which contradicts the fact that
 $ \mathcal {M}_{0} $
is a submodel of
$ \mathcal {M}_{0} $
is a submodel of
 $\mathcal {M}$
.
$\mathcal {M}$
.
-
(3) We will generalize the method used in [Reference Kossak and Schmerl12, Proposition 2.10]: let
 $ S $
be a nonstandard partial inductive satisfaction class for
$ S $
be a nonstandard partial inductive satisfaction class for
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ (\mathcal {M}; S) $
is recursively saturated. Put
$ (\mathcal {M}; S) $
is recursively saturated. Put
 $ \mathcal {M}^{*}:=(\mathcal {M}; S) $
, and
$ \mathcal {M}^{*}:=(\mathcal {M}; S) $
, and
 $ \mathcal {N}:=\mathrm {K}(\mathcal {M}^{*};I\cup \{s\}) $
for some
$ \mathcal {N}:=\mathrm {K}(\mathcal {M}^{*};I\cup \{s\}) $
for some
 $ s>I $
. First, note that
$ s>I $
. First, note that
 $ N $
is
$ N $
is
 $ I$
-small in
$ I$
-small in
 $\mathcal {M}$
: since
$\mathcal {M}$
: since
 $ \mathcal {M}^{*} $
is a countable recursively saturated model of
$ \mathcal {M}^{*} $
is a countable recursively saturated model of
 $ \mathrm {PA}^{*}$
, so it also possesses an inductive satisfaction class. Moreover, I is also strong in
$ \mathrm {PA}^{*}$
, so it also possesses an inductive satisfaction class. Moreover, I is also strong in
 $ \mathcal {M}^{*} $
. Therefore, by repeating the argument used in the proof of part (1) of this theorem, and Lemma 3.1(2), we can show that
$ \mathcal {M}^{*} $
. Therefore, by repeating the argument used in the proof of part (1) of this theorem, and Lemma 3.1(2), we can show that
 $ N $
is
$ N $
is
 $ I$
-small in
$ I$
-small in
 $\mathcal {M}$
.
$\mathcal {M}$
.Moreover, on one hand, it is easy to see that
 $ S\cap N $
is a nonstandard satisfaction class for the
$ S\cap N $
is a nonstandard satisfaction class for the
 $ \mathcal {L}_{A}$
-structure
$ \mathcal {L}_{A}$
-structure
 $ \mathcal {N} $
. So
$ \mathcal {N} $
. So
 $ \mathcal {N} $
is also a recursively saturated model of
$ \mathcal {N} $
is also a recursively saturated model of
 $\mathrm {PA}$
. On the other hand, I is a proper initial segment of
$\mathrm {PA}$
. On the other hand, I is a proper initial segment of
 $ \mathcal {N} $
(because
$ \mathcal {N} $
(because
 $ s>I $
). Therefore,
$ s>I $
). Therefore,
 $ \mathcal {N} $
is of the form of
$ \mathcal {N} $
is of the form of
 $ \mathrm {K}(\mathcal {M};I\cup \{a\}) $
for no
$ \mathrm {K}(\mathcal {M};I\cup \{a\}) $
for no
 $ a\in M $
.
$ a\in M $
.
Remark 2. In part (2) of the above theorem, as the anonymous referee suggested, we do not need the whole strength of
![]() $ \mathrm {PA}^{*} $
; it suffices that
$ \mathrm {PA}^{*} $
; it suffices that
![]() $ (I;X)\models \mathrm {I}\Sigma _{1} $
. As a result, if I is a semiregular cut of
$ (I;X)\models \mathrm {I}\Sigma _{1} $
. As a result, if I is a semiregular cut of
![]() $\mathcal {M}$
, then part (2) of the above theorem holds (for the definition of a semiregular cut and their properties, see [Reference Kossak and Schmerl13]).
$\mathcal {M}$
, then part (2) of the above theorem holds (for the definition of a semiregular cut and their properties, see [Reference Kossak and Schmerl13]).
The following lemma will be useful in the proof of the main theorem of this section:
Lemma 3.3. Suppose
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
,
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
,
![]() $ I $
is a strong cut of
$ I $
is a strong cut of
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ a\in M\setminus I $
such that
$ a\in M\setminus I $
such that
![]() $ (a)_{i}\neq (a)_{j} $
for all distinct
$ (a)_{i}\neq (a)_{j} $
for all distinct
![]() $ i,j\in I $
. Moreover, let
$ i,j\in I $
. Moreover, let
![]() $ { M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
be a
$ { M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
be a
![]() $ \Sigma _{1} $
-elementary submodel of
$ \Sigma _{1} $
-elementary submodel of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $ X\subseteq M_{0}$
be coded in
$ X\subseteq M_{0}$
be coded in
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ i_{0}\in I $
such that
$ i_{0}\in I $
such that
![]() $ i<i_{0}$
for all
$ i<i_{0}$
for all
![]() $ (a)_{i}\in X $
. Then
$ (a)_{i}\in X $
. Then
![]() $ X $
is coded in
$ X $
is coded in
![]() $ \mathcal {M}_{0} $
.
$ \mathcal {M}_{0} $
.
Proof Suppose
![]() $ \alpha \in M $
codes
$ \alpha \in M $
codes
![]() $ X $
in
$ X $
in
![]() $\mathcal {M}$
. So
$\mathcal {M}$
. So
 $ \mathcal {M}\models \overset {\delta (\alpha ,\sigma ,i_{1})}{\overbrace {\alpha =\sum _{i<i_{1}}2^{(\sigma )_{i}}} }$
, in which
$ \mathcal {M}\models \overset {\delta (\alpha ,\sigma ,i_{1})}{\overbrace {\alpha =\sum _{i<i_{1}}2^{(\sigma )_{i}}} }$
, in which
![]() $ i_{1}=\mathrm {Card}( X)\leq i_{0} $
and
$ i_{1}=\mathrm {Card}( X)\leq i_{0} $
and
![]() $ \sigma :=\langle x: \ x\mathrm {E}\alpha \rangle $
(so
$ \sigma :=\langle x: \ x\mathrm {E}\alpha \rangle $
(so
![]() $ \mathrm {Len}(\sigma )=i_{1} $
). Since
$ \mathrm {Len}(\sigma )=i_{1} $
). Since
![]() $ \delta (x,y,z) $
is a
$ \delta (x,y,z) $
is a
![]() $ \Delta _{0}$
-formula and
$ \Delta _{0}$
-formula and
![]() $ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, it suffices to prove that
$ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, it suffices to prove that
![]() $ \sigma \in M_{0} $
. For this purpose let
$ \sigma \in M_{0} $
. For this purpose let
![]() $ Y:=\{i<i_{0}:\ \mathcal {M}\models (a)_{i}\mathrm {E}\alpha \} $
. Then there exists some
$ Y:=\{i<i_{0}:\ \mathcal {M}\models (a)_{i}\mathrm {E}\alpha \} $
. Then there exists some
![]() $ \gamma \in I $
which codes
$ \gamma \in I $
which codes
![]() $ Y $
.
$ Y $
.
Now, we define
 $$ \begin{align*} h(z) := \begin{cases} \mu_{u}(\langle (a)_{x}: \ x\mathrm{E}z \rangle=(a)_{u}\wedge u<\mathrm{Len}(a)), & \text{if } \mathcal{M}\models\exists u<\mathrm{Len}(a) \ \langle (a)_{x}: \ x\mathrm{E}z \rangle=(a)_{u}, \\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} h(z) := \begin{cases} \mu_{u}(\langle (a)_{x}: \ x\mathrm{E}z \rangle=(a)_{u}\wedge u<\mathrm{Len}(a)), & \text{if } \mathcal{M}\models\exists u<\mathrm{Len}(a) \ \langle (a)_{x}: \ x\mathrm{E}z \rangle=(a)_{u}, \\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
Since
![]() $ I $
is strong in
$ I $
is strong in
![]() $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
![]() $ e $
such that
$ e $
such that
![]() $ h(i)>e $
iff
$ h(i)>e $
iff
![]() $ h(i)>I $
, for all
$ h(i)>I $
, for all
![]() $ i\in I $
. We claim that
$ i\in I $
. We claim that
![]() $ \mathcal {M}\models \forall x \ \varphi (x,a,\gamma ,e) $
, where
$ \mathcal {M}\models \forall x \ \varphi (x,a,\gamma ,e) $
, where
![]() $\varphi (x,a,\gamma ,e) $
is the following
$\varphi (x,a,\gamma ,e) $
is the following
![]() $ \Delta _{0}$
-formula:
$ \Delta _{0}$
-formula:
Therefore,
![]() $ \mathcal {M}\models \varphi (\sigma ,a,\gamma ,e) $
, which implies that
$ \mathcal {M}\models \varphi (\sigma ,a,\gamma ,e) $
, which implies that
![]() $ \sigma =(a)_{c} $
for some
$ \sigma =(a)_{c} $
for some
![]() $ c<\min \{e,\mathrm {Len}(a)\} $
. So
$ c<\min \{e,\mathrm {Len}(a)\} $
. So
![]() $ \sigma =(a)_{h(\gamma )} $
and
$ \sigma =(a)_{h(\gamma )} $
and
![]() $ h(\gamma )<e $
, which implies that
$ h(\gamma )<e $
, which implies that
![]() $ \sigma \in M_{_{0}} $
.
$ \sigma \in M_{_{0}} $
.
In order to prove the above claim, we will use
![]() $ \Delta _{0}$
-induction inside
$ \Delta _{0}$
-induction inside
![]() $\mathcal {M}$
: let
$\mathcal {M}$
: let
![]() $ \textbf {x}\in M $
such that
$ \textbf {x}\in M $
such that
![]() $ {\mathcal {M}\models \varphi (w,a,\gamma ,e)} $
for every
$ {\mathcal {M}\models \varphi (w,a,\gamma ,e)} $
for every
![]() $ w<\textbf {x} $
, and
$ w<\textbf {x} $
, and
![]() $ \mathcal {M}\models \forall y<\mathrm {Len}(\textbf {x}) \ \exists z\mathrm {E}\gamma \ ((\textbf {x})_{y}=(a)_{z}) $
. So by induction hypothesis
$ \mathcal {M}\models \forall y<\mathrm {Len}(\textbf {x}) \ \exists z\mathrm {E}\gamma \ ((\textbf {x})_{y}=(a)_{z}) $
. So by induction hypothesis
![]() ${\mathcal {M}\models \textbf {x}\upharpoonright _{\mathrm {Len}(\textbf {x})-1}=(a)_{\textbf {z}} }$
for some
${\mathcal {M}\models \textbf {x}\upharpoonright _{\mathrm {Len}(\textbf {x})-1}=(a)_{\textbf {z}} }$
for some
![]() $ \textbf {z}<\min \{e,\mathrm {Len}(a)\} $
. Then, we put
$ \textbf {z}<\min \{e,\mathrm {Len}(a)\} $
. Then, we put
![]() $ Z:=\{i<\gamma : \ \mathcal {M}\models \exists y<\mathrm {Len}(\textbf {x})-1 \ (\textbf {x})_{y}=(a)_{i}\} $
, and let
$ Z:=\{i<\gamma : \ \mathcal {M}\models \exists y<\mathrm {Len}(\textbf {x})-1 \ (\textbf {x})_{y}=(a)_{i}\} $
, and let
![]() $ \textbf {z}_{0}\in I $
code
$ \textbf {z}_{0}\in I $
code
![]() $ Z $
. As a result,
$ Z $
. As a result,
![]() $ h(\textbf {z}_{0})\leq \textbf {z}<\min \{e,\mathrm {Len}(a)\} $
, which implies that
$ h(\textbf {z}_{0})\leq \textbf {z}<\min \{e,\mathrm {Len}(a)\} $
, which implies that
![]() $ \textbf {x}\upharpoonright _{\mathrm {Len}(\textbf {x})-1}=(a)_{h(\textbf {z}_{0})}\in M_{0} $
. So since
$ \textbf {x}\upharpoonright _{\mathrm {Len}(\textbf {x})-1}=(a)_{h(\textbf {z}_{0})}\in M_{0} $
. So since
![]() $ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, then
$ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, then
![]() $ \textbf {x} $
is in
$ \textbf {x} $
is in
![]() $ M_{0} $
. Therefore,
$ M_{0} $
. Therefore,
![]() $ \textbf {x}=(a)_{i} $
for some
$ \textbf {x}=(a)_{i} $
for some
![]() $ i\in I<\min \{e,\mathrm {Len}(a)\} $
.
$ i\in I<\min \{e,\mathrm {Len}(a)\} $
.
Now we are ready to prove the main theorem and corollary of this section. The method we use for proving Theorem 3.4 is a combination of the back-and-forth method used in [Reference Bahrami and Enayat1, Theorem 6.1] and [Reference Kaye, Kossak and Kotlarski8, Theorem 5.6].
Theorem 3.4. Assume
![]() $ \mathcal {N}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard,
$ \mathcal {N}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard,
![]() $ I $
is a strong cut of
$ I $
is a strong cut of
![]() $ \mathcal {N} $
, and
$ \mathcal {N} $
, and
![]() $ \mathcal {N}_{0} $
is an
$ \mathcal {N}_{0} $
is an
![]() $ I$
-small
$ I$
-small
![]() $ \Sigma _{1} $
-elementary submodel of
$ \Sigma _{1} $
-elementary submodel of
![]() $ \mathcal {N} $
such that
$ \mathcal {N} $
such that
![]() $ I\neq N_{0} $
. If
$ I\neq N_{0} $
. If
![]() $ \mathcal {M}:=\mathrm {H}^{1}(\mathcal {N};N_{0}) $
, then there exists some proper initial self-embedding
$ \mathcal {M}:=\mathrm {H}^{1}(\mathcal {N};N_{0}) $
, then there exists some proper initial self-embedding
![]() $ j $
of
$ j $
of
![]() $ \mathcal {M} $
such that
$ \mathcal {M} $
such that
![]() $ { N_{0}=\mathrm {Fix}(j)} $
.
$ { N_{0}=\mathrm {Fix}(j)} $
.
In order to prove Theorem 3.4, we will first prove the following lemmas:
Lemma 3.4.1. Suppose
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $N_{0} $
,
$N_{0} $
,
![]() $ I, $
and
$ I, $
and
![]() $\mathcal {M}$
are as in Theorem 3.4. Then I is strong in
$\mathcal {M}$
are as in Theorem 3.4. Then I is strong in
![]() $\mathcal {M}$
and there exists some
$\mathcal {M}$
and there exists some
![]() $ a\in M $
such that
$ a\in M $
such that
![]() $ N_{0}=\{(a)_{i}: i\in I\} $
and
$ N_{0}=\{(a)_{i}: i\in I\} $
and
![]() $ (a)_{i}\neq (a)_{i} $
for distinct
$ (a)_{i}\neq (a)_{i} $
for distinct
![]() $ i,j\in I $
.
$ i,j\in I $
.
Proof By Theorem 2.1,
![]() $\mathcal {M}$
is a
$\mathcal {M}$
is a
![]() $ \Sigma _{1}$
-elementary initial segment of
$ \Sigma _{1}$
-elementary initial segment of
![]() $ \mathcal {N} $
such that
$ \mathcal {N} $
such that
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
. So it is easy to see that I is also strong in
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
. So it is easy to see that I is also strong in
![]() $\mathcal {M}$
. Moreover, since
$\mathcal {M}$
. Moreover, since
![]() $ N_{0}\neq I $
, by using
$ N_{0}\neq I $
, by using
![]() $ \Sigma _{1} $
-Overspill in
$ \Sigma _{1} $
-Overspill in
![]() $\mathcal {M}$
we can find the desired
$\mathcal {M}$
we can find the desired
![]() $ a\in M $
.
$ a\in M $
.
Lemma 3.4.2. Suppose
![]() $ \mathcal {N} $
,
$ \mathcal {N} $
,
![]() $ N_{0} $
, I,
$ N_{0} $
, I,
![]() $ \mathcal {M,} $
and
$ \mathcal {M,} $
and
![]() $ a\in M $
are as in Theorem 3.4 and Lemma 3.4.1. Moreover, let
$ a\in M $
are as in Theorem 3.4 and Lemma 3.4.1. Moreover, let
![]() $ b\in M $
,
$ b\in M $
,
![]() $ \bar {u}:=u_{1},\ldots ,u_{n,} $
and
$ \bar {u}:=u_{1},\ldots ,u_{n,} $
and
![]() $ \bar {v}:=v_{1},\ldots ,v_{n} <b $
be finite tuples in
$ \bar {v}:=v_{1},\ldots ,v_{n} <b $
be finite tuples in
![]() $ M $
. Then the following holds:
$ M $
. Then the following holds:
-
(i) For every
 $ m\in M $
there exists some
$ m\in M $
there exists some
 $ \alpha \in M $
such that
$ \alpha \in M $
such that
 $ I\cap \alpha _{\mathrm {E}} $
equals to the following set:
$ I\cap \alpha _{\mathrm {E}} $
equals to the following set:  $$ \begin{align*}\kern-27pt C:=\left\lbrace \langle r,i\rangle\in I: \ \mathcal{M}\models[f_{r}(\bar{u},m,(a)_{i})\downarrow] \ \text{and} \ f_{r}(\bar{u},m,(a)_{i})\notin\mathrm{K}^{1}(\mathcal{M}; N_{0}\cup\{\bar{u}\}) \right\rbrace.\end{align*} $$
$$ \begin{align*}\kern-27pt C:=\left\lbrace \langle r,i\rangle\in I: \ \mathcal{M}\models[f_{r}(\bar{u},m,(a)_{i})\downarrow] \ \text{and} \ f_{r}(\bar{u},m,(a)_{i})\notin\mathrm{K}^{1}(\mathcal{M}; N_{0}\cup\{\bar{u}\}) \right\rbrace.\end{align*} $$
-
(ii) For every
 $ m'\in M $
there exists some
$ m'\in M $
there exists some
 $ \alpha '\in M $
such that
$ \alpha '\in M $
such that
 $ I\cap \alpha ^{\prime }_{\mathrm {E}} $
equals to the following set:
$ I\cap \alpha ^{\prime }_{\mathrm {E}} $
equals to the following set:  $$ \begin{align*}\kern-27pt C':=\lbrace\langle r,i\rangle\in I: \ \mathcal{M}\models[f_{r}(\bar{v},m',(a)_{i})\downarrow]^{<b} \ \text{and} \ f_{r}(\bar{v},m',(a)_{i})\notin\mathrm{K}^{1}(\mathcal{M}; N_{0}\cup\{\bar{v}\})\rbrace.\end{align*} $$
$$ \begin{align*}\kern-27pt C':=\lbrace\langle r,i\rangle\in I: \ \mathcal{M}\models[f_{r}(\bar{v},m',(a)_{i})\downarrow]^{<b} \ \text{and} \ f_{r}(\bar{v},m',(a)_{i})\notin\mathrm{K}^{1}(\mathcal{M}; N_{0}\cup\{\bar{v}\})\rbrace.\end{align*} $$
Proof We will prove part (i), and part (ii) will be proved similarly. Let
 $$ \begin{align*} R:=\left\lbrace \langle \langle r,i\rangle,k,t\rangle\in I: \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} ([f_{r}(\bar{u},m,(a)_{i})\downarrow]\wedge [f_{t}(\bar{u},(a)_{k})\downarrow])\rightarrow\\ f_{r}(\bar{u},m,(a)_{i})=f_{t}(\bar{u},(a)_{k}) \end{array}\right)\right\rbrace. \end{align*} $$
$$ \begin{align*} R:=\left\lbrace \langle \langle r,i\rangle,k,t\rangle\in I: \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} ([f_{r}(\bar{u},m,(a)_{i})\downarrow]\wedge [f_{t}(\bar{u},(a)_{k})\downarrow])\rightarrow\\ f_{r}(\bar{u},m,(a)_{i})=f_{t}(\bar{u},(a)_{k}) \end{array}\right)\right\rbrace. \end{align*} $$
On one hand, since R is
![]() $\Pi _{1}$
-definable in
$\Pi _{1}$
-definable in
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $ R\in \mathrm {SSy}_{ I}(\mathcal {M})$
. On the other hand, by Lemma 3.2(2), it holds that
$ R\in \mathrm {SSy}_{ I}(\mathcal {M})$
. On the other hand, by Lemma 3.2(2), it holds that
 $$ \begin{align*} { I\setminus C= \overset{ B}{\overbrace{\lbrace \langle r,i\rangle\in I: \ ( I, R)\models \exists k,t \ \langle\langle r, i\rangle,k,t\rangle\in R\rbrace}}}. \end{align*} $$
$$ \begin{align*} { I\setminus C= \overset{ B}{\overbrace{\lbrace \langle r,i\rangle\in I: \ ( I, R)\models \exists k,t \ \langle\langle r, i\rangle,k,t\rangle\in R\rbrace}}}. \end{align*} $$
Since I is strong in
![]() $\mathcal {M}$
, which implies that
$\mathcal {M}$
, which implies that
![]() $ (I,\mathrm {SSy}_{I}(\mathcal {M}))\models \mathrm {ACA}_{0} $
, and because
$ (I,\mathrm {SSy}_{I}(\mathcal {M}))\models \mathrm {ACA}_{0} $
, and because
![]() $ B $
is arithmetical in
$ B $
is arithmetical in
![]() $ R $
and
$ R $
and
![]() $ R\in \mathrm {SSy}_{ I}(\mathcal {M}) $
, we may deduce that
$ R\in \mathrm {SSy}_{ I}(\mathcal {M}) $
, we may deduce that
![]() $ B\in \mathrm {SSy}_{ I}(\mathcal {M}) $
, and consequently
$ B\in \mathrm {SSy}_{ I}(\mathcal {M}) $
, and consequently
![]() $ C\in \mathrm {SSy}_{ I}(\mathcal {M}) $
.
$ C\in \mathrm {SSy}_{ I}(\mathcal {M}) $
.
Lemma 3.4.3. Suppose
![]() $ \mathcal {N} $
,
$ \mathcal {N} $
,
![]() $ \mathrm {I} $
,
$ \mathrm {I} $
,
![]() $ N_{0} $
,
$ N_{0} $
,
![]() $ \mathcal {M,} $
and
$ \mathcal {M,} $
and
![]() $ a\in M $
are as in Theorem 3.4 and Lemma 3.4.1. Moreover, let
$ a\in M $
are as in Theorem 3.4 and Lemma 3.4.1. Moreover, let
![]() $ b\in M $
,
$ b\in M $
,
![]() $ \bar {u}:=u_{1},\ldots ,u_{n,} $
and
$ \bar {u}:=u_{1},\ldots ,u_{n,} $
and
![]() $ \bar {v}:=v_{1},\ldots ,v_{n} $
be finite tuples in
$ \bar {v}:=v_{1},\ldots ,v_{n} $
be finite tuples in
![]() $ M $
such that
$ M $
such that
![]() $ \mathrm{P}(\bar{u},\bar{v})\equiv [f(\bar{u},(a)_{i})\downarrow]\rightarrow[f(\bar{v},(a)_{i})\downarrow]^{<b} , \text{ for all } f\in\mathcal{F} \text{ and } i\in I ; $
$ \mathrm{P}(\bar{u},\bar{v})\equiv [f(\bar{u},(a)_{i})\downarrow]\rightarrow[f(\bar{v},(a)_{i})\downarrow]^{<b} , \text{ for all } f\in\mathcal{F} \text{ and } i\in I ; $
and
 $ \mathrm{Q}(\bar{u},\bar{v})\equiv \left(\begin{array}{@{}c@{}} [f(\bar{u},(a)_{i})\downarrow]\wedge [f(\bar{v},(a)_{i})\downarrow]^{<b} \wedge\\ f(\bar{u},(a)_{i})\notin N_{0} \end{array}\right) \Rightarrow{f(\bar{u},(a)_{i})\neq f(\bar{v},(a)_{i})},\ \text{for all}\ f\in\mathcal{F} \text{ and } \text{all } i\in I. $
$ \mathrm{Q}(\bar{u},\bar{v})\equiv \left(\begin{array}{@{}c@{}} [f(\bar{u},(a)_{i})\downarrow]\wedge [f(\bar{v},(a)_{i})\downarrow]^{<b} \wedge\\ f(\bar{u},(a)_{i})\notin N_{0} \end{array}\right) \Rightarrow{f(\bar{u},(a)_{i})\neq f(\bar{v},(a)_{i})},\ \text{for all}\ f\in\mathcal{F} \text{ and } \text{all } i\in I. $
Then the following holds:
-
(i) If
 $ (a)_{\mathrm {i}}\in N_{0} $
and
$ (a)_{\mathrm {i}}\in N_{0} $
and
 $ m\in M $
such that
$ m\in M $
such that
 $ m\leq t(\bar {u},(a)_{\mathrm {i}}) $
for some
$ m\leq t(\bar {u},(a)_{\mathrm {i}}) $
for some
 $ t\in \mathcal {F} $
and
$ t\in \mathcal {F} $
and
 $ \alpha \in M $
as in Lemma 3.4.2(i), then for every natural number
$ \alpha \in M $
as in Lemma 3.4.2(i), then for every natural number
 $ k>0 $
and any
$ k>0 $
and any
 $ (k+1) $
-many elements
$ (k+1) $
-many elements
 $ f,f_{n_{1}},\ldots ,f_{n_{k}} $
of
$ f,f_{n_{1}},\ldots ,f_{n_{k}} $
of
 $ \mathcal {F} $
and each
$ \mathcal {F} $
and each
 $ z\in N_{0} $
there exist some
$ z\in N_{0} $
there exist some
 $ s>I $
and some
$ s>I $
and some
 $ m'<b $
such that
$ m'<b $
such that
 $\mathcal {M}\models \Psi (f,f_{n_{1}},\ldots ,f_{n_{k}},\bar {u},m,\bar {v},m',b,a,s,\alpha ,z,(a)_{\mathrm {i}})$
, where
$\mathcal {M}\models \Psi (f,f_{n_{1}},\ldots ,f_{n_{k}},\bar {u},m,\bar {v},m',b,a,s,\alpha ,z,(a)_{\mathrm {i}})$
, where
 $\Psi $
is the following
$\Psi $
is the following
 $\Pi _{1}$
-formula:
$\Pi _{1}$
-formula:  $$ \begin{align*} \kern-2pt m'\leq t(\bar{v},(a)_{\mathrm{i}}) \ \wedge \left(\begin{array}{@{}c@{}} \forall i<s([f(\bar{u},m,(a)_{i},z)\downarrow]\rightarrow[f(\bar{v},m',(a)_{i},z)\downarrow]^{<b}) \ \wedge \\ \forall i<s \bigwedge_{t\leq k}\left(\begin{array}{@{}c@{}} ([f_{n_{t}}(\bar{v},m',(a)_{i})\downarrow]^{<b} \wedge \langle n_{t},i\rangle\mathrm{E}\alpha)\rightarrow \\ f_{n_{t}}(\bar{u},m,(a)_{i})\neq f_{n_{t}}(\bar{v},m',(a)_{i}) \end{array}\right)\end{array}\right). \end{align*} $$
$$ \begin{align*} \kern-2pt m'\leq t(\bar{v},(a)_{\mathrm{i}}) \ \wedge \left(\begin{array}{@{}c@{}} \forall i<s([f(\bar{u},m,(a)_{i},z)\downarrow]\rightarrow[f(\bar{v},m',(a)_{i},z)\downarrow]^{<b}) \ \wedge \\ \forall i<s \bigwedge_{t\leq k}\left(\begin{array}{@{}c@{}} ([f_{n_{t}}(\bar{v},m',(a)_{i})\downarrow]^{<b} \wedge \langle n_{t},i\rangle\mathrm{E}\alpha)\rightarrow \\ f_{n_{t}}(\bar{u},m,(a)_{i})\neq f_{n_{t}}(\bar{v},m',(a)_{i}) \end{array}\right)\end{array}\right). \end{align*} $$
-
(ii) If
 $ m'<\max \{\bar {v}\} $
and
$ m'<\max \{\bar {v}\} $
and
 $ \alpha '\in M $
as in Lemma 3.4.2(ii), then for every natural number
$ \alpha '\in M $
as in Lemma 3.4.2(ii), then for every natural number
 $ {k>0} $
and any
$ {k>0} $
and any
 $ (k+1) $
-many elements
$ (k+1) $
-many elements
 $ f,f_{n_{1}},\ldots ,f_{n_{k}} $
of
$ f,f_{n_{1}},\ldots ,f_{n_{k}} $
of
 $ \mathcal {F} $
and each
$ \mathcal {F} $
and each
 $ z\in N_{0} $
there exist some
$ z\in N_{0} $
there exist some
 $ s>I $
and some
$ s>I $
and some
 $ m<\max \{\bar {u}\} $
such that
$ m<\max \{\bar {u}\} $
such that
 $\mathcal {M}\models \Psi '(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar {u},m,\bar {v},m',b,a,s,\alpha ,z)$
, where
$\mathcal {M}\models \Psi '(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar {u},m,\bar {v},m',b,a,s,\alpha ,z)$
, where
 $\Psi '$
is the following
$\Psi '$
is the following
 $\Pi _{1}$
-formula:
$\Pi _{1}$
-formula:  $$ \begin{align*} \left(\begin{array}{@{}c@{}} \forall i<s(\neg[f(\bar{v},m',(a)_{i},z)\downarrow]^{<b}\rightarrow\neg[f(\bar{u},m,(a)_{i},z)\downarrow]) \ \wedge \\ \forall i<s \bigwedge_{t\leq k}\left(\begin{array}{@{}c@{}} (\langle n_{t},i\rangle\mathrm{E}\alpha'\wedge[f_{n_{t}}(\bar{u},m,(a)_{i})\downarrow]) \rightarrow \\ f_{n_{t}}(\bar{u},m,(a)_{i})\neq f_{n_{t}}(\bar{v},m',(a)_{i}) \end{array}\right)\end{array}\right). \end{align*} $$
$$ \begin{align*} \left(\begin{array}{@{}c@{}} \forall i<s(\neg[f(\bar{v},m',(a)_{i},z)\downarrow]^{<b}\rightarrow\neg[f(\bar{u},m,(a)_{i},z)\downarrow]) \ \wedge \\ \forall i<s \bigwedge_{t\leq k}\left(\begin{array}{@{}c@{}} (\langle n_{t},i\rangle\mathrm{E}\alpha'\wedge[f_{n_{t}}(\bar{u},m,(a)_{i})\downarrow]) \rightarrow \\ f_{n_{t}}(\bar{u},m,(a)_{i})\neq f_{n_{t}}(\bar{v},m',(a)_{i}) \end{array}\right)\end{array}\right). \end{align*} $$
Proof
-
(i) First note that since
 $ \mathrm {P}(\bar {u},\bar {v}) $
holds in
$ \mathrm {P}(\bar {u},\bar {v}) $
holds in
 $\mathcal {M}$
, Theorem 2.3 and Remark 1 imply that
$\mathcal {M}$
, Theorem 2.3 and Remark 1 imply that-
(1): There exists some initial self-embedding
 $ j_{0} $
of
$ j_{0} $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ j_{0}( M)<b $
,
$ j_{0}( M)<b $
,
 $ j_{0}(\bar {u})=\bar {v} $
, and
$ j_{0}(\bar {u})=\bar {v} $
, and
 $ N_{0}\subseteq \mathrm {Fix}(j_{0}) $
.
$ N_{0}\subseteq \mathrm {Fix}(j_{0}) $
.Now, suppose that part (i) of this lemma does not hold; i.e., there is some
 $ k>0 $
for which there exist
$ k>0 $
for which there exist
 $ (k+1) $
-many elements
$ (k+1) $
-many elements
 $ \lbrace f,f_{n_{1}},\ldots ,f_{n_{k}}\rbrace $
of
$ \lbrace f,f_{n_{1}},\ldots ,f_{n_{k}}\rbrace $
of
 $ \mathcal {F} $
, and some
$ \mathcal {F} $
, and some
 $ \textbf {z}\in N_{0} $
such that for all
$ \textbf {z}\in N_{0} $
such that for all
 $ s> I $
it holds that
$ s> I $
it holds that  $$ \begin{align*}\mathcal{M}\models\forall y<b \ \neg \Psi(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar{u},m,\bar{v},y,b,a,s,\alpha,\textbf{z},(a)_{\mathrm{i}}). \end{align*} $$
$$ \begin{align*}\mathcal{M}\models\forall y<b \ \neg \Psi(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar{u},m,\bar{v},y,b,a,s,\alpha,\textbf{z},(a)_{\mathrm{i}}). \end{align*} $$
Therefore, by
 $ \Sigma _{1}$
-Underspill in
$ \Sigma _{1}$
-Underspill in
 $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
 $ s\in I $
such that
$ s\in I $
such that  $$ \begin{align*}\mathcal{M}\models \forall y<b \ \neg\Psi(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar{u},m,\bar{v},y,b,a,s,\alpha,\textbf{z},(a)_{\mathrm{i}}).\end{align*} $$
$$ \begin{align*}\mathcal{M}\models \forall y<b \ \neg\Psi(f,f_{n_{1}},\ldots ,f_{n_{k}},\bar{u},m,\bar{v},y,b,a,s,\alpha,\textbf{z},(a)_{\mathrm{i}}).\end{align*} $$
-
(2): Let
 $ k_{0}\in \mathbb {N} $
be the least natural number, for which there exists a set
$ k_{0}\in \mathbb {N} $
be the least natural number, for which there exists a set
 $\lbrace f, f_{n_{1}},\ldots ,f_{n_{k_{0}}}\rbrace $
of elements of
$\lbrace f, f_{n_{1}},\ldots ,f_{n_{k_{0}}}\rbrace $
of elements of
 $ \mathcal {F} $
, some
$ \mathcal {F} $
, some
 $ \textbf {z}_{0}\in N_{0} $
, and some
$ \textbf {z}_{0}\in N_{0} $
, and some
 $ s_{0}\in I $
such that
$ s_{0}\in I $
such that  $$ \begin{align*} {\mathcal{M}\models \forall y<b \ \neg\Psi(f,f_{n_{1}},\ldots ,f_{n_{k_{0}}}, \bar{u},m,\bar{v},y,b,a,s_{0},\alpha,\textbf{z}_{0},(a)_{\mathrm{i}})}. \end{align*} $$
$$ \begin{align*} {\mathcal{M}\models \forall y<b \ \neg\Psi(f,f_{n_{1}},\ldots ,f_{n_{k_{0}}}, \bar{u},m,\bar{v},y,b,a,s_{0},\alpha,\textbf{z}_{0},(a)_{\mathrm{i}})}. \end{align*} $$
Put
By Lemma 3.3, there exist $$ \begin{align*} &\quad X:=\lbrace x\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge [f(\bar{u},m,(a)_{i}, \textbf{z}_{0})\downarrow] ) \rbrace \\ &\qquad\qquad\qquad\qquad\qquad\qquad \quad \text{and}\\ & \kern-12pt X':=\lbrace \langle n,x\rangle\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge \bigvee\nolimits_{t=1}^{\kern2pt k_{0}} n=n_{t} \wedge \langle n,i\rangle\mathrm{E}\alpha) \rbrace. \end{align*} $$
$$ \begin{align*} &\quad X:=\lbrace x\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge [f(\bar{u},m,(a)_{i}, \textbf{z}_{0})\downarrow] ) \rbrace \\ &\qquad\qquad\qquad\qquad\qquad\qquad \quad \text{and}\\ & \kern-12pt X':=\lbrace \langle n,x\rangle\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge \bigvee\nolimits_{t=1}^{\kern2pt k_{0}} n=n_{t} \wedge \langle n,i\rangle\mathrm{E}\alpha) \rbrace. \end{align*} $$
 $ (a)_{\xi }\in N_{0} $
and
$ (a)_{\xi }\in N_{0} $
and
 $ (a)_{\zeta }\in N_{0} $
which code
$ (a)_{\zeta }\in N_{0} $
which code
 $ X $
and
$ X $
and
 $ X', $
respectively. So we can restate statement (2) in the following form:
$ X', $
respectively. So we can restate statement (2) in the following form:
-
(3): Let
 $ k_{0}\in \mathbb {N} $
be the least natural number, for which there exists a set
$ k_{0}\in \mathbb {N} $
be the least natural number, for which there exists a set
 $\lbrace f, f_{n_{1}},\ldots ,f_{n_{k_{0}}}\rbrace $
of elements of
$\lbrace f, f_{n_{1}},\ldots ,f_{n_{k_{0}}}\rbrace $
of elements of
 $ \mathcal {F} $
, some
$ \mathcal {F} $
, some
 $ \textbf {z}_{0},(a)_{\zeta },(a)_{\xi }\in N_{0} $
such that Our plan is to consider two cases
$ \textbf {z}_{0},(a)_{\zeta },(a)_{\xi }\in N_{0} $
such that Our plan is to consider two cases $$ \begin{align*} \kern-40pt\mathcal{M}\models\forall y\leq t(\bar{v},(a)_{\mathrm{i}}) \left( \begin{array}{@{}c@{}} \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b} \rightarrow \\ \exists \varepsilon<\mathrm{E}(a)_{\zeta} \bigvee_{t=1}^{k_{0}} \left(\begin{array}{@{}c@{}} \langle n_{t},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \ \wedge [f_{n_{t}}(\bar{v},y,\varepsilon)\downarrow]^{<b} \wedge \\ f_{n_{t}}(\bar{u},m,\varepsilon)= f_{n_{t}}(\bar{v},y,\varepsilon) \end{array}\right) \end{array}\right).\end{align*} $$
$$ \begin{align*} \kern-40pt\mathcal{M}\models\forall y\leq t(\bar{v},(a)_{\mathrm{i}}) \left( \begin{array}{@{}c@{}} \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b} \rightarrow \\ \exists \varepsilon<\mathrm{E}(a)_{\zeta} \bigvee_{t=1}^{k_{0}} \left(\begin{array}{@{}c@{}} \langle n_{t},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \ \wedge [f_{n_{t}}(\bar{v},y,\varepsilon)\downarrow]^{<b} \wedge \\ f_{n_{t}}(\bar{u},m,\varepsilon)= f_{n_{t}}(\bar{v},y,\varepsilon) \end{array}\right) \end{array}\right).\end{align*} $$
 $ {k_{0}=1} $
and
$ {k_{0}=1} $
and
 $ {k_{0}>1} $
, and in each case obtain a contradiction. But before dividing the cases we will define some
$ {k_{0}>1} $
, and in each case obtain a contradiction. But before dividing the cases we will define some
 $ \Sigma _{1} $
-functions which will help us in achieving the desired contradictions.
$ \Sigma _{1} $
-functions which will help us in achieving the desired contradictions.
First, by considering the code of the sequence
 ${ \langle f_{n_{t}}(\bar {u},m,\varepsilon ): \, \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \rangle } $
in
${ \langle f_{n_{t}}(\bar {u},m,\varepsilon ): \, \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \rangle } $
in
 $\mathcal {M}$
, we may quantify out
$\mathcal {M}$
, we may quantify out
 $ f_{n_{t}}(\bar {u},m,\varepsilon ) $
s from the formula in statement
$ f_{n_{t}}(\bar {u},m,\varepsilon ) $
s from the formula in statement
 $ (3) $
; in other words, there exists some
$ (3) $
; in other words, there exists some
 $ \textbf {x}\in M $
such that
$ \textbf {x}\in M $
such that
 $ (\textbf {x})_{\langle n_{t},\varepsilon \rangle }=f_{n_{t}}(\bar {u},m,\varepsilon ) $
for every
$ (\textbf {x})_{\langle n_{t},\varepsilon \rangle }=f_{n_{t}}(\bar {u},m,\varepsilon ) $
for every
 $\langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } $
. So we will deduce that
$\langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } $
. So we will deduce that -
(4):
 $ \mathcal {M}\models \exists x \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \ \theta (y,b,\bar {v},x,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0}) $
, where
$ \mathcal {M}\models \exists x \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \ \theta (y,b,\bar {v},x,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0}) $
, where
 $\theta (y,b,\bar {v},x, (a)_{\xi },(a)_{\zeta },\textbf {z}_{0})$
is the following
$\theta (y,b,\bar {v},x, (a)_{\xi },(a)_{\zeta },\textbf {z}_{0})$
is the following
 $ \Delta _{0} $
-formula: Then, we will define
$ \Delta _{0} $
-formula: Then, we will define $$ \begin{align*} \left( \begin{array}{@{}c@{}} \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi} \rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b}) \rightarrow\\ \exists \langle n_{t},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \left(\begin{array}{@{}c@{}} [f_{n_{t}}(\bar{v},y,\varepsilon)\downarrow]^{<b}\wedge (x)_{\langle n_{t},\varepsilon\rangle}= f_{n_{t}}(\bar{v},y,\varepsilon) \end{array}\right)\end{array}\right). \end{align*} $$
$$ \begin{align*} \left( \begin{array}{@{}c@{}} \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi} \rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b}) \rightarrow\\ \exists \langle n_{t},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \left(\begin{array}{@{}c@{}} [f_{n_{t}}(\bar{v},y,\varepsilon)\downarrow]^{<b}\wedge (x)_{\langle n_{t},\varepsilon\rangle}= f_{n_{t}}(\bar{v},y,\varepsilon) \end{array}\right)\end{array}\right). \end{align*} $$
 $ \Sigma _{1}$
-definable partial functions
$ \Sigma _{1}$
-definable partial functions
 $ b(\diamondsuit ,y,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0}) $
and
$ b(\diamondsuit ,y,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0}) $
and
 $g(\diamondsuit ,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0},(a)_{\mathrm {i}}) $
, as follows (we omit the parameters
$g(\diamondsuit ,(a)_{\xi },(a)_{\zeta },\textbf {z}_{0},(a)_{\mathrm {i}}) $
, as follows (we omit the parameters
 $(a)_{\xi } $
,
$(a)_{\xi } $
,
 $ (a)_{\zeta } $
,
$ (a)_{\zeta } $
,
 $ (a)_{\mathrm {i}} $
, and
$ (a)_{\mathrm {i}} $
, and
 $ \textbf {z}_{0} $
in the presentations of these functions for the sake of simplicity):
$ \textbf {z}_{0} $
in the presentations of these functions for the sake of simplicity):
-
–
 $b(\diamondsuit ,y):=\min \left \lbrace w: \left (\begin{array}{@{}c@{}} \forall \epsilon \mathrm {E}(a)_{\xi } \ ([f(\diamondsuit ,y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<w})\wedge \\ \forall \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \ ([f_{n_{t}}(\diamondsuit ,y,\varepsilon )\downarrow ]^{<w}) \end {array}\right ) \right \rbrace. $
$b(\diamondsuit ,y):=\min \left \lbrace w: \left (\begin{array}{@{}c@{}} \forall \epsilon \mathrm {E}(a)_{\xi } \ ([f(\diamondsuit ,y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<w})\wedge \\ \forall \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \ ([f_{n_{t}}(\diamondsuit ,y,\varepsilon )\downarrow ]^{<w}) \end {array}\right ) \right \rbrace. $
-
–
 $ g(\diamondsuit ):=x $
iff
$ g(\diamondsuit ):=x $
iff
 $ \exists z \left (\begin{array}{@{}c@{}}(z)_{0}=x \ \wedge \\ z=\mu _{w} \ \forall y\leq t(\diamondsuit ,(a)_{\mathrm {i}}) \ \left (\begin{array}{@{}c@{}}[b(\diamondsuit ,y)\downarrow ]^{<(w)_{1}} \ \rightarrow \\ \theta (y,b(\diamondsuit ,y),\diamondsuit ,(w)_{0},(a)_{\xi },(a)_{\zeta },\textbf {z}_{0})\end {array}\right )\end {array}\right ); $
and
$ \exists z \left (\begin{array}{@{}c@{}}(z)_{0}=x \ \wedge \\ z=\mu _{w} \ \forall y\leq t(\diamondsuit ,(a)_{\mathrm {i}}) \ \left (\begin{array}{@{}c@{}}[b(\diamondsuit ,y)\downarrow ]^{<(w)_{1}} \ \rightarrow \\ \theta (y,b(\diamondsuit ,y),\diamondsuit ,(w)_{0},(a)_{\xi },(a)_{\zeta },\textbf {z}_{0})\end {array}\right )\end {array}\right ); $
and
 $ g_{t}(\diamondsuit ,\varepsilon ):=(g(\diamondsuit ))_{\langle n_{t},\varepsilon \rangle } $
, for every
$ g_{t}(\diamondsuit ,\varepsilon ):=(g(\diamondsuit ))_{\langle n_{t},\varepsilon \rangle } $
, for every
 $ \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } $
.
$ \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } $
.
From the definition of
 $ g_{t}(\bar {v},\varepsilon ) $
s and statement (4) we may infer that
$ g_{t}(\bar {v},\varepsilon ) $
s and statement (4) we may infer that -
-
(5):
 $ \mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} ([b(\bar {v},y)\downarrow ]^{<b} \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {v},y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {v},y)})) \rightarrow \\ \exists \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \left (\begin{array}{@{}c@{}} [f_{n_{t}}(\bar {v},y,\varepsilon )\downarrow ]^{<b(\bar {v},y)} \wedge [g_{t}(\bar {v},\varepsilon )\downarrow ]^{<b(\bar {v},y)} \ \wedge \\ g_{t}(\bar {v},\varepsilon )= f_{n_{t}}(\bar {v},y,\varepsilon ) \end {array}\right ) \end {array}\right )$
. It is not difficult to express the formula in the statement (5) in the form of
$ \mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} ([b(\bar {v},y)\downarrow ]^{<b} \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {v},y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {v},y)})) \rightarrow \\ \exists \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \left (\begin{array}{@{}c@{}} [f_{n_{t}}(\bar {v},y,\varepsilon )\downarrow ]^{<b(\bar {v},y)} \wedge [g_{t}(\bar {v},\varepsilon )\downarrow ]^{<b(\bar {v},y)} \ \wedge \\ g_{t}(\bar {v},\varepsilon )= f_{n_{t}}(\bar {v},y,\varepsilon ) \end {array}\right ) \end {array}\right )$
. It is not difficult to express the formula in the statement (5) in the form of
 $ {\forall z<b \ \delta (\bar {v},(a)_{\xi },(a)_{\zeta },\textbf {z}_{0})} $
for some
$ {\forall z<b \ \delta (\bar {v},(a)_{\xi },(a)_{\zeta },\textbf {z}_{0})} $
for some
 $ \Delta _{0}$
-formula
$ \Delta _{0}$
-formula
 $ \delta $
. Therefore, by the property
$ \delta $
. Therefore, by the property
 $ \mathrm {P}(\bar {u},\bar {v}) $
, the definition of function
$ \mathrm {P}(\bar {u},\bar {v}) $
, the definition of function
 $ s $
, and statement (5) we deduce that
$ s $
, and statement (5) we deduce that -
(6):
 $\mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} ([b(\bar {u},y)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {u},y)}) )\rightarrow \\ \exists \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \left (\begin{array}{@{}c@{}} [f_{n_{t}}(\bar {u},y,\varepsilon )\downarrow ]^{<b(\bar {u},y)} \wedge [g_{t}(\bar {u},\varepsilon )\downarrow ]^{<b(\bar {u},y)} ) \ \wedge \\ g_{t}(\bar {u},\varepsilon )= f_{n_{t}}(\bar {u},y,\varepsilon ) \end {array}\right )\end {array}\right )$
.
$\mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} ([b(\bar {u},y)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},y,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {u},y)}) )\rightarrow \\ \exists \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta } \left (\begin{array}{@{}c@{}} [f_{n_{t}}(\bar {u},y,\varepsilon )\downarrow ]^{<b(\bar {u},y)} \wedge [g_{t}(\bar {u},\varepsilon )\downarrow ]^{<b(\bar {u},y)} ) \ \wedge \\ g_{t}(\bar {u},\varepsilon )= f_{n_{t}}(\bar {u},y,\varepsilon ) \end {array}\right )\end {array}\right )$
.Finally, we will simultaneously define two more
 $ \Sigma _{1}$
-definable functions in
$ \Sigma _{1}$
-definable functions in
 $\mathcal {M}$
: (Note that, similar to the way we defined function g, we can express the above definition by a
$\mathcal {M}$
: (Note that, similar to the way we defined function g, we can express the above definition by a $$ \begin{align*} &\langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\\ & \quad := \min\left\lbrace\langle n_{t},\varepsilon\rangle \mathrm{E}(a)_{\zeta}: \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\wedge\\ {}[ f_{n_{t}} ({\diamondsuit}, y, {\varepsilon}){\downarrow}]^{<b({\diamondsuit},y)} \ \wedge [g_{t} ({\diamondsuit},\varepsilon) {\downarrow}]^{< b (\diamondsuit,y)} \wedge\\ g_{t}(\diamondsuit,\varepsilon)= f_{n_{t}}(\diamondsuit,y,\varepsilon)\end{array}\right) \right\rbrace. \end{align*} $$
$$ \begin{align*} &\langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\\ & \quad := \min\left\lbrace\langle n_{t},\varepsilon\rangle \mathrm{E}(a)_{\zeta}: \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\wedge\\ {}[ f_{n_{t}} ({\diamondsuit}, y, {\varepsilon}){\downarrow}]^{<b({\diamondsuit},y)} \ \wedge [g_{t} ({\diamondsuit},\varepsilon) {\downarrow}]^{< b (\diamondsuit,y)} \wedge\\ g_{t}(\diamondsuit,\varepsilon)= f_{n_{t}}(\diamondsuit,y,\varepsilon)\end{array}\right) \right\rbrace. \end{align*} $$
 $\Sigma _{1}$
-formula.) Then, by statement (5) it holds that
$\Sigma _{1}$
-formula.) Then, by statement (5) it holds that
-
(7):
 $ \mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left (\begin{array}{@{}c@{}} ([b(\bar {v},y)\downarrow ]^{<b} \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {v},y,\epsilon , \textbf {z}_{0})\downarrow ]^{<b})) \rightarrow\\ {}[\langle o(\bar {v},y),h(\bar {v},y)\rangle \downarrow ]\end {array}\right ) $
.
$ \mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left (\begin{array}{@{}c@{}} ([b(\bar {v},y)\downarrow ]^{<b} \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {v},y,\epsilon , \textbf {z}_{0})\downarrow ]^{<b})) \rightarrow\\ {}[\langle o(\bar {v},y),h(\bar {v},y)\rangle \downarrow ]\end {array}\right ) $
.Similarly, from statement (6) we may deduce that
-
(8):
 $\mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}})\left (\begin{array}{@{}c@{}} ([b(\bar {u},y)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},y,\epsilon ,\textbf {z}_{0})\downarrow]^{<b(\bar {u},y)})) \rightarrow \\ {}[\langle o(\bar {u},y),h(\bar {u},y)\rangle \downarrow] \end {array}\right ) $
.
$\mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}})\left (\begin{array}{@{}c@{}} ([b(\bar {u},y)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},y,\epsilon ,\textbf {z}_{0})\downarrow]^{<b(\bar {u},y)})) \rightarrow \\ {}[\langle o(\bar {u},y),h(\bar {u},y)\rangle \downarrow] \end {array}\right ) $
.Now, we are ready to examine the mentioned underlined cases for
 $ k_{0} $
:
$ k_{0} $
:-
– If
 $ k_{0}>1$
: By using Lemma 3.3, let
$ k_{0}>1$
: By using Lemma 3.3, let
 $ (a)_{\rho }\in N_{0} $
be the code of the following subset of
$ (a)_{\rho }\in N_{0} $
be the code of the following subset of
 $ N_{0} $
:
$ N_{0} $
:  $$ \begin{align*} \kern-56pt A:=\left\lbrace\langle o(\bar{v},y),h(\bar{v},y)\rangle: \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} y\leq t(\bar{v},(a)_{\mathrm{i}}) \wedge [\langle o(\bar{v},y),h(\bar{v},y)\rangle\downarrow]^{<b} \wedge\\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b} \wedge\\ \exists \varepsilon<(a)_{\zeta} \left(\begin{array}{@{}c@{}} \langle n_{1},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \wedge [f_{n_{1}}(\bar{v},y,\varepsilon)\downarrow]^{<b} \wedge \\ f_{n_{1}}(\bar{v},y,\varepsilon)=f_{n_{1}}(\bar{u},m,\varepsilon) \end{array}\right) \end{array}\right) \right\rbrace .\end{align*} $$
$$ \begin{align*} \kern-56pt A:=\left\lbrace\langle o(\bar{v},y),h(\bar{v},y)\rangle: \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} y\leq t(\bar{v},(a)_{\mathrm{i}}) \wedge [\langle o(\bar{v},y),h(\bar{v},y)\rangle\downarrow]^{<b} \wedge\\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\bar{v},y,\epsilon,\textbf{z}_{0})\downarrow]^{<b} \wedge\\ \exists \varepsilon<(a)_{\zeta} \left(\begin{array}{@{}c@{}} \langle n_{1},\varepsilon\rangle\mathrm{E}(a)_{\zeta} \wedge [f_{n_{1}}(\bar{v},y,\varepsilon)\downarrow]^{<b} \wedge \\ f_{n_{1}}(\bar{v},y,\varepsilon)=f_{n_{1}}(\bar{u},m,\varepsilon) \end{array}\right) \end{array}\right) \right\rbrace .\end{align*} $$
So, by statements (3), (7), and the definition of
 $ (a)_{\rho } $
, we conclude that
$ (a)_{\rho } $
, we conclude that -
-
(9):
 $\mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} \forall \epsilon <(a)_{\xi }\left ( \begin{array}{@{}c@{}} \epsilon \mathrm {E}(a)_{\xi }\rightarrow [ f(\bar {v},y,\epsilon ,\textbf {z}_{0})\downarrow]^{<b} \wedge \\ {}[\langle o(\bar {v},y),h(\bar {v},y)\rangle \downarrow]^{<b} \wedge \\ \neg \langle o(\bar {v},y),h(\bar {v},y)\rangle \mathrm {E}(a)_{\rho } \end {array}\right ) \rightarrow \\ \exists \varepsilon <\mathrm {E}(a)_{\zeta }\bigvee _{t=2}^{k_{0}} \left (\begin{array}{@{}c@{}} \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta }\wedge [f_{n_{t}}(\bar {v},y,\varepsilon )\downarrow ]^{<b}\wedge \\ f_{n_{t}}(\bar {u},m,\varepsilon )= f_{n_{t}}(\bar {v},y,\varepsilon ) \end {array}\right ) \end {array}\right )$
.
$\mathcal {M}\models \forall y\leq t(\bar {v},(a)_{\mathrm {i}}) \left ( \begin{array}{@{}c@{}} \forall \epsilon <(a)_{\xi }\left ( \begin{array}{@{}c@{}} \epsilon \mathrm {E}(a)_{\xi }\rightarrow [ f(\bar {v},y,\epsilon ,\textbf {z}_{0})\downarrow]^{<b} \wedge \\ {}[\langle o(\bar {v},y),h(\bar {v},y)\rangle \downarrow]^{<b} \wedge \\ \neg \langle o(\bar {v},y),h(\bar {v},y)\rangle \mathrm {E}(a)_{\rho } \end {array}\right ) \rightarrow \\ \exists \varepsilon <\mathrm {E}(a)_{\zeta }\bigvee _{t=2}^{k_{0}} \left (\begin{array}{@{}c@{}} \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\zeta }\wedge [f_{n_{t}}(\bar {v},y,\varepsilon )\downarrow ]^{<b}\wedge \\ f_{n_{t}}(\bar {u},m,\varepsilon )= f_{n_{t}}(\bar {v},y,\varepsilon ) \end {array}\right ) \end {array}\right )$
.Let
 $ f'\in \mathcal {F} $
such that So by considering
$ f'\in \mathcal {F} $
such that So by considering $$ \begin{align*} &\qquad\qquad f'(\diamondsuit,y,\epsilon,\langle\textbf{z}_{0},(a)_{\rho},(a)_{\zeta},(a)_{\xi}\rangle)=x \\ &\qquad\qquad\qquad\qquad\text{iff} \\ &x=f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\ \wedge [\langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\downarrow] \wedge \neg \langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\mathrm{E}(a)_{\rho}. \end{align*} $$
$$ \begin{align*} &\qquad\qquad f'(\diamondsuit,y,\epsilon,\langle\textbf{z}_{0},(a)_{\rho},(a)_{\zeta},(a)_{\xi}\rangle)=x \\ &\qquad\qquad\qquad\qquad\text{iff} \\ &x=f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\ \wedge [\langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\downarrow] \wedge \neg \langle o(\diamondsuit,y),h(\diamondsuit,y)\rangle\mathrm{E}(a)_{\rho}. \end{align*} $$
 $ f' $
instead of
$ f' $
instead of
 $ f $
in statement (3) and
$ f $
in statement (3) and
 $ \langle \textbf {z}_{0},(a)_{\rho },(a)_{\zeta },(a)_{\xi }\rangle $
instead of
$ \langle \textbf {z}_{0},(a)_{\rho },(a)_{\zeta },(a)_{\xi }\rangle $
instead of
 $ \textbf {z}_{0} $
, statement (9) leads to contradiction with the minimality of
$ \textbf {z}_{0} $
, statement (9) leads to contradiction with the minimality of
 $ k_{0} $
.
$ k_{0} $
.
-
– If
 $ k_{0}=1 $
: In this case our plan for obtaining a contradiction is as follows: on one hand, by the definitions of
$ k_{0}=1 $
: In this case our plan for obtaining a contradiction is as follows: on one hand, by the definitions of
 $ h(\bar {u},y) $
and
$ h(\bar {u},y) $
and
 $ (a)_{\zeta } $
,
$ (a)_{\zeta } $
,
 $\mathcal {M}$
thinks that the cardinality of
$\mathcal {M}$
thinks that the cardinality of
 $ \{h(\bar {u},y): \ \mathcal {M}\models (y<t(\bar {u},(a)_{\mathrm {i}})\ \wedge \ [h(\bar {u},y)\downarrow ])\} $
is at most
$ \{h(\bar {u},y): \ \mathcal {M}\models (y<t(\bar {u},(a)_{\mathrm {i}})\ \wedge \ [h(\bar {u},y)\downarrow ])\} $
is at most
 $ s_{0} $
. On the other hand, for every
$ s_{0} $
. On the other hand, for every
 $ i\in I $
we will inductively define some
$ i\in I $
we will inductively define some
 $ \Sigma _{1} $
-functions, namely
$ \Sigma _{1} $
-functions, namely
 $ w(\bar {u},i) $
s, such that
$ w(\bar {u},i) $
s, such that
 $ \mathcal {M}\models [w(\bar {u},i)\downarrow ]^{<t(\bar {u},(a)_{\mathrm {i}})} $
and
$ \mathcal {M}\models [w(\bar {u},i)\downarrow ]^{<t(\bar {u},(a)_{\mathrm {i}})} $
and
 $\mathcal {M}$
believes that there is a bijection between members of
$\mathcal {M}$
believes that there is a bijection between members of
 $ \{h(\bar {u},w(\bar {u},i)): \ i\in I \text { and } \mathcal {M}\models [h(\bar {u},w(\bar {u},i))\downarrow ]\} $
and the elements of I. So the contradiction is achieved. To be more precise, we define and
$ \{h(\bar {u},w(\bar {u},i)): \ i\in I \text { and } \mathcal {M}\models [h(\bar {u},w(\bar {u},i))\downarrow ]\} $
and the elements of I. So the contradiction is achieved. To be more precise, we define and $$ \begin{align*} \kern-56pt w(\diamondsuit,0):=\min\left\lbrace y\leq t(\diamondsuit,(a)_{\mathrm{i}}): \ \left(\begin{array}{@{}c@{}}[b(\diamondsuit,y)\downarrow]\ \wedge \ [h(\diamondsuit,y)\downarrow]^{<(a)_{\zeta}} \wedge \\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\downarrow]^{<b(\diamondsuit,y)} ) \end{array}\right) \right\rbrace, \end{align*} $$
$$ \begin{align*} \kern-56pt w(\diamondsuit,0):=\min\left\lbrace y\leq t(\diamondsuit,(a)_{\mathrm{i}}): \ \left(\begin{array}{@{}c@{}}[b(\diamondsuit,y)\downarrow]\ \wedge \ [h(\diamondsuit,y)\downarrow]^{<(a)_{\zeta}} \wedge \\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow[f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\downarrow]^{<b(\diamondsuit,y)} ) \end{array}\right) \right\rbrace, \end{align*} $$
 $w(\diamondsuit ,i+1):= \min \left \lbrace y\leq t(\diamondsuit ,(a)_{\mathrm {i}}): \varphi (\diamondsuit ,i,y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0})\right \rbrace $
, where
$w(\diamondsuit ,i+1):= \min \left \lbrace y\leq t(\diamondsuit ,(a)_{\mathrm {i}}): \varphi (\diamondsuit ,i,y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0})\right \rbrace $
, where
 $ \varphi (\diamondsuit ,i,y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0}) $
is the following formula:
$ \varphi (\diamondsuit ,i,y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0}) $
is the following formula:  $$ \begin{align*} \kern-24pt \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\ \wedge [h(\diamondsuit,y)\downarrow]^{<(a)_{\zeta}} \wedge \\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow [f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\downarrow]^{<b(\diamondsuit,y)}) \ \wedge \\ \forall x\leq i \left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}} [h(\diamondsuit,w(\diamondsuit,x))\downarrow]^{<(a)_{\zeta}}\wedge\\ {}[f_{n_{1}}(\diamondsuit,y,h(\diamondsuit,w(\diamondsuit,x)))\downarrow]^{<b(\diamondsuit,y)}\wedge\\ {}[f_{n_{1}}(\diamondsuit,w(\diamondsuit,x),h(\diamondsuit,w(\diamondsuit,x)))\downarrow]^{<b(\diamondsuit,w(\diamondsuit,x))}\end{array}\right) \rightarrow \\ f_{n_{1}}(\diamondsuit,y,h(\diamondsuit,w(\diamondsuit,x)))\neq f_{n_{1}}(\diamondsuit,w(\diamondsuit,x),h(\diamondsuit,w(\diamondsuit,x))) \end{array}\right)\end{array}\right). \end{align*} $$
$$ \begin{align*} \kern-24pt \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\ \wedge [h(\diamondsuit,y)\downarrow]^{<(a)_{\zeta}} \wedge \\ \forall \epsilon<(a)_{\xi}( \epsilon\mathrm{E}(a)_{\xi}\rightarrow [f(\diamondsuit,y,\epsilon,\textbf{z}_{0})\downarrow]^{<b(\diamondsuit,y)}) \ \wedge \\ \forall x\leq i \left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}} [h(\diamondsuit,w(\diamondsuit,x))\downarrow]^{<(a)_{\zeta}}\wedge\\ {}[f_{n_{1}}(\diamondsuit,y,h(\diamondsuit,w(\diamondsuit,x)))\downarrow]^{<b(\diamondsuit,y)}\wedge\\ {}[f_{n_{1}}(\diamondsuit,w(\diamondsuit,x),h(\diamondsuit,w(\diamondsuit,x)))\downarrow]^{<b(\diamondsuit,w(\diamondsuit,x))}\end{array}\right) \rightarrow \\ f_{n_{1}}(\diamondsuit,y,h(\diamondsuit,w(\diamondsuit,x)))\neq f_{n_{1}}(\diamondsuit,w(\diamondsuit,x),h(\diamondsuit,w(\diamondsuit,x))) \end{array}\right)\end{array}\right). \end{align*} $$
First, we will show that
 $ \mathcal {M}\models [w(\bar {u},i)\downarrow ] $
for all
$ \mathcal {M}\models [w(\bar {u},i)\downarrow ] $
for all
 $ i\in I $
. Otherwise, there exists the least
$ i\in I $
. Otherwise, there exists the least
 $ 0<i_{0}\in I $
such that
$ 0<i_{0}\in I $
such that -
-
(10):
 $ \mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}}) \ \neg \varphi (\bar {u},i_{0},y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0})$
.
$ \mathcal {M}\models \forall y\leq t(\bar {u},(a)_{\mathrm {i}}) \ \neg \varphi (\bar {u},i_{0},y,(a)_{\zeta },(a)_{\xi },\textbf {z}_{0})$
.Note that by the definition of
 $ (a)_{\xi } $
and
$ (a)_{\xi } $
and
 $ (a)_{\zeta } $
it holds that
$ (a)_{\zeta } $
it holds that -
(11):
 $\mathcal {M}\models ([b(\bar {u},m)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},m,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {u},m)}) $
.
$\mathcal {M}\models ([b(\bar {u},m)\downarrow ] \ \wedge \ \forall \epsilon <(a)_{\xi }( \epsilon \mathrm {E}(a)_{\xi }\rightarrow [f(\bar {u},m,\epsilon ,\textbf {z}_{0})\downarrow ]^{<b(\bar {u},m)}) $
.So by statements (8), (10), and (11), there exists some
 $ i_{1}< i_{0} $
such that
$ i_{1}< i_{0} $
such that -
(12):
 $\mathcal {M}\models \left (\begin{array}{@{}c@{}} [h(\bar {u},w(\bar {u},i_{1}))\downarrow] \wedge [f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u},i_{1})))\downarrow] \wedge \\ {}[f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1})))\downarrow] \wedge \\ f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u}, i_{1})))= f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1}))) \end {array}\right ) $
.
$\mathcal {M}\models \left (\begin{array}{@{}c@{}} [h(\bar {u},w(\bar {u},i_{1}))\downarrow] \wedge [f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u},i_{1})))\downarrow] \wedge \\ {}[f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1})))\downarrow] \wedge \\ f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u}, i_{1})))= f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1}))) \end {array}\right ) $
.Clearly,
 $f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1})))\in \mathrm {K}^{1}(\mathcal {M};N_{0}\cup \{\bar {u}\}) $
. So by statement (12),
$f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{1})))\in \mathrm {K}^{1}(\mathcal {M};N_{0}\cup \{\bar {u}\}) $
. So by statement (12),
 $f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u},i_{1}))) \in \mathrm {K}^{1}(\mathcal {M};M_{0}\cup \{\bar {u}\}) $
. So
$f_{n_{1}}(\bar {u},m,h(\bar {u},w(\bar {u},i_{1}))) \in \mathrm {K}^{1}(\mathcal {M};M_{0}\cup \{\bar {u}\}) $
. So
 $ \mathcal {M}\models \neg \langle n_{1},h(\bar {u},w(\bar {u},i_{1}))\rangle \mathrm {E}(a)_{\zeta } $
(by the definition of
$ \mathcal {M}\models \neg \langle n_{1},h(\bar {u},w(\bar {u},i_{1}))\rangle \mathrm {E}(a)_{\zeta } $
(by the definition of
 $ (a)_{\zeta } $
), which is in contradiction with the definition of the function
$ (a)_{\zeta } $
), which is in contradiction with the definition of the function
 $ h $
.
$ h $
.Then, by the definition of
 $ w(\bar {u},i) $
s and statement (8), the function
$ w(\bar {u},i) $
s and statement (8), the function
 $ {i\mapsto h(\bar {u},w(\bar {u},i))} $
from
$ {i\mapsto h(\bar {u},w(\bar {u},i))} $
from
 $\{i: \ i\leq s_{0}+1\} $
into
$\{i: \ i\leq s_{0}+1\} $
into
 $ ((a)_{\zeta })_{\mathrm {E}} $
is well-defined and coded in
$ ((a)_{\zeta })_{\mathrm {E}} $
is well-defined and coded in
 $\mathcal {M}$
. So, since the cardinality of
$\mathcal {M}$
. So, since the cardinality of
 $ (a)_{\zeta } $
is less than
$ (a)_{\zeta } $
is less than
 $ s_{0}+1 $
, by
$ s_{0}+1 $
, by
 $ \Sigma _{1}$
-Pigeonhole Principle in
$ \Sigma _{1}$
-Pigeonhole Principle in
 $\mathcal {M}$
, there exists some distinct
$\mathcal {M}$
, there exists some distinct
 $ i_{0}<i_{1}\leq s_{0}+1 $
such that
$ i_{0}<i_{1}\leq s_{0}+1 $
such that -
(13):
 $\mathcal {M}\models h(\bar {u},w(\bar {u},i_{0}))=h(\bar {u},w(\bar {u},i_{1}))$
.
$\mathcal {M}\models h(\bar {u},w(\bar {u},i_{0}))=h(\bar {u},w(\bar {u},i_{1}))$
.Therefore, by statement (13) and the definition of
 $ h $
we conclude that
$ h $
we conclude that -
(14):
 $ \mathcal {M}\models \left (\begin{array}{@{}c@{}} [g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{0})))\downarrow ] \wedge [g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{1})))\downarrow ]\wedge \\ g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{0})))=g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{1}))) \end {array}\right ) $
.
$ \mathcal {M}\models \left (\begin{array}{@{}c@{}} [g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{0})))\downarrow ] \wedge [g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{1})))\downarrow ]\wedge \\ g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{0})))=g_{1}(\bar {u},h(\bar {u},w(\bar {u},i_{1}))) \end {array}\right ) $
.Moreover, by the definition of
 $ h(\bar {u},w(\bar {u},i)) $
, for
$ h(\bar {u},w(\bar {u},i)) $
, for
 $ i=i_{0},i_{1} $
it holds that
$ i=i_{0},i_{1} $
it holds that -
(15):
 $\mathcal {M}\models \left (\begin{array}{@{}c@{}} [f_{n_{1}}(\bar {u},w(\bar {u},i),h(\bar {u},w(\bar {u},i)))\downarrow ] \ \wedge [g_{1}(\bar {u},h(\bar {u},w(\bar {u})))\downarrow ] \wedge \\ f_{n_{1}}(\bar {u},w(\bar {u},i),h(\bar {u},w(\bar {u},i)))=g_{1}(\bar {u},h(\bar {u},w(\bar {u}))) \end {array}\right )$
.
$\mathcal {M}\models \left (\begin{array}{@{}c@{}} [f_{n_{1}}(\bar {u},w(\bar {u},i),h(\bar {u},w(\bar {u},i)))\downarrow ] \ \wedge [g_{1}(\bar {u},h(\bar {u},w(\bar {u})))\downarrow ] \wedge \\ f_{n_{1}}(\bar {u},w(\bar {u},i),h(\bar {u},w(\bar {u},i)))=g_{1}(\bar {u},h(\bar {u},w(\bar {u}))) \end {array}\right )$
.So statements (13–15) imply that
-
(16):
 $\mathcal {M}\models f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{0})))=f_{n_{1}}(\bar {u}, w(\bar {u},i_{0}),h(\bar {u},w(\bar {u},i_{0}))) $
.
$\mathcal {M}\models f_{n_{1}}(\bar {u},w(\bar {u},i_{1}),h(\bar {u},w(\bar {u},i_{0})))=f_{n_{1}}(\bar {u}, w(\bar {u},i_{0}),h(\bar {u},w(\bar {u},i_{0}))) $
.But statement (16) is in contradiction with the definition of
 $ w(\bar {u},i_{1}) $
.
$ w(\bar {u},i_{1}) $
. -
(ii) Part (ii) of this lemma will be proved exactly like part (i), except we need an extra statement between statements (3) and (4): by using
 $ \Sigma _{1}$
-Collection, we deduce that
$ \Sigma _{1}$
-Collection, we deduce that -
(3’):
 $\mathcal {M}\models \exists w \forall x<u_{0} \left (\begin{array}{@{}c@{}} \forall \epsilon <(a)_{\lambda } \ ([f(\bar {u},x,\epsilon ,\textbf {z}_{0})\downarrow ]^{<w}\rightarrow \epsilon \mathrm {E}(a)_{\lambda })\rightarrow \\ \exists \varepsilon <(a)_{\eta } \bigvee _{t\leq k_{1}}\left (\begin{array}{@{}c@{}} \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\eta }\wedge [f_{n_{t}}(\bar {u},x,\varepsilon )\downarrow ]^{<w}\wedge \\ f_{n_{t}}(\bar {u},x,\varepsilon )= f_{n_{t}}(\bar {v},m',\varepsilon ) \end {array}\right ) \end {array}\right ) $
;
$\mathcal {M}\models \exists w \forall x<u_{0} \left (\begin{array}{@{}c@{}} \forall \epsilon <(a)_{\lambda } \ ([f(\bar {u},x,\epsilon ,\textbf {z}_{0})\downarrow ]^{<w}\rightarrow \epsilon \mathrm {E}(a)_{\lambda })\rightarrow \\ \exists \varepsilon <(a)_{\eta } \bigvee _{t\leq k_{1}}\left (\begin{array}{@{}c@{}} \langle n_{t},\varepsilon \rangle \mathrm {E}(a)_{\eta }\wedge [f_{n_{t}}(\bar {u},x,\varepsilon )\downarrow ]^{<w}\wedge \\ f_{n_{t}}(\bar {u},x,\varepsilon )= f_{n_{t}}(\bar {v},m',\varepsilon ) \end {array}\right ) \end {array}\right ) $
;in which
 $(a)_{\lambda }\in N_{0} $
and
$(a)_{\lambda }\in N_{0} $
and
 $ (a)_{\eta }\in N_{0} $
code the following Y and
$ (a)_{\eta }\in N_{0} $
code the following Y and
 $Y',$
respectively:
$Y',$
respectively:  $$ \begin{align*} &Y:=\lbrace x\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge[f(\bar{v},m',(a)_{i},\textbf{z}_{0})\downarrow]^{<b} ) \rbrace, \text{ and } \\ &Y':=\lbrace \langle n,x\rangle\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge \bigvee_{t=0}^{k_{0}}n=n_{t} \wedge \langle n,i\rangle\mathrm{E}\alpha') \rbrace. \end{align*} $$
$$ \begin{align*} &Y:=\lbrace x\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge[f(\bar{v},m',(a)_{i},\textbf{z}_{0})\downarrow]^{<b} ) \rbrace, \text{ and } \\ &Y':=\lbrace \langle n,x\rangle\in M: \ \mathcal{M}\models\exists i<s_{0}(x=(a)_{i}\wedge \bigvee_{t=0}^{k_{0}}n=n_{t} \wedge \langle n,i\rangle\mathrm{E}\alpha') \rbrace. \end{align*} $$
-
Now we are ready to prove Theorem 3.4.
Proof of Theorem 3.4
By Lemma 3.4.1, there exists some
![]() $ a\in M $
such that
$ a\in M $
such that
![]() $ {N_{0}=\{(a)_{i}: i\in I\}} $
and
$ {N_{0}=\{(a)_{i}: i\in I\}} $
and
![]() $ (a)_{i}\neq (a)_{i} $
for distinct
$ (a)_{i}\neq (a)_{i} $
for distinct
![]() $ i,j\in I $
. Now, in order to construct
$ i,j\in I $
. Now, in order to construct
![]() $ j $
, first by using strong
$ j $
, first by using strong
![]() $ \Sigma _{1}$
-Collection in
$ \Sigma _{1}$
-Collection in
![]() $\mathcal {M}$
, we will find some
$\mathcal {M}$
, we will find some
![]() $ b\in M $
such that
$ b\in M $
such that
Then, by using back-and-forth method we will inductively build finite functions
![]() $\bar {u}\mapsto \bar {v}$
such that
$\bar {u}\mapsto \bar {v}$
such that
![]() $ \bar {u},\bar {v}\in M $
, and
$ \bar {u},\bar {v}\in M $
, and
![]() $\mathcal {M}\models (\bar {v}<b \ \wedge \ \mathrm {P}(\bar {u},\bar {v}) \ \wedge \mathrm {Q}(\bar {u},\bar {v}) )$
, where
$\mathcal {M}\models (\bar {v}<b \ \wedge \ \mathrm {P}(\bar {u},\bar {v}) \ \wedge \mathrm {Q}(\bar {u},\bar {v}) )$
, where
![]() $ \mathrm {P}(\bar {u},\bar {v}) $
and
$ \mathrm {P}(\bar {u},\bar {v}) $
and
![]() $ \mathrm {Q}(\bar {u},\bar {v}) $
are properties as stated in Lemma 3.4.3. Through the “forth” stages of back-and-forth we shall make the domain of
$ \mathrm {Q}(\bar {u},\bar {v}) $
are properties as stated in Lemma 3.4.3. Through the “forth” stages of back-and-forth we shall make the domain of
![]() $ j $
to be equal to
$ j $
to be equal to
![]() $ M $
, and “back” stages are for making the range of
$ M $
, and “back” stages are for making the range of
![]() $ j $
to be an initial segment of
$ j $
to be an initial segment of
![]() $\mathcal {M}$
. For the first step of induction, we will choose
$\mathcal {M}$
. For the first step of induction, we will choose
![]() $0\mapsto 0 $
. Then, suppose
$0\mapsto 0 $
. Then, suppose
![]() $\bar {u}\mapsto \bar {v}$
is built such that
$\bar {u}\mapsto \bar {v}$
is built such that
![]() $\mathcal {M}\models (\bar {v}<b \ \wedge \ \mathrm {P}(\bar {u},\bar {v}) \ \wedge \mathrm {Q}(\bar {u},\bar {v}) )$
.
$\mathcal {M}\models (\bar {v}<b \ \wedge \ \mathrm {P}(\bar {u},\bar {v}) \ \wedge \mathrm {Q}(\bar {u},\bar {v}) )$
.
“Forth” stages: Let
![]() $ m\in M\setminus \{\bar {u}\} $
be arbitrary. By the definition of
$ m\in M\setminus \{\bar {u}\} $
be arbitrary. By the definition of
![]() $\mathcal {M}$
, without loss of generality, we can assume that
$\mathcal {M}$
, without loss of generality, we can assume that
![]() $ m\leq t(\bar {u},(a)_{\mathrm {i}}) $
for some
$ m\leq t(\bar {u},(a)_{\mathrm {i}}) $
for some
![]() $ t\in \mathcal {F} $
and
$ t\in \mathcal {F} $
and
![]() $ \mathrm {i}\in I $
. Moreover, let
$ \mathrm {i}\in I $
. Moreover, let
![]() $ \alpha \in M $
be as in Lemma 3.4.2. In order to find some image for
$ \alpha \in M $
be as in Lemma 3.4.2. In order to find some image for
![]() $ m $
, for every
$ m $
, for every
![]() $ s\in M $
we define the following bounded
$ s\in M $
we define the following bounded
![]() $ \Pi _{1} $
-type:
$ \Pi _{1} $
-type:
 $$ \begin{align*} &\qquad p_{s}(y):= \lbrace y\leq t(\bar{v},(a)_{\mathrm{i}})\rbrace\cup p_{s1}(y)\cup p_{s2}(y), \text{where} \\ &\quad {p_{s1}(y):=\lbrace\forall i<s([f(\bar{u},m,(a)_{i})\downarrow]\rightarrow [f(\bar{v},y,(a)_{i})\downarrow]^{<b}): f\in\mathcal{F}\rbrace;} \\ &\qquad\qquad\qquad\qquad\qquad\text{and} \\ &p_{s2}(y):=\left\lbrace \forall i<s \left(\begin{array}{@{}c@{}} ([f_{n}(\bar{v},y,(a)_{i})\downarrow]^{<b} \wedge\langle n,i\rangle\mathrm{E}\alpha)\rightarrow \\ f_{n}(\bar{u},m,(a)_{i})\neq f_{n}(\bar{v},y,(a)_{i})\end{array}\right): \ n\in\mathbb{N} \right\rbrace. \end{align*} $$
$$ \begin{align*} &\qquad p_{s}(y):= \lbrace y\leq t(\bar{v},(a)_{\mathrm{i}})\rbrace\cup p_{s1}(y)\cup p_{s2}(y), \text{where} \\ &\quad {p_{s1}(y):=\lbrace\forall i<s([f(\bar{u},m,(a)_{i})\downarrow]\rightarrow [f(\bar{v},y,(a)_{i})\downarrow]^{<b}): f\in\mathcal{F}\rbrace;} \\ &\qquad\qquad\qquad\qquad\qquad\text{and} \\ &p_{s2}(y):=\left\lbrace \forall i<s \left(\begin{array}{@{}c@{}} ([f_{n}(\bar{v},y,(a)_{i})\downarrow]^{<b} \wedge\langle n,i\rangle\mathrm{E}\alpha)\rightarrow \\ f_{n}(\bar{u},m,(a)_{i})\neq f_{n}(\bar{v},y,(a)_{i})\end{array}\right): \ n\in\mathbb{N} \right\rbrace. \end{align*} $$
We claim that there exists some
![]() $ s> I $
such that the type
$ s> I $
such that the type
![]() $ p_{s}(y) $
is finitely satisfiable in
$ p_{s}(y) $
is finitely satisfiable in
![]() $\mathcal {M}$
. Then since
$\mathcal {M}$
. Then since
![]() $ p_{s} $
is a
$ p_{s} $
is a
![]() $ \Pi _{1} $
, bounded and recursive type in
$ \Pi _{1} $
, bounded and recursive type in
![]() $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
![]() $ m' $
which realizes
$ m' $
which realizes
![]() $ p_{s}(y) $
in
$ p_{s}(y) $
in
![]() $\mathcal {M}$
. Therefore,
$\mathcal {M}$
. Therefore,
![]() $\mathrm {P}((\bar {u},m),(\bar {v},m')) $
and
$\mathrm {P}((\bar {u},m),(\bar {v},m')) $
and
![]() $ \mathrm {Q}((\bar {u},m),(\bar {v},m')) $
hold in
$ \mathrm {Q}((\bar {u},m),(\bar {v},m')) $
hold in
![]() $\mathcal {M}$
, and this finishes the “forth” stage.
$\mathcal {M}$
, and this finishes the “forth” stage.
In order to prove the above claim, let
![]() $ d> I $
be an arbitrary and fixed element of
$ d> I $
be an arbitrary and fixed element of
![]() $ M $
. Moreover, suppose
$ M $
. Moreover, suppose
![]() $i,s\in M$
, and
$i,s\in M$
, and
![]() $ \Theta (s,i,\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}}) $
is the following
$ \Theta (s,i,\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}}) $
is the following
![]() $ \Delta _{0}$
-formula:
$ \Delta _{0}$
-formula:
 $$ \begin{align*} {\forall r<i \ \exists y\leq t(\bar{v},(a)_{\mathrm{i}}) \left(\begin{array}{@{}c@{}} \forall w<s (\langle r,w\rangle\mathrm{E}\beta\rightarrow [f_{r}(\bar{v},y,(a)_{w})\downarrow]^{<b}) \ \wedge \\ \forall w<s \forall r'<i\left(\begin{array}{@{}c@{}} ([f_{r'}(\bar{v},y,(a)_{w})\downarrow]^{<b}\wedge \langle r',w\rangle\mathrm{E}\alpha)\rightarrow \\ f_{r'}(\bar{u},m,(a)_{w})\neq f_{r'}(\bar{v},y,(a)_{w}) \end{array}\right) \end{array}\right) }, \end{align*} $$
$$ \begin{align*} {\forall r<i \ \exists y\leq t(\bar{v},(a)_{\mathrm{i}}) \left(\begin{array}{@{}c@{}} \forall w<s (\langle r,w\rangle\mathrm{E}\beta\rightarrow [f_{r}(\bar{v},y,(a)_{w})\downarrow]^{<b}) \ \wedge \\ \forall w<s \forall r'<i\left(\begin{array}{@{}c@{}} ([f_{r'}(\bar{v},y,(a)_{w})\downarrow]^{<b}\wedge \langle r',w\rangle\mathrm{E}\alpha)\rightarrow \\ f_{r'}(\bar{u},m,(a)_{w})\neq f_{r'}(\bar{v},y,(a)_{w}) \end{array}\right) \end{array}\right) }, \end{align*} $$
where
![]() $ \beta $
is the code of the following
$ \beta $
is the code of the following
![]() $ \Sigma _{1}$
-definable set in
$ \Sigma _{1}$
-definable set in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
Note that the parameter
![]() $ i $
in
$ i $
in
![]() $ \Theta $
is for bounding indexes of functions which appear in
$ \Theta $
is for bounding indexes of functions which appear in
![]() $ \Theta $
. Moreover, the parameter
$ \Theta $
. Moreover, the parameter
![]() $ s $
is for bounding elements of
$ s $
is for bounding elements of
![]() $ N_{0} $
appearing in
$ N_{0} $
appearing in
![]() $ \Theta $
; i.e., if
$ \Theta $
; i.e., if
![]() $ \Theta $
contains some element of the form
$ \Theta $
contains some element of the form
![]() $ (a)_{w} $
, then
$ (a)_{w} $
, then
![]() $ w<s $
. Now, for every
$ w<s $
. Now, for every
![]() $ i\in M $
, we let
$ i\in M $
, we let
![]() $\mathrm {G}(i) $
be an upper bound for parameters
$\mathrm {G}(i) $
be an upper bound for parameters
![]() $ s $
as above. To be more precise, we define
$ s $
as above. To be more precise, we define
Clearly
![]() $ \mathrm {G} $
is
$ \mathrm {G} $
is
![]() $ \Delta _{0}$
-definable function in
$ \Delta _{0}$
-definable function in
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ I\subseteq \mathrm {Dom}(\mathrm {G}) $
(we assume
$ I\subseteq \mathrm {Dom}(\mathrm {G}) $
(we assume
![]() $ \mathrm {max}(\emptyset )=0 $
). Therefore, since
$ \mathrm {max}(\emptyset )=0 $
). Therefore, since
![]() $ I $
is strong, there exists some
$ I $
is strong, there exists some
![]() $ e> I $
such that for all
$ e> I $
such that for all
![]() $ i\in I $
,
$ i\in I $
,
![]() $ \mathrm {G}(i)> I $
iff
$ \mathrm {G}(i)> I $
iff
![]() $ \mathrm {G}(i)>e $
. We will show that
$ \mathrm {G}(i)>e $
. We will show that
![]() $ p_{e}(y) $
is finitely satisfiable in
$ p_{e}(y) $
is finitely satisfiable in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
First, note that,
![]() $ p_{e1}(y) $
is closed under conjunctions. (This holds similar to the way statement (1) in the proof of Lemma 3.4.3 holds.) So let
$ p_{e1}(y) $
is closed under conjunctions. (This holds similar to the way statement (1) in the proof of Lemma 3.4.3 holds.) So let
![]() $f_{n}, f_{n_{1}},\ldots ,f_{n_{k}} $
be some finite number of elements of
$f_{n}, f_{n_{1}},\ldots ,f_{n_{k}} $
be some finite number of elements of
![]() $ \mathcal {F} $
, and let
$ \mathcal {F} $
, and let
![]() $ n^{*}=\mathrm {max}\lbrace n,n_{0},\ldots ,n_{k}\rbrace $
. Then, use Lemma 3.4.3(i),
$ n^{*}=\mathrm {max}\lbrace n,n_{0},\ldots ,n_{k}\rbrace $
. Then, use Lemma 3.4.3(i),
![]() $ (n^{*}+2)$
-many times; i.e., for every
$ (n^{*}+2)$
-many times; i.e., for every
![]() $ t=0,\ldots ,n^{*}+1 $
consider
$ t=0,\ldots ,n^{*}+1 $
consider
![]() $ f_{t} $
instead of
$ f_{t} $
instead of
![]() $ f $
in the assertion of Lemma 3.4.3(i),
$ f $
in the assertion of Lemma 3.4.3(i),
![]() $ 0\in M_{0} $
instead of
$ 0\in M_{0} $
instead of
![]() $ z $
, and
$ z $
, and
![]() $ f_{1},\ldots ,f_{n^{*}} $
. So by Lemma 3.4.3(i), for every
$ f_{1},\ldots ,f_{n^{*}} $
. So by Lemma 3.4.3(i), for every
![]() $ t=0,\ldots ,n^{*}+1 $
there exists some
$ t=0,\ldots ,n^{*}+1 $
there exists some
![]() $ s_{t}> I $
such that
$ s_{t}> I $
such that
-
(1):
 $ \mathcal {M}\models \exists y<b\ \Psi (f_{t},f_{1},\ldots ,f_{n^{*}}, \bar {u},m,\bar {v},y,b,a,s_{t},\alpha ,0,(a)_{\mathrm {i}}) $
.
$ \mathcal {M}\models \exists y<b\ \Psi (f_{t},f_{1},\ldots ,f_{n^{*}}, \bar {u},m,\bar {v},y,b,a,s_{t},\alpha ,0,(a)_{\mathrm {i}}) $
.Then, let
 $ s^{*}:=\mathrm {min}\lbrace s_{t}: \ t<n^{*}+1\rbrace $
. Therefore, by statement (1) and the definitions of
$ s^{*}:=\mathrm {min}\lbrace s_{t}: \ t<n^{*}+1\rbrace $
. Therefore, by statement (1) and the definitions of
 $ \Theta $
and
$ \Theta $
and
 $ \Psi $
it holds that
$ \Psi $
it holds that -
(2):
 $ {\mathcal {M}\models \Theta (s^{*},n^{*},\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})} $
.
$ {\mathcal {M}\models \Theta (s^{*},n^{*},\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})} $
.So from statement (2) and the definition of
 $ \mathrm {G} $
, we infer that
$ \mathrm {G} $
, we infer that
 $ \mathrm {G}(n^{*})>I$
and it holds that
$ \mathrm {G}(n^{*})>I$
and it holds that -
(3):
 $ {\mathcal {M}\models \Theta (\mathrm {G}(n^{*}),n^{*}, \bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})} $
.
$ {\mathcal {M}\models \Theta (\mathrm {G}(n^{*}),n^{*}, \bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})} $
.Consequently
 $ \mathrm {G}(n^{*})>e $
, and again by the definition of
$ \mathrm {G}(n^{*})>e $
, and again by the definition of
 $ \Theta $
and statement (3), we deduce that
$ \Theta $
and statement (3), we deduce that -
(4):
 $\mathcal {M}\models \Theta (e,n^{*},\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})$
.
$\mathcal {M}\models \Theta (e,n^{*},\bar {u},m,\bar {v},b,a,\alpha ,\beta ,(a)_{\mathrm {i}})$
.Statement (4) implies that
-
(4):
 $ \mathcal {M}\models \exists y\leq t(\bar {v},(a)_{\mathrm {i}}) \left (\begin{array}{@{}c@{}} \forall i<e ([f_{n}(\bar {u},m,(a)_{i})\downarrow ]\rightarrow [f_{n}(\bar {v},y,(a)_{i})\downarrow ]^{<b}) \ \wedge \\ \bigwedge _{t= 1}^{k}\forall i<e \left (\begin{array}{@{}c@{}} ([f_{n_{t}}(\bar {v},y,(a)_{i})\downarrow ]^{<b}\wedge \langle n_{t},i\rangle \mathrm {E}\alpha )\rightarrow \\ f_{n_{t}}(\bar {u},m,(a)_{i})\neq f_{n_{t}}(\bar {v},y,(a)_{i}) \end {array}\right ) \end {array}\right ) $
.
$ \mathcal {M}\models \exists y\leq t(\bar {v},(a)_{\mathrm {i}}) \left (\begin{array}{@{}c@{}} \forall i<e ([f_{n}(\bar {u},m,(a)_{i})\downarrow ]\rightarrow [f_{n}(\bar {v},y,(a)_{i})\downarrow ]^{<b}) \ \wedge \\ \bigwedge _{t= 1}^{k}\forall i<e \left (\begin{array}{@{}c@{}} ([f_{n_{t}}(\bar {v},y,(a)_{i})\downarrow ]^{<b}\wedge \langle n_{t},i\rangle \mathrm {E}\alpha )\rightarrow \\ f_{n_{t}}(\bar {u},m,(a)_{i})\neq f_{n_{t}}(\bar {v},y,(a)_{i}) \end {array}\right ) \end {array}\right ) $
.
So statement (4) finishes the proof of the claim.
“Back” stages: Let
![]() $ m'\in M\setminus \{\bar {v}\} $
such that
$ m'\in M\setminus \{\bar {v}\} $
such that
![]() $ m'<v_{0}:=\max \{\bar {v}\} $
, and
$ m'<v_{0}:=\max \{\bar {v}\} $
, and
![]() $ u_{0}:=\max \{\bar {u}\} $
. In order to find some element of
$ u_{0}:=\max \{\bar {u}\} $
. In order to find some element of
![]() $ M $
whose image is
$ M $
whose image is
![]() $ m' $
, we modify the proof of the “forth” stage in the following way:
$ m' $
, we modify the proof of the “forth” stage in the following way:
-
• Replace
 $ p_{s}(y) $
by
$ p_{s}(y) $
by  $$ \begin{align*} &\qquad\qquad\qquad q_{s}(x):= \lbrace x<u_{0}\rbrace\cup q_{s1}(x)\cup q_{s2}(x) , \text{where,} \\ &{q_{s1}(x):= \lbrace\forall i<s(\neg [f(\bar{v},m', (a)_{i})\downarrow]^{<b}\rightarrow\neg [f(\bar{u},x,(a)_{i})\downarrow] ): f\in\mathcal{F}\rbrace;} \text{ and}\\ &\qquad {q_{s2}(x):=\left\lbrace\begin{array}{@{}c@{}} \forall i<s\left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle n,i\rangle\mathrm{E}\alpha'\wedge\\ {}[f_{n}(\bar{u},x,(a)_{i})\downarrow]\end{array}\right)\rightarrow \\ f_{n}(\bar{u},x,(a)_{i})\neq f_{n}(\bar{v},m',(a)_{i}) \end{array}\right): \ n\in\mathbb{N} \end{array}\right\rbrace}. \end{align*} $$
$$ \begin{align*} &\qquad\qquad\qquad q_{s}(x):= \lbrace x<u_{0}\rbrace\cup q_{s1}(x)\cup q_{s2}(x) , \text{where,} \\ &{q_{s1}(x):= \lbrace\forall i<s(\neg [f(\bar{v},m', (a)_{i})\downarrow]^{<b}\rightarrow\neg [f(\bar{u},x,(a)_{i})\downarrow] ): f\in\mathcal{F}\rbrace;} \text{ and}\\ &\qquad {q_{s2}(x):=\left\lbrace\begin{array}{@{}c@{}} \forall i<s\left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle n,i\rangle\mathrm{E}\alpha'\wedge\\ {}[f_{n}(\bar{u},x,(a)_{i})\downarrow]\end{array}\right)\rightarrow \\ f_{n}(\bar{u},x,(a)_{i})\neq f_{n}(\bar{v},m',(a)_{i}) \end{array}\right): \ n\in\mathbb{N} \end{array}\right\rbrace}. \end{align*} $$
-
• Replace
 $ \Theta (s,i,\bar {u},m,\bar {v},b,a,\alpha ,\beta ) $
with
$ \Theta (s,i,\bar {u},m,\bar {v},b,a,\alpha ,\beta ) $
with
 $ \Theta '(s,i,\bar {u},\bar {v},m',b,a,\alpha ',\beta ') $
: where
$ \Theta '(s,i,\bar {u},\bar {v},m',b,a,\alpha ',\beta ') $
: where $$ \begin{align*} \forall r<i \ \exists x<u_{0}\left(\begin{array}{@{}c@{}} \forall w<s(\langle x,r,w\rangle\mathrm{E}\beta'\rightarrow[f_{r}(\bar{v},m',(a)_{w})\downarrow]^{<b})\wedge \\ \forall w<s \forall r'<i \left(\begin{array}{@{}c@{}} (\langle r',w\rangle\mathrm{E}\alpha'\wedge\langle x,r',w\rangle\mathrm{E}\beta')\rightarrow\\ f_{r'}(\bar{u},m,(a)_{w})\neq f_{r'}(\bar{v},y,(a)_{w}))\end{array}\right) \end{array}\right),\end{align*} $$
$$ \begin{align*} \forall r<i \ \exists x<u_{0}\left(\begin{array}{@{}c@{}} \forall w<s(\langle x,r,w\rangle\mathrm{E}\beta'\rightarrow[f_{r}(\bar{v},m',(a)_{w})\downarrow]^{<b})\wedge \\ \forall w<s \forall r'<i \left(\begin{array}{@{}c@{}} (\langle r',w\rangle\mathrm{E}\alpha'\wedge\langle x,r',w\rangle\mathrm{E}\beta')\rightarrow\\ f_{r'}(\bar{u},m,(a)_{w})\neq f_{r'}(\bar{v},y,(a)_{w}))\end{array}\right) \end{array}\right),\end{align*} $$
 $ \beta ' $
is the code of the following
$ \beta ' $
is the code of the following
 $ \Sigma _{1}$
-definable set in
$ \Sigma _{1}$
-definable set in
 $\mathcal {M}$
:
$\mathcal {M}$
:  $$ \begin{align*} L':=\lbrace\langle x,r,w\rangle: \ \mathcal{M}\models (x<u_{0} \wedge w<d \wedge r<d \wedge [f_{r}(\bar{u},x,(a)_{w})\downarrow]) \rbrace. \end{align*} $$
$$ \begin{align*} L':=\lbrace\langle x,r,w\rangle: \ \mathcal{M}\models (x<u_{0} \wedge w<d \wedge r<d \wedge [f_{r}(\bar{u},x,(a)_{w})\downarrow]) \rbrace. \end{align*} $$
The rest of the argument goes smoothly by modifying the “forth” stage according to the above changes, and this completes the proof.
Corollary 3.5. Assume
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard,
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard,
![]() $ I $
is a proper cut of
$ I $
is a proper cut of
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ \mathcal {M}_{0} $
is an
$ \mathcal {M}_{0} $
is an
![]() $ I$
-small
$ I$
-small
![]() $ \Sigma _{1} $
-elementary submodel of
$ \Sigma _{1} $
-elementary submodel of
![]() $\mathcal {M}$
. Then the following are equivalent:
$\mathcal {M}$
. Then the following are equivalent:
-
(1)
 $ I $
is strong in
$ I $
is strong in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(2) There exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ { M_{0}=\mathrm {Fix}(j)} $
.
$ { M_{0}=\mathrm {Fix}(j)} $
.
Proof Suppose
![]() ${ M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
, for some
${ M_{0}=\lbrace (a)_{i}: \ i\in I\rbrace } $
, for some
![]() $ a\in M $
such that
$ a\in M $
such that
![]() $ (a)_{i}\neq (a)_{j} $
for all distinct
$ (a)_{i}\neq (a)_{j} $
for all distinct
![]() $ i, j\in I $
.
$ i, j\in I $
.
![]() $ (1)\Rightarrow (2) $
: If
$ (1)\Rightarrow (2) $
: If
![]() $ M_{0}=I $
, then by Theorem 2.4(2), we are done. So suppose
$ M_{0}=I $
, then by Theorem 2.4(2), we are done. So suppose
![]() $ I\subsetneq M_{0} $
. First, by using Theorem 3.4 let
$ I\subsetneq M_{0} $
. First, by using Theorem 3.4 let
![]() $ h $
be some proper initial self-embedding of
$ h $
be some proper initial self-embedding of
![]() $ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
$ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
![]() $ \mathrm {Fix}(h)=M_{0} $
. Moreover, fix some
$ \mathrm {Fix}(h)=M_{0} $
. Moreover, fix some
![]() $b\in \mathrm {H}^{1}(\mathcal {M};M_{0})\setminus M_{0} $
such that
$b\in \mathrm {H}^{1}(\mathcal {M};M_{0})\setminus M_{0} $
such that
![]() $ h( \mathrm {H}^{1}(\mathcal {M};M_{0}))<b $
. Now, by using strong
$ h( \mathrm {H}^{1}(\mathcal {M};M_{0}))<b $
. Now, by using strong
![]() $ \Sigma _{1}$
-Collection in
$ \Sigma _{1}$
-Collection in
![]() $ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
, and since
$ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
, and since
![]() $ \mathrm {H}^{1}(\mathcal {M};M_{0})\prec _{\Sigma _{1}}\mathcal {M} $
, we can find some
$ \mathrm {H}^{1}(\mathcal {M};M_{0})\prec _{\Sigma _{1}}\mathcal {M} $
, we can find some
![]() $ d\in \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
$ d\in \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
Therefore, by Theorems 2.1 and 2.3 and Remark 1, there exists some proper initial embedding
![]() $ k:\mathcal {M}\hookrightarrow \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
$ k:\mathcal {M}\hookrightarrow \mathrm {H}^{1}(\mathcal {M};M_{0}) $
such that
![]() $ M_{0}\subseteq \mathrm {Fix}(k) $
,
$ M_{0}\subseteq \mathrm {Fix}(k) $
,
![]() $ k(M)<d, $
and
$ k(M)<d, $
and
![]() $ b\in k(M) $
(note that since
$ b\in k(M) $
(note that since
![]() $ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
is an initial segment of
$ \mathrm {H}^{1}(\mathcal {M};M_{0}) $
is an initial segment of
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $ \mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathrm {H}^{1}(\mathcal {M};M_{0})) $
). Finally, we put
$ \mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathrm {H}^{1}(\mathcal {M};M_{0})) $
). Finally, we put
![]() $ j:=k^{-1}hk $
. It is easy to check that
$ j:=k^{-1}hk $
. It is easy to check that
![]() $ j $
is a well-defined proper initial self-embedding of
$ j $
is a well-defined proper initial self-embedding of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \mathrm {Fix}(j)=M_{0} $
.
$ \mathrm {Fix}(j)=M_{0} $
.
![]() $ (2)\Rightarrow (1) $
: We combine the methods used in the proofs of Theorems 5.1 and 6.1 of [Reference Bahrami and Enayat1]. Suppose I is not strong; i.e., there exists some coded function
$ (2)\Rightarrow (1) $
: We combine the methods used in the proofs of Theorems 5.1 and 6.1 of [Reference Bahrami and Enayat1]. Suppose I is not strong; i.e., there exists some coded function
![]() $ f $
in
$ f $
in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ I\subseteq \mathrm {Dom}(f) $
, and the set
$ I\subseteq \mathrm {Dom}(f) $
, and the set
![]() $ {D:=\lbrace f(i): \ i\in I \wedge I<f(i)\rbrace } $
is downward cofinal in
$ {D:=\lbrace f(i): \ i\in I \wedge I<f(i)\rbrace } $
is downward cofinal in
![]() $ M\setminus I $
.
$ M\setminus I $
.
Let
![]() $ b\in M\setminus M_{0} $
and
$ b\in M\setminus M_{0} $
and
![]() $ g:=j(f) $
. For every
$ g:=j(f) $
. For every
![]() $ k\in M $
, we put
$ k\in M $
, we put
Since
![]() $ A_{k} $
is bounded and
$ A_{k} $
is bounded and
![]() $ \Delta _{1}$
-definable, it is coded by some
$ \Delta _{1}$
-definable, it is coded by some
![]() $ s_{k} $
in
$ s_{k} $
in
![]() $\mathcal {M}$
. Moreover, the function
$\mathcal {M}$
. Moreover, the function
![]() $ k\mapsto s_{k} $
is
$ k\mapsto s_{k} $
is
![]() $ \Delta _{1}$
-definable in
$ \Delta _{1}$
-definable in
![]() $ \mathcal {M} $
. Now, we define
$ \mathcal {M} $
. Now, we define
So note that:
-
(I) For every
 $ k> I $
, we have
$ k> I $
, we have
 $ \mathrm {Th}_{\Delta _{0}}(\mathcal {M};b,\{(a)_{i}\}_{i\in I})\subseteq \mathrm {Th}_{\Delta _{0}}(\mathcal {M};h(k),\{(a)_{i}\}_{i\in I})$
.
$ \mathrm {Th}_{\Delta _{0}}(\mathcal {M};b,\{(a)_{i}\}_{i\in I})\subseteq \mathrm {Th}_{\Delta _{0}}(\mathcal {M};h(k),\{(a)_{i}\}_{i\in I})$
. -
(II) For every
 $ i\in I $
,
$ i\in I $
,
 $ h(i)$
is well-defined and inside
$ h(i)$
is well-defined and inside
 $ M_{0}=\mathrm {Fix}(j) $
; the reason behind this statement is that for every
$ M_{0}=\mathrm {Fix}(j) $
; the reason behind this statement is that for every
 $ i\in I $
we consider the following set: Then, by Lemma 3.3,
$ i\in I $
we consider the following set: Then, by Lemma 3.3, $$ \begin{align*} B_{i}:=\lbrace\langle r,\epsilon\rangle: \ \mathcal{M}\models \exists y<i ((a)_{y}=\epsilon\wedge \langle r,y\rangle\mathrm{E}s_{i})\rbrace. \end{align*} $$
$$ \begin{align*} B_{i}:=\lbrace\langle r,\epsilon\rangle: \ \mathcal{M}\models \exists y<i ((a)_{y}=\epsilon\wedge \langle r,y\rangle\mathrm{E}s_{i})\rbrace. \end{align*} $$
 $ B_{i} $
is coded by some
$ B_{i} $
is coded by some
 $ \alpha _{i}\in M_{0}=\mathrm {Fix}(j) $
. So it holds that As a result, since
$ \alpha _{i}\in M_{0}=\mathrm {Fix}(j) $
. So it holds that As a result, since $$ \begin{align*} \mathcal{M}\models h(i)=\mu_{x}(\forall \langle r,\epsilon\rangle\mathrm{E}\alpha_{i} \ (\mathrm{Sat}_{\Delta_{0}}(\delta_{r}(\epsilon,x))). \end{align*} $$
$$ \begin{align*} \mathcal{M}\models h(i)=\mu_{x}(\forall \langle r,\epsilon\rangle\mathrm{E}\alpha_{i} \ (\mathrm{Sat}_{\Delta_{0}}(\delta_{r}(\epsilon,x))). \end{align*} $$
 $ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, statement (II) holds.
$ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, statement (II) holds.
Now, let
![]() $ h':=j(h) $
. So for all
$ h':=j(h) $
. So for all
![]() $ i\in I $
, and all
$ i\in I $
, and all
![]() $ u<i $
such that
$ u<i $
such that
![]() $ f(u)<i $
, statement (II) implies that
$ f(u)<i $
, statement (II) implies that
Therefore, for all
![]() $ i\in I $
,
$ i\in I $
,
![]() $ \mathcal {M}\models \varphi (i,f,g,h,h') $
, where
$ \mathcal {M}\models \varphi (i,f,g,h,h') $
, where
![]() $ \varphi (i,f,g,h,h') $
is the following
$ \varphi (i,f,g,h,h') $
is the following
![]() $ \Delta _{1}$
-formula:
$ \Delta _{1}$
-formula:
So by
![]() $ \Sigma _{1} $
-Overspill in
$ \Sigma _{1} $
-Overspill in
![]() $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
![]() $ s> I $
such that
$ s> I $
such that
Since
![]() $ D $
is downward cofinal in
$ D $
is downward cofinal in
![]() $ M\setminus I $
, there is some
$ M\setminus I $
, there is some
![]() $ i_{0}\in I $
such that
$ i_{0}\in I $
such that
![]() $ I<f(i_{0})<s $
. Let
$ I<f(i_{0})<s $
. Let
![]() $ c:=h(f(i_{0})) $
. On one hand, by (I),
$ c:=h(f(i_{0})) $
. On one hand, by (I),
![]() $ \mathrm {Th}_{\Delta _{0}}(\mathcal {M};b,\{(a)_{i}\}_{i\in I})\subseteq \mathrm {Th}_{\Delta _{0}}(\mathcal {M};c,\{(a)_{i}\}_{i\in I})$
. As a result, because
$ \mathrm {Th}_{\Delta _{0}}(\mathcal {M};b,\{(a)_{i}\}_{i\in I})\subseteq \mathrm {Th}_{\Delta _{0}}(\mathcal {M};c,\{(a)_{i}\}_{i\in I})$
. As a result, because
![]() $ b\notin M_{0} $
, we have
$ b\notin M_{0} $
, we have
![]() $ c\notin M_{0}=\mathrm {Fix}(j) $
. On the other hand
$ c\notin M_{0}=\mathrm {Fix}(j) $
. On the other hand
![]() $ (\spadesuit ) $
implies that
$ (\spadesuit ) $
implies that
As a result, I has to be strong in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
4 Strongness of the standard cut and fixed points
In this section, we will show some properties of
![]() $ \mathrm {Fix}(j) $
, when
$ \mathrm {Fix}(j) $
, when
![]() $ \mathbb {N} $
is not strong in
$ \mathbb {N} $
is not strong in
![]() $\mathcal {M}$
. Then we will derive some criteria for strongness of
$\mathcal {M}$
. Then we will derive some criteria for strongness of
![]() $ \mathbb {N} $
in a countable nonstandard model of
$ \mathbb {N} $
in a countable nonstandard model of
![]() $ \mathrm {I}\Sigma _{1} $
in terms of sets of fixed points of its initial self-embeddings.
$ \mathrm {I}\Sigma _{1} $
in terms of sets of fixed points of its initial self-embeddings.
Lemma 4.1. Suppose
![]() $ \mathcal {M}$
is a nonstandard model of
$ \mathcal {M}$
is a nonstandard model of
![]() $ \mathrm {I}\Sigma _{1} $
in which
$ \mathrm {I}\Sigma _{1} $
in which
![]() $ \mathbb {N} $
is not strong. Then for any self-embedding
$ \mathbb {N} $
is not strong. Then for any self-embedding
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
the following hold:
$\mathcal {M}$
the following hold:
-
(1)
 $ \mathrm {Fix}(j) $
is 1-tall.
$ \mathrm {Fix}(j) $
is 1-tall. -
(2) If
 $ \mathrm {Fix}(j)$
is a countable model of
$ \mathrm {Fix}(j)$
is a countable model of
 $\mathrm {B}\Sigma _{1} $
, then it is 1-extendable.
$\mathrm {B}\Sigma _{1} $
, then it is 1-extendable.
Proof
-
(1) Let
 $ a\in \mathrm {Fix}(j) $
be arbitrary and fixed. Since
$ a\in \mathrm {Fix}(j) $
be arbitrary and fixed. Since
 $ \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M} $
, it suffices to prove that
$ \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M} $
, it suffices to prove that
 $ \mathrm {K}^{1}(\mathcal {M};a) $
is not cofinal in
$ \mathrm {K}^{1}(\mathcal {M};a) $
is not cofinal in
 $ \mathrm {Fix}(j) $
. Since
$ \mathrm {Fix}(j) $
. Since
 $ \mathcal {M}\models \mathrm {B}^{+}\Sigma _{1} $
, there exists some
$ \mathcal {M}\models \mathrm {B}^{+}\Sigma _{1} $
, there exists some
 $ t_{0}\in M $
such that
$ t_{0}\in M $
such that
 $\mathrm {K}^{1}(\mathcal {M};a)<t_{0} $
. Moreover, by Lemma 2.5(2) there exists some
$\mathrm {K}^{1}(\mathcal {M};a)<t_{0} $
. Moreover, by Lemma 2.5(2) there exists some
 $ t_{00}\in \mathrm {Fix}(j) $
such that
$ t_{00}\in \mathrm {Fix}(j) $
such that
 ${\mathrm {Th}_{\Sigma _{1}}(\mathcal {M};t_{0},a)\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};t_{00},a)}$
. Therefore,
${\mathrm {Th}_{\Sigma _{1}}(\mathcal {M};t_{0},a)\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};t_{00},a)}$
. Therefore,
 $ \mathrm {K}^{1}(\mathcal {M};a)<t_{00} $
.
$ \mathrm {K}^{1}(\mathcal {M};a)<t_{00} $
. -
(2) By Theorem 2.2(2), and part (1) of this lemma, it suffices to prove that
 $ \mathbb {N} $
is not
$ \mathbb {N} $
is not
 $ \Pi _{1}$
-definable in
$ \Pi _{1}$
-definable in
 $ \mathrm {Fix}(j) $
. Suppose not; i.e.,
$ \mathrm {Fix}(j) $
. Suppose not; i.e.,
 $ \mathbb {N} $
is definable in
$ \mathbb {N} $
is definable in
 $ \mathrm {Fix}(j) $
by some
$ \mathrm {Fix}(j) $
by some
 $ \Pi _{1}$
-formula
$ \Pi _{1}$
-formula
 $ \pi (x) $
. By Lemma 2.5(1),
$ \pi (x) $
. By Lemma 2.5(1),
 $ \mathrm {Fix}(j)\cap M\setminus \mathbb {N} $
is downward cofinal in
$ \mathrm {Fix}(j)\cap M\setminus \mathbb {N} $
is downward cofinal in
 $ M\setminus \mathbb {N} $
. So by
$ M\setminus \mathbb {N} $
. So by
 $ \Sigma _{1}$
-Underspill in
$ \Sigma _{1}$
-Underspill in
 $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
 $ n\in \mathbb {N} $
such that
$ n\in \mathbb {N} $
such that
 $ \mathcal {M}\models \neg \pi (n) $
, and consequently since
$ \mathcal {M}\models \neg \pi (n) $
, and consequently since
 $ \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M} $
,
$ \mathrm {Fix}(j)\prec _{\Sigma _{1}}\mathcal {M} $
,
 $ \mathrm {Fix}(j)\models \neg \pi (n) $
, which is a contradiction.
$ \mathrm {Fix}(j)\models \neg \pi (n) $
, which is a contradiction.
The following corollary generalizes Theorem 1.2:
Corollary 4.2. Let
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be countable and nonstandard in which
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be countable and nonstandard in which
![]() $ \mathbb {N} $
is not strong, and
$ \mathbb {N} $
is not strong, and
![]() $ j $
is an initial self-embedding of
$ j $
is an initial self-embedding of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
. Then
$ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
. Then
![]() $ \mathrm {Fix}(j) $
is isomorphic to a proper cut of
$ \mathrm {Fix}(j) $
is isomorphic to a proper cut of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof By Theorem 2.2(1) and the previous lemma, it is enough to prove that
![]() $ {\mathrm {SSy}(\mathrm {Fix}(j))=\mathrm {SSy}(\mathcal {M})} $
. So let
$ {\mathrm {SSy}(\mathrm {Fix}(j))=\mathrm {SSy}(\mathcal {M})} $
. So let
![]() $ X=\mathbb {N}\cap a_{\mathrm {E}} $
for some
$ X=\mathbb {N}\cap a_{\mathrm {E}} $
for some
![]() $ a\in M $
. Since
$ a\in M $
. Since
![]() $ \mathbb {N} $
is not strong in
$ \mathbb {N} $
is not strong in
![]() $\mathcal {M}$
, by Lemma 2.5(2) there exists some
$\mathcal {M}$
, by Lemma 2.5(2) there exists some
![]() $ b\in \mathrm {Fix}(j) $
such that
$ b\in \mathrm {Fix}(j) $
such that
![]() $ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};a)\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};b) $
. Therefore,
$ \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};a)\subseteq \mathrm {Th}_{\Sigma _{1}}(\mathcal {M};b) $
. Therefore,
![]() $ X=\mathbb {N}\cap b_{\mathrm {E}} $
, and this finishes the proof.
$ X=\mathbb {N}\cap b_{\mathrm {E}} $
, and this finishes the proof.
We conclude this section with a generalization of a similar result about automorphisms of countable recursively saturated models of
![]() $\mathrm {PA}$
in [Reference Kossak and Schmerl12]. Moreover, the following corollary defines Theorem 2.4(3).
$\mathrm {PA}$
in [Reference Kossak and Schmerl12]. Moreover, the following corollary defines Theorem 2.4(3).
Corollary 4.3. Let
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be countable and nonstandard. Then the following are equivalent:
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
be countable and nonstandard. Then the following are equivalent:
-
(1)
 $ \mathbb {N} $
is strong in
$ \mathbb {N} $
is strong in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(2) There exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)=\mathrm {K}^{1}(\mathcal {M}). $
$ \mathrm {Fix}(j)=\mathrm {K}^{1}(\mathcal {M}). $
-
(3) There exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
, and some small
$\mathcal {M}$
, and some small
 $ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, such that
$ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
, such that
 $ \mathrm {Fix}(j)= M_{0}. $
$ \mathrm {Fix}(j)= M_{0}. $
-
(4) For every small
 $ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
there exists some proper initial self-embedding
$ \mathcal {M}_{0}\prec _{\Sigma _{1}}\mathcal {M} $
there exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)= M_{0}. $
$ \mathrm {Fix}(j)= M_{0}. $
-
(5) There exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)\subseteq \mathrm {I}^{1}(\mathcal {M}) $
.
$ \mathrm {Fix}(j)\subseteq \mathrm {I}^{1}(\mathcal {M}) $
.
If
![]() $ \mathcal {M}\models \mathrm {PA} $
and it is recursively saturated, then the above statements are equivalent to the following:
$ \mathcal {M}\models \mathrm {PA} $
and it is recursively saturated, then the above statements are equivalent to the following:
-
(6) There exists some proper initial self-embedding
 $ j $
of
$ j $
of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
and it is isomorphic to no proper initial segments of
$ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
and it is isomorphic to no proper initial segments of
 $\mathcal {M}$
.
$\mathcal {M}$
.
Proof The equivalences of statements (1)–(5) is a straightforward implication of Corollary 3.5 and Lemma 4.1(1). Moreover,
![]() $ (6)\Rightarrow (1) $
holds by Corollary 4.2. In order to prove
$ (6)\Rightarrow (1) $
holds by Corollary 4.2. In order to prove
![]() $ (4)\Rightarrow (6) $
, similar to the proof of Theorem 3.2(3), we will find some small recursively saturated elementary submodel
$ (4)\Rightarrow (6) $
, similar to the proof of Theorem 3.2(3), we will find some small recursively saturated elementary submodel
![]() $ \mathcal {M}_{0} $
of
$ \mathcal {M}_{0} $
of
![]() $\mathcal {M}$
. So statement (4) will provide us with a proper initial self-embedding
$\mathcal {M}$
. So statement (4) will provide us with a proper initial self-embedding
![]() $ j $
of
$ j $
of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \mathrm {Fix}(j)=M_{0} $
. Clearly
$ \mathrm {Fix}(j)=M_{0} $
. Clearly
![]() $ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
. Moreover, as we mentioned in the beginning of Section 3,
$ \mathrm {Fix}(j)\models \mathrm {B}\Sigma _{1} $
. Moreover, as we mentioned in the beginning of Section 3,
![]() $ \mathrm {SSy}(\mathcal {M}_{0})\neq \mathrm {SSy}(\mathcal {M}) $
. As a result,
$ \mathrm {SSy}(\mathcal {M}_{0})\neq \mathrm {SSy}(\mathcal {M}) $
. As a result,
![]() $ \mathrm {Fix}(j) $
is isomorphic to no proper initial segment of
$ \mathrm {Fix}(j) $
is isomorphic to no proper initial segment of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
5 Extendability
In this section, we will study the extendability of initial embeddings. Most of the theorems of this section are generalizations of results about automorphisms of countable recursively saturated models of
![]() $\mathrm {PA}$
obtained in [Reference Kossak and Kotlarski10, Reference Kossak and Kotlarski11].
$\mathrm {PA}$
obtained in [Reference Kossak and Kotlarski10, Reference Kossak and Kotlarski11].
Definition 2. Suppose
![]() $ \mathcal {M}$
and
$ \mathcal {M}$
and
![]() $ \mathcal {N} $
are models of
$ \mathcal {N} $
are models of
![]() $\mathrm {I}\Sigma _{1} $
,
$\mathrm {I}\Sigma _{1} $
,
![]() $ \mathcal {M}_{0}$
and
$ \mathcal {M}_{0}$
and
![]() $\mathcal {N}_{0}$
are bounded submodels (or proper cuts) of
$\mathcal {N}_{0}$
are bounded submodels (or proper cuts) of
![]() $\mathcal {M} $
and
$\mathcal {M} $
and
![]() $ \mathcal {N,} $
respectively. We call an initial embedding
$ \mathcal {N,} $
respectively. We call an initial embedding
![]() $ j:\mathcal {M}_{0}\hookrightarrow \mathcal {N}_{0} $
an initial
$ j:\mathcal {M}_{0}\hookrightarrow \mathcal {N}_{0} $
an initial
![]() $ (\mathcal {M},\mathcal {N})$
-embedding if for every
$ (\mathcal {M},\mathcal {N})$
-embedding if for every
![]() $A\subseteq M_{0} $
it holds that
$A\subseteq M_{0} $
it holds that
 $$ \begin{align*} &\qquad A \in \mathrm{SSy}_{I}(\mathcal{M}) \text{ iff } j( A) \in\mathrm{SSy}_{J}(\mathcal{N}),\\ &\text{ where } I:=\mathrm{I}^{1}(\mathcal{M};M_{0}), \text{ and } J:=\mathrm{I}^{1}(\mathcal{N};j(M_{0})). \end{align*} $$
$$ \begin{align*} &\qquad A \in \mathrm{SSy}_{I}(\mathcal{M}) \text{ iff } j( A) \in\mathrm{SSy}_{J}(\mathcal{N}),\\ &\text{ where } I:=\mathrm{I}^{1}(\mathcal{M};M_{0}), \text{ and } J:=\mathrm{I}^{1}(\mathcal{N};j(M_{0})). \end{align*} $$
If
![]() $ \mathcal {M}=\mathcal {N} $
, we call such
$ \mathcal {M}=\mathcal {N} $
, we call such
![]() $ j $
an initial
$ j $
an initial
![]() $\mathcal {M}$
-embedding.
$\mathcal {M}$
-embedding.
First, in the next lemma we will show that the condition in the above definition, i.e., preserving coded subsets, is a necessary condition for extendability of an initial embedding.
Lemma 5.1. Suppose
![]() $ \mathcal {M}$
and
$ \mathcal {M}$
and
![]() $ \mathcal {N} $
are models of
$ \mathcal {N} $
are models of
![]() $\mathrm {I}\Sigma _{1} $
,
$\mathrm {I}\Sigma _{1} $
,
![]() $ \mathcal {M}_{0}\subseteq \mathcal {M}$
and
$ \mathcal {M}_{0}\subseteq \mathcal {M}$
and
![]() $\mathcal {N}_{0}\subseteq \mathcal {N}$
are bounded submodels (or proper cuts), and
$\mathcal {N}_{0}\subseteq \mathcal {N}$
are bounded submodels (or proper cuts), and
![]() $ j:\mathcal {M}_{0}\hookrightarrow \mathcal {N}_{0} $
is an initial embedding. If
$ j:\mathcal {M}_{0}\hookrightarrow \mathcal {N}_{0} $
is an initial embedding. If
![]() $ j $
is extendable to some initial embedding
$ j $
is extendable to some initial embedding
![]() $ \hat {j}:\mathcal {M}\hookrightarrow \mathcal {N} $
, then
$ \hat {j}:\mathcal {M}\hookrightarrow \mathcal {N} $
, then
![]() $ j $
is an initial
$ j $
is an initial
![]() $ (\mathcal {M},\mathcal {N})$
-embedding.
$ (\mathcal {M},\mathcal {N})$
-embedding.
Proof Put
![]() $ I:=\mathrm {I}^{1}(\mathcal {M};M_{0}) $
,
$ I:=\mathrm {I}^{1}(\mathcal {M};M_{0}) $
,
![]() $ J:=\mathrm {I}^{1}(\mathcal {N};j(M_{0})) $
, and let
$ J:=\mathrm {I}^{1}(\mathcal {N};j(M_{0})) $
, and let
![]() $ A\subseteq M_{0} $
be arbitrary. If
$ A\subseteq M_{0} $
be arbitrary. If
![]() $ {A=I\cap (\alpha _{\mathrm {E}})^{\mathcal {M}}} $
for some
$ {A=I\cap (\alpha _{\mathrm {E}})^{\mathcal {M}}} $
for some
![]() $ \alpha $
in
$ \alpha $
in
![]() $\mathcal {M}$
, then clearly
$\mathcal {M}$
, then clearly
![]() $ j(A)=J\cap ((\hat {j}(\alpha ))_{\mathrm {E}})^{\mathcal {N}}$
. Conversely, suppose
$ j(A)=J\cap ((\hat {j}(\alpha ))_{\mathrm {E}})^{\mathcal {N}}$
. Conversely, suppose
![]() $ j( A)\in \mathrm {SSy}_{J}(\mathcal {N}) $
. Since
$ j( A)\in \mathrm {SSy}_{J}(\mathcal {N}) $
. Since
![]() $ M_{0} $
is bounded in
$ M_{0} $
is bounded in
![]() $\mathcal {M}$
, we have
$\mathcal {M}$
, we have
![]() $ J\subsetneq _{e}\hat {j}( M) $
. As a result,
$ J\subsetneq _{e}\hat {j}( M) $
. As a result,
![]() $ j(A)\in \mathrm {SSy}_{J}(\hat {j}( M)) $
, which implies that
$ j(A)\in \mathrm {SSy}_{J}(\hat {j}( M)) $
, which implies that
![]() $A\in \mathrm {SSy}_{I}(\mathcal {M}) $
.
$A\in \mathrm {SSy}_{I}(\mathcal {M}) $
.
Converse of the above lemma holds, when
![]() $ \mathcal {M}_{0} $
and
$ \mathcal {M}_{0} $
and
![]() $ j(M_{0}) $
are
$ j(M_{0}) $
are
![]() $ \Sigma _{1} $
-elementary initial segments of
$ \Sigma _{1} $
-elementary initial segments of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $ \mathcal {N} $
.
$ \mathcal {N} $
.
Theorem 5.2. Suppose
![]() $ \mathcal {M}$
and
$ \mathcal {M}$
and
![]() $ \mathcal {N} $
are countable and nonstandard models of
$ \mathcal {N} $
are countable and nonstandard models of
![]() $\mathrm {I}\Sigma _{1} $
, and
$\mathrm {I}\Sigma _{1} $
, and
![]() $ I$
and
$ I$
and
![]() $ J $
are
$ J $
are
![]() $ \Sigma _{1} $
-elementary initial segments of
$ \Sigma _{1} $
-elementary initial segments of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $ \mathcal {N} $
, respectively. Then for any isomorphism
$ \mathcal {N} $
, respectively. Then for any isomorphism
![]() $ {j: I\rightarrow J} $
which is an initial
$ {j: I\rightarrow J} $
which is an initial
![]() $ (\mathcal {M},\mathcal {N})$
-embedding and each
$ (\mathcal {M},\mathcal {N})$
-embedding and each
![]() $ b>J $
, there exists some proper initial embedding
$ b>J $
, there exists some proper initial embedding
![]() $ \hat {j}:\mathcal {M}\hookrightarrow \mathcal {N} $
such that
$ \hat {j}:\mathcal {M}\hookrightarrow \mathcal {N} $
such that
![]() $ \hat {j}\upharpoonright _{I}=j $
and
$ \hat {j}\upharpoonright _{I}=j $
and
![]() $ \hat {j}(M)<b $
.
$ \hat {j}(M)<b $
.
Sketch of proof.
The proof is conducted by a back-and-forth argument similar to the one used in the proof of [Reference Bahrami and Enayat1, Theorem 3.3]; we will build finite partial functions
![]() $ \bar {u}\mapsto \bar {v} $
such that the following induction hypothesis holds:
$ \bar {u}\mapsto \bar {v} $
such that the following induction hypothesis holds:
 $$ \begin{align*} &\text{If } \mathcal{M}\models [f(\bar{u},i)\downarrow], \text{ then } \mathcal{N}\models [f(\bar{v},j(i))\downarrow] ^{<b},\\ & \quad \text{for every } f\in\mathcal{F} \text{ and } i\in I. \end{align*} $$
$$ \begin{align*} &\text{If } \mathcal{M}\models [f(\bar{u},i)\downarrow], \text{ then } \mathcal{N}\models [f(\bar{v},j(i))\downarrow] ^{<b},\\ & \quad \text{for every } f\in\mathcal{F} \text{ and } i\in I. \end{align*} $$
For the “forth” steps, if
![]() $ \bar {u}\mapsto \bar {v} $
is built, for given
$ \bar {u}\mapsto \bar {v} $
is built, for given
![]() $ m\in M $
we define
$ m\in M $
we define
Then, let
![]() $ h\in M $
such that
$ h\in M $
such that
![]() $ H=I\cap h_{\mathrm {E}} $
. Since
$ H=I\cap h_{\mathrm {E}} $
. Since
![]() $ j $
is an initial
$ j $
is an initial
![]() $ (\mathcal {M},\mathcal {N}) $
-embedding, there exists some
$ (\mathcal {M},\mathcal {N}) $
-embedding, there exists some
![]() $ h'\in N $
such that
$ h'\in N $
such that
![]() $ j(H)=J\cap h^{\prime }_{\mathrm {E}} $
. Therefore, by induction hypothesis for every
$ j(H)=J\cap h^{\prime }_{\mathrm {E}} $
. Therefore, by induction hypothesis for every
![]() $ s\in I $
it holds that
$ s\in I $
it holds that
-
(1):
 $ \mathcal {N}\models \exists x, w<b \ \forall \langle r,i\rangle <j(s) \ (\langle r,i\rangle \mathrm {E}h'\rightarrow [f_{r}(\bar {v},x,i))\downarrow ]^{<w} ) $
.
$ \mathcal {N}\models \exists x, w<b \ \forall \langle r,i\rangle <j(s) \ (\langle r,i\rangle \mathrm {E}h'\rightarrow [f_{r}(\bar {v},x,i))\downarrow ]^{<w} ) $
.Since
 $ j $
is onto, statement (1) implies that for every
$ j $
is onto, statement (1) implies that for every
 $ t\in J $
it hold that
$ t\in J $
it hold that -
(2):
 $ \mathcal {N}\models \exists x, w<b \ \forall \langle r,i\rangle <t \ (\langle r,i\rangle \mathrm {E}h^{'}\rightarrow [f_{r}(\bar {v},x,i))\downarrow ]^{<w}) $
.
$ \mathcal {N}\models \exists x, w<b \ \forall \langle r,i\rangle <t \ (\langle r,i\rangle \mathrm {E}h^{'}\rightarrow [f_{r}(\bar {v},x,i))\downarrow ]^{<w}) $
.
Therefore, by using
![]() $ \Sigma _{1}$
-Overspill in
$ \Sigma _{1}$
-Overspill in
![]() $ \mathcal {N} $
, we will find some image for
$ \mathcal {N} $
, we will find some image for
![]() $ m $
, for which induction hypothesis holds. The “back” stages can be done similarly.⊣
$ m $
, for which induction hypothesis holds. The “back” stages can be done similarly.⊣
The proof of the above theorem can also be modified for
![]() $ I$
-small submodels.
$ I$
-small submodels.
Theorem 5.3. Suppose
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard, I is a strong cut of
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard, I is a strong cut of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $ \mathcal {M}_{0} $
is an
$ \mathcal {M}_{0} $
is an
![]() $ I$
-small
$ I$
-small
![]() $ \Sigma _{1} $
-elementary submodel of
$ \Sigma _{1} $
-elementary submodel of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ M_{0}:=\{(a)_{i}: i\in I\} $
, and
$ M_{0}:=\{(a)_{i}: i\in I\} $
, and
![]() $ j $
is an initial embedding of
$ j $
is an initial embedding of
![]() $ \mathcal {M}_{0} $
such that
$ \mathcal {M}_{0} $
such that
![]() $ j(I)\subseteq _{e}\mathcal {M} $
. Then the following are equivalent:
$ j(I)\subseteq _{e}\mathcal {M} $
. Then the following are equivalent:
-
(1)
 $ j \upharpoonright _{I}$
is an initial
$ j \upharpoonright _{I}$
is an initial
 $ \mathcal {M}$
-embedding, and there exists some
$ \mathcal {M}$
-embedding, and there exists some
 $ b\in M $
such that
$ b\in M $
such that
 $ {\mathcal {M}\models j((a)_{i})=(b)_{j(i)}} $
for all
$ {\mathcal {M}\models j((a)_{i})=(b)_{j(i)}} $
for all
 $ i\in I $
.
$ i\in I $
. -
(2)
 $ j $
extends to some proper initial self-embedding of
$ j $
extends to some proper initial self-embedding of
 $\mathcal {M}$
.
$\mathcal {M}$
.
Sketch of proof.
![]() $(2) \Rightarrow (1) $
holds by Lemma 5.1. In order to prove
$(2) \Rightarrow (1) $
holds by Lemma 5.1. In order to prove
![]() $ (1)\Rightarrow (2) $
, we will use a similar argument to the proof of [Reference Bahrami and Enayat1, Theorem 3.3] to obtain an extension
$ (1)\Rightarrow (2) $
, we will use a similar argument to the proof of [Reference Bahrami and Enayat1, Theorem 3.3] to obtain an extension
![]() $ \hat {j} $
of
$ \hat {j} $
of
![]() $ j $
. For this purpose, first we will fix some
$ j $
. For this purpose, first we will fix some
![]() $ d\in M $
which is an upper bound for
$ d\in M $
which is an upper bound for
![]() $ M_{0} $
. Then, we will build finite partial functions
$ M_{0} $
. Then, we will build finite partial functions
![]() $ \bar {u}\mapsto \bar {v} $
such that the following induction hypothesis holds:
$ \bar {u}\mapsto \bar {v} $
such that the following induction hypothesis holds:
 $$ \begin{align*} \mathcal{M}\models &[f(\bar{u},(a)_{i})\downarrow]\rightarrow[f(\bar{v},(b)_{j(i)})\downarrow]^{<d} ,\\ &\text{for every } f\in\mathcal{F} \text{ and } i\in I. \end{align*} $$
$$ \begin{align*} \mathcal{M}\models &[f(\bar{u},(a)_{i})\downarrow]\rightarrow[f(\bar{v},(b)_{j(i)})\downarrow]^{<d} ,\\ &\text{for every } f\in\mathcal{F} \text{ and } i\in I. \end{align*} $$
Here, we outline the proof for the “back” steps and the proof of “forth” steps is left to the reader. Suppose
![]() $ \bar {u}\mapsto \bar {v} $
is built, and
$ \bar {u}\mapsto \bar {v} $
is built, and
![]() $ m<\max \{\bar {v}\} $
is given. We define
$ m<\max \{\bar {v}\} $
is given. We define
Then, let
![]() $ l\in M $
such that
$ l\in M $
such that
![]() $ L=j(I)\cap l_{\mathrm {E}} $
. Since
$ L=j(I)\cap l_{\mathrm {E}} $
. Since
![]() $ j\upharpoonright _{I} $
is an initial
$ j\upharpoonright _{I} $
is an initial
![]() $\mathcal {M}$
-embedding, then there exists some
$\mathcal {M}$
-embedding, then there exists some
![]() $ l'\in M $
such that
$ l'\in M $
such that
![]() $ j^{-1}(L)=I\cap l^{\prime }_{\mathrm {E}} $
. Moreover, by using Lemma 3.3, for every
$ j^{-1}(L)=I\cap l^{\prime }_{\mathrm {E}} $
. Moreover, by using Lemma 3.3, for every
![]() $ s\in I $
there exists some
$ s\in I $
there exists some
![]() $ (a)_{i_{s}}\in M_{0} $
which codes of the following subset of
$ (a)_{i_{s}}\in M_{0} $
which codes of the following subset of
![]() $ M_{0} $
:
$ M_{0} $
:
By
![]() $ \Pi _{1} $
-Overspill, it suffices to prove that for every
$ \Pi _{1} $
-Overspill, it suffices to prove that for every
![]() $ s\in I $
it holds that
$ s\in I $
it holds that
Suppose not; i.e., there exists some
![]() $ s\in I $
which for statement
$ s\in I $
which for statement
![]() $ (\star ) $
does not hold. So we have,
$ (\star ) $
does not hold. So we have,
-
(i):
 $ \mathcal {M}\models \forall x<\max \{\bar {u}\} \ \exists \langle r,i\rangle <s \ (\langle r,i\rangle \mathrm {E} l' \ \wedge [f_{r}(\bar {u},x,(a)_{i})\downarrow ] ) $
.
$ \mathcal {M}\models \forall x<\max \{\bar {u}\} \ \exists \langle r,i\rangle <s \ (\langle r,i\rangle \mathrm {E} l' \ \wedge [f_{r}(\bar {u},x,(a)_{i})\downarrow ] ) $
.As a result, by using
 $ \Sigma _{1} $
-Collection in
$ \Sigma _{1} $
-Collection in
 $\mathcal {M}$
, from statement
$\mathcal {M}$
, from statement
 $ (i) $
, induction hypothesis, and the way we chose
$ (i) $
, induction hypothesis, and the way we chose
 $(a)_{i_{s}} $
, we may conclude that
$(a)_{i_{s}} $
, we may conclude that -
(ii):
 $ \mathcal {M}\models \forall x<\max \{\bar {v}\} \ \exists \langle r,\epsilon \rangle \mathrm {E} (b)_{j(i_{s})} \ ( [f_{r}(\bar {v},x,\epsilon )\downarrow ]^{<d} ) $
.
$ \mathcal {M}\models \forall x<\max \{\bar {v}\} \ \exists \langle r,\epsilon \rangle \mathrm {E} (b)_{j(i_{s})} \ ( [f_{r}(\bar {v},x,\epsilon )\downarrow ]^{<d} ) $
.So by statement
 $ (ii) $
, there exists some
$ (ii) $
, there exists some
 $ \langle r,i\rangle <s $
such that
$ \langle r,i\rangle <s $
such that -
(iii):
 $ \mathcal {M}\models (\langle r,i\rangle \mathrm {E} l' \ \wedge \ [f_{j(r)}(\bar {v},m,(b)_{j(i)})\downarrow ]^{<d} ) $
.
$ \mathcal {M}\models (\langle r,i\rangle \mathrm {E} l' \ \wedge \ [f_{j(r)}(\bar {v},m,(b)_{j(i)})\downarrow ]^{<d} ) $
.
But statement
![]() $(iii)$
is in direct contradiction with the way we chose
$(iii)$
is in direct contradiction with the way we chose
![]() $ l' $
.⊣
$ l' $
.⊣
In the last theorem, we investigate whether we can control the set of fixed points, while extending an isomorphism to an initial self-embeddings with larger domain:
Theorem 5.4. Suppose
![]() $ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard, I is a strong
$ \mathcal {M}\models \mathrm {I}\Sigma _{1} $
is countable and nonstandard, I is a strong
![]() $ \Sigma _{1} $
-elementary initial segment of
$ \Sigma _{1} $
-elementary initial segment of
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $ j: I\rightarrow I $
is an isomorphism and an initial
$ j: I\rightarrow I $
is an isomorphism and an initial
![]() $ \mathcal {M}$
-embedding. Then there exists some proper initial self-embedding
$ \mathcal {M}$
-embedding. Then there exists some proper initial self-embedding
![]() $ \hat {j} $
of
$ \hat {j} $
of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \hat {j}\upharpoonright _{ I}=j $
, and
$ \hat {j}\upharpoonright _{ I}=j $
, and
![]() $ {\mathrm {Fix}(\hat {j})=\mathrm {Fix}(j)} $
.
$ {\mathrm {Fix}(\hat {j})=\mathrm {Fix}(j)} $
.
Sketch of proof.
First, we will fix some arbitrary
![]() $ a>I $
. Since I is strong in
$ a>I $
. Since I is strong in
![]() $\mathcal {M}$
, there exists some
$\mathcal {M}$
, there exists some
![]() $ b>I $
such that:
$ b>I $
such that:
So by Theorem 5.2, there exists some proper initial self-embedding
![]() $ \bar {j} $
of
$ \bar {j} $
of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $ \bar {j}\upharpoonright _{I}=j $
and
$ \bar {j}\upharpoonright _{I}=j $
and
![]() $ \bar {j}(M)<b $
. If
$ \bar {j}(M)<b $
. If
![]() $ \mathrm {Fix}(\bar {j})=\mathrm {Fix}(j) $
, then we are done. Otherwise, by using a similar argument to the proof of Theorem 3.4 (as we will briefly outline the modifications which should be made to the proof below), we will construct some proper initial self-embedding
$ \mathrm {Fix}(\bar {j})=\mathrm {Fix}(j) $
, then we are done. Otherwise, by using a similar argument to the proof of Theorem 3.4 (as we will briefly outline the modifications which should be made to the proof below), we will construct some proper initial self-embedding
![]() $ h $
of
$ h $
of
![]() $ \mathcal {N}:=\mathrm {H}^{1}(\mathcal {M};a) $
such that
$ \mathcal {N}:=\mathrm {H}^{1}(\mathcal {M};a) $
such that
![]() $ h\upharpoonright _{I}=j $
,
$ h\upharpoonright _{I}=j $
,
![]() $ \mathrm {Fix}(h)=\mathrm {Fix}(j) $
, and
$ \mathrm {Fix}(h)=\mathrm {Fix}(j) $
, and
![]() $ h(N)<b $
. If
$ h(N)<b $
. If
![]() $ \mathcal {M}=\mathcal {N} $
, then we are done. Otherwise, by using Theorem 2.3 we shall find some proper initial embedding
$ \mathcal {M}=\mathcal {N} $
, then we are done. Otherwise, by using Theorem 2.3 we shall find some proper initial embedding
![]() $ k:\mathcal {M}\hookrightarrow \mathcal {N} $
such that
$ k:\mathcal {M}\hookrightarrow \mathcal {N} $
such that
![]() $ I\subseteq \mathrm {I}_{\mathrm {fix}}(k) $
and
$ I\subseteq \mathrm {I}_{\mathrm {fix}}(k) $
and
![]() $ b\in k(M) $
. Finally, we put
$ b\in k(M) $
. Finally, we put
![]() $ \hat {j}:=k^{-1}hk $
.
$ \hat {j}:=k^{-1}hk $
.
In order to construct the aforementioned
![]() $ h $
, we will inductively build finite functions
$ h $
, we will inductively build finite functions
![]() $ \bar {u}\mapsto \bar {v} $
such that
$ \bar {u}\mapsto \bar {v} $
such that
 $$ \begin{align*} &\mathrm{P}(\bar{u},\bar{v})\equiv [f(\bar{u},i)\downarrow]\rightarrow[f(\bar{v},j(i))\downarrow]^{<b}, \text{ for all } f\in\mathcal{F} \text{ and } i\in I; \text{ and} \\ &\mathrm{Q}(\bar{u},\bar{v})\equiv \left(\begin{array}{@{}c@{}} [f(\bar{u},i)\downarrow] \wedge [f(\bar{v},j(i))\downarrow]^{<b}\wedge \\ f(\bar{u},i)\notin I\end{array}\right) \Rightarrow f(\bar{u},i)\neq f(\bar{v},j(i)), \text{ for all } f\in\mathcal{F}\\ & \text{and all } i\in I. \end{align*} $$
$$ \begin{align*} &\mathrm{P}(\bar{u},\bar{v})\equiv [f(\bar{u},i)\downarrow]\rightarrow[f(\bar{v},j(i))\downarrow]^{<b}, \text{ for all } f\in\mathcal{F} \text{ and } i\in I; \text{ and} \\ &\mathrm{Q}(\bar{u},\bar{v})\equiv \left(\begin{array}{@{}c@{}} [f(\bar{u},i)\downarrow] \wedge [f(\bar{v},j(i))\downarrow]^{<b}\wedge \\ f(\bar{u},i)\notin I\end{array}\right) \Rightarrow f(\bar{u},i)\neq f(\bar{v},j(i)), \text{ for all } f\in\mathcal{F}\\ & \text{and all } i\in I. \end{align*} $$
-
• For the first step of induction, we will take
 $ a\mapsto \bar {j}(a) $
; clearly
$ a\mapsto \bar {j}(a) $
; clearly
 $ \mathrm {P}(a,\bar {j}(a)) $
holds in
$ \mathrm {P}(a,\bar {j}(a)) $
holds in
 $\mathcal {M}$
. Moreover, by statement
$\mathcal {M}$
. Moreover, by statement
 $ (\star ) $
and since
$ (\star ) $
and since
 $ \mathrm {Fix}(\bar {j})<b $
, the property
$ \mathrm {Fix}(\bar {j})<b $
, the property
 $ \mathrm {Q}(a,\bar {j}(a)) $
also holds in
$ \mathrm {Q}(a,\bar {j}(a)) $
also holds in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
• Then suppose
 $ \bar {u}\mapsto \bar {v} $
is built. We will just mention the changes that should be made in the “forth” steps of Theorem 3.4, and “back” steps should be modified similarly:
$ \bar {u}\mapsto \bar {v} $
is built. We will just mention the changes that should be made in the “forth” steps of Theorem 3.4, and “back” steps should be modified similarly:-
– Suppose
 $ m\in N\setminus \{\bar {u}\} $
is given. By the definition of
$ m\in N\setminus \{\bar {u}\} $
is given. By the definition of
 $ \mathcal {N} $
, without loss of generality, we may assume that
$ \mathcal {N} $
, without loss of generality, we may assume that
 $ m\leq t(\bar {u},a) $
for some
$ m\leq t(\bar {u},a) $
for some
 $ t\in \mathcal {F} $
. Put Let
$ t\in \mathcal {F} $
. Put Let $$ \begin{align*} C:= \{\langle r,i\rangle\in I: \mathcal{N}\models[f_{r}(\bar{u},m,i)\downarrow]\wedge f_{r}(\bar{u},m,i)\notin\mathrm{K}^{1}(\mathcal{N};I\cup\{\bar{u}\}) \}. \end{align*} $$
$$ \begin{align*} C:= \{\langle r,i\rangle\in I: \mathcal{N}\models[f_{r}(\bar{u},m,i)\downarrow]\wedge f_{r}(\bar{u},m,i)\notin\mathrm{K}^{1}(\mathcal{N};I\cup\{\bar{u}\}) \}. \end{align*} $$
 $ \alpha ,\alpha '\in N $
such that
$ \alpha ,\alpha '\in N $
such that
 $ C=I\cap \alpha _{\mathrm {E}} $
and
$ C=I\cap \alpha _{\mathrm {E}} $
and
 $ j( C)=I\cap \alpha ^{\prime }_{\mathrm {E}} $
(note that since
$ j( C)=I\cap \alpha ^{\prime }_{\mathrm {E}} $
(note that since
 $ \mathcal {N} $
is a
$ \mathcal {N} $
is a
 $ \Sigma _{1} $
-elementary initial segment of
$ \Sigma _{1} $
-elementary initial segment of
 $\mathcal {M}$
containing I,
$\mathcal {M}$
containing I,
 $ j $
is an initial
$ j $
is an initial
 $ \mathcal {N}$
-embedding):
$ \mathcal {N}$
-embedding):
-
– Let
 $L:= \{\langle r,i\rangle \in I: \mathcal {N}\models [f_{r}(\bar {u},m,i)\downarrow ]\} $
,
$L:= \{\langle r,i\rangle \in I: \mathcal {N}\models [f_{r}(\bar {u},m,i)\downarrow ]\} $
,
 $ L=I\cap \beta _{\mathrm {E}} $
, and
$ L=I\cap \beta _{\mathrm {E}} $
, and
 $ j(L)=I\cap \beta ^{\prime }_{\mathrm {E}} $
for
$ j(L)=I\cap \beta ^{\prime }_{\mathrm {E}} $
for
 $ \beta ,\beta '\in N $
.
$ \beta ,\beta '\in N $
. -
– For every
 $ s\in \bar {j}(N) $
such that
$ s\in \bar {j}(N) $
such that
 $ \bar {j}(s')=s $
for some
$ \bar {j}(s')=s $
for some
 $ s'\in N $
, let
$ s'\in N $
, let  $$ \begin{align*} &p_{s}(y):= \lbrace y< t(\bar{v},\bar{j}(a))\rbrace\cup p_{s1}(y)\cup p_{s2}(y), \text{ where} \\ &{p_{s1}(y):=\lbrace\forall i<s(\langle n,i\rangle\mathrm{E}\beta'\rightarrow [f_{n}(\bar{v},y,i)\downarrow]^{<b}): \ n\in\mathbb{N}\rbrace,} \text{ and }\\ &p_{s2}(y):=\left\lbrace \forall w<s'\ \forall i<s \left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle n,w\rangle\mathrm{E}\alpha \ \wedge \ \langle n,i\rangle\mathrm{E}\alpha'\ \wedge \\ {}[f_{n}(\bar{v},y,i)\downarrow]^{<b}\end{array}\right) \rightarrow\\ f_{n}(\bar{u},m,w)\neq f_{n}(\bar{v},y,i)\end{array}\right) : \ n\in\mathbb{N} \right\rbrace. \end{align*} $$
$$ \begin{align*} &p_{s}(y):= \lbrace y< t(\bar{v},\bar{j}(a))\rbrace\cup p_{s1}(y)\cup p_{s2}(y), \text{ where} \\ &{p_{s1}(y):=\lbrace\forall i<s(\langle n,i\rangle\mathrm{E}\beta'\rightarrow [f_{n}(\bar{v},y,i)\downarrow]^{<b}): \ n\in\mathbb{N}\rbrace,} \text{ and }\\ &p_{s2}(y):=\left\lbrace \forall w<s'\ \forall i<s \left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle n,w\rangle\mathrm{E}\alpha \ \wedge \ \langle n,i\rangle\mathrm{E}\alpha'\ \wedge \\ {}[f_{n}(\bar{v},y,i)\downarrow]^{<b}\end{array}\right) \rightarrow\\ f_{n}(\bar{u},m,w)\neq f_{n}(\bar{v},y,i)\end{array}\right) : \ n\in\mathbb{N} \right\rbrace. \end{align*} $$
-
– In order to find some
 $ s>I $
such that
$ s>I $
such that
 $ s\in \bar {j}(N) $
and
$ s\in \bar {j}(N) $
and
 $ p_{s}(y) $
is finitely satisfiable, we will adapt the rest of the proof of Theorem 3.4 accordingly; for instance, we will mention two of these adaptations:
$ p_{s}(y) $
is finitely satisfiable, we will adapt the rest of the proof of Theorem 3.4 accordingly; for instance, we will mention two of these adaptations: -
(1) Let
 $ d'\in N $
such that
$ d'\in N $
such that
 $ d'>I $
and
$ d'>I $
and
 $ d:=\bar {j}(d') $
. Moreover, for every
$ d:=\bar {j}(d') $
. Moreover, for every
 $i,s,s'\in N$
, let
$i,s,s'\in N$
, let
 $ \Theta (s,s',i,\bar {u},m,\bar {v},b,\bar {j}(a),\alpha ,\alpha ',\beta ') $
be the following
$ \Theta (s,s',i,\bar {u},m,\bar {v},b,\bar {j}(a),\alpha ,\alpha ',\beta ') $
be the following
 $ \Delta _{0}$
-formula: Then, for every
$ \Delta _{0}$
-formula: Then, for every $$ \begin{align*} & \forall r<i \ \exists y\leq t(\bar{v},\bar{j}(a))\\ & \quad \times \left(\begin{array}{@{}c@{}} \forall w<s (\langle r,w\rangle\mathrm{E}\beta'\rightarrow [f_{r}(\bar{v},y,w)\downarrow]^{<b}) \ \wedge\\ \forall w<s\forall w'<s' \forall r'<i\left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle r',w'\rangle\mathrm{E}\alpha'\wedge\\ \langle r',w\rangle\mathrm{E}\alpha\wedge\\ {}[f_{r'}(\bar{v},y,(a)_{w})\downarrow]^{<b}\end{array}\right)\rightarrow \\ f_{r'}(\bar{u},m,w')\neq f_{r'}(\bar{v},y,w)\end{array}\right)\end{array}\!\right). \end{align*} $$
$$ \begin{align*} & \forall r<i \ \exists y\leq t(\bar{v},\bar{j}(a))\\ & \quad \times \left(\begin{array}{@{}c@{}} \forall w<s (\langle r,w\rangle\mathrm{E}\beta'\rightarrow [f_{r}(\bar{v},y,w)\downarrow]^{<b}) \ \wedge\\ \forall w<s\forall w'<s' \forall r'<i\left(\begin{array}{@{}c@{}} \left(\begin{array}{@{}c@{}}\langle r',w'\rangle\mathrm{E}\alpha'\wedge\\ \langle r',w\rangle\mathrm{E}\alpha\wedge\\ {}[f_{r'}(\bar{v},y,(a)_{w})\downarrow]^{<b}\end{array}\right)\rightarrow \\ f_{r'}(\bar{u},m,w')\neq f_{r'}(\bar{v},y,w)\end{array}\right)\end{array}\!\right). \end{align*} $$
 $ i\in M $
, we define Since I is strong, there exists some
$ i\in M $
, we define Since I is strong, there exists some $$ \begin{align*} \mathrm{G}(i):=\mathrm{max}\lbrace w<d': \ \mathcal{M}\models\exists x\leq d \ \Theta(x,w,i,\bar{u},m,\bar{v},b,\bar{j}(a),\alpha,\alpha',\beta') \rbrace. \end{align*} $$
$$ \begin{align*} \mathrm{G}(i):=\mathrm{max}\lbrace w<d': \ \mathcal{M}\models\exists x\leq d \ \Theta(x,w,i,\bar{u},m,\bar{v},b,\bar{j}(a),\alpha,\alpha',\beta') \rbrace. \end{align*} $$
 $ e'>I $
such that
$ e'>I $
such that
 $ e'\leq d' $
, and for all
$ e'\leq d' $
, and for all
 $ i\in I $
,
$ i\in I $
,
 $ \mathrm {G}(i)> I $
iff
$ \mathrm {G}(i)> I $
iff
 $ \mathrm {G}(i)>e' $
. Then, for every
$ \mathrm {G}(i)>e' $
. Then, for every
 $ i\in M $
put Again, since
$ i\in M $
put Again, since $$ \begin{align*} \kern-12pt l(i):=\mathrm{max}\left\lbrace x<\bar{j}(e'): \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} [\mathrm{G}(i)\downarrow]^{<d'} \ \wedge \ \mathrm{G}(i)>e'\ \wedge \\ \Theta(x,\mathrm{G}(i),i,\bar{u},m,\bar{v},b,\bar{j}(a),\alpha,\alpha',\beta') \end{array}\right) \right\rbrace .\end{align*} $$
$$ \begin{align*} \kern-12pt l(i):=\mathrm{max}\left\lbrace x<\bar{j}(e'): \ \mathcal{M}\models \left(\begin{array}{@{}c@{}} [\mathrm{G}(i)\downarrow]^{<d'} \ \wedge \ \mathrm{G}(i)>e'\ \wedge \\ \Theta(x,\mathrm{G}(i),i,\bar{u},m,\bar{v},b,\bar{j}(a),\alpha,\alpha',\beta') \end{array}\right) \right\rbrace .\end{align*} $$
 $ I $
is strong, there exists some
$ I $
is strong, there exists some
 $ e> I $
such that
$ e> I $
such that
 $ e\leq d $
, and for all
$ e\leq d $
, and for all
 $ i\in I $
,
$ i\in I $
,
 $ l(i)> I $
iff
$ l(i)> I $
iff
 $ l(i)>e $
. Then
$ l(i)>e $
. Then
 $ p_{e}(y) $
is a finitely satisfiable type.
$ p_{e}(y) $
is a finitely satisfiable type.
-
(2) Instead of the function
 $ \langle o(\diamondsuit ,y),h(\diamondsuit ,y)\rangle $
we need to define the following function: where
$ \langle o(\diamondsuit ,y),h(\diamondsuit ,y)\rangle $
we need to define the following function: where $$ \begin{align*} & \langle o(\diamondsuit,y),h(\diamondsuit,y),h'(\diamondsuit,y)\rangle\\ & \quad := \min\left\lbrace\langle n_{t},i,w\rangle\mathrm{E}\alpha_{s_{{}_{0}}}: \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\wedge\\ {}[f_{n_{t}}(\diamondsuit,y,i)\downarrow]^{<b(\diamondsuit,y)} \ \wedge\\ {}[g_{t}(\diamondsuit,w)\downarrow]^{<b(\diamondsuit,y)} \wedge\\ g_{t}(\diamondsuit,w)= f_{n_{t}}(\diamondsuit,y,i)\end{array}\right)\! \right\rbrace , \end{align*} $$
$$ \begin{align*} & \langle o(\diamondsuit,y),h(\diamondsuit,y),h'(\diamondsuit,y)\rangle\\ & \quad := \min\left\lbrace\langle n_{t},i,w\rangle\mathrm{E}\alpha_{s_{{}_{0}}}: \left(\begin{array}{@{}c@{}} [b(\diamondsuit,y)\downarrow]\wedge\\ {}[f_{n_{t}}(\diamondsuit,y,i)\downarrow]^{<b(\diamondsuit,y)} \ \wedge\\ {}[g_{t}(\diamondsuit,w)\downarrow]^{<b(\diamondsuit,y)} \wedge\\ g_{t}(\diamondsuit,w)= f_{n_{t}}(\diamondsuit,y,i)\end{array}\right)\! \right\rbrace , \end{align*} $$
 $ \alpha _{s_{0}}\in I $
is the code of the following subset of I: The rest of the adaptations should be made similar to statements (1) and (2) in order to construct h.⊣
$ \alpha _{s_{0}}\in I $
is the code of the following subset of I: The rest of the adaptations should be made similar to statements (1) and (2) in order to construct h.⊣ $$ \begin{align*} \{\langle n,i,w\rangle: \ \mathcal{M}\models i<s_{0}\wedge w<j^{-1}(s_{0})\wedge\langle n,w\rangle\mathrm{E}\alpha\wedge\langle n,i\rangle\mathrm{E}\alpha'\}. \end{align*} $$
$$ \begin{align*} \{\langle n,i,w\rangle: \ \mathcal{M}\models i<s_{0}\wedge w<j^{-1}(s_{0})\wedge\langle n,w\rangle\mathrm{E}\alpha\wedge\langle n,i\rangle\mathrm{E}\alpha'\}. \end{align*} $$
-
Acknowledgements
I would like to thank Ali Enayat for his comments on the very first draft of the paper. I am also grateful to the anonymous referee for the careful reading of this paper and many insightful comments and suggestions.
Funding
This research was supported by a grant from Iran National Science Foundation (INSF) (No. 99019371).