Published online by Cambridge University Press: 12 March 2014
Some 40 years ago, Dana Scott proved that every countable Scott set is the standard system of a model of PA. Two decades later, Knight and Nadel extended his result to Scott sets of size ω1. Here, I show that assuming the Proper Forcing Axiom (PFA), every A-proper Scott set is the standard system of a model of PA. I define that a Scott set 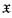 is proper if the quotient Boolean algebra
is proper if the quotient Boolean algebra 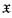 /Fin is a proper partial order and A-proper if
/Fin is a proper partial order and A-proper if 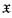 is additionally arithmetically closed. I also investigate the question of the existence of proper Scott sets.
is additionally arithmetically closed. I also investigate the question of the existence of proper Scott sets.