Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T05:22:10.058Z Has data issue: false hasContentIssue false
  • English
  • Français

Scales in K(ℝ) at the end of a weak gap

Published online by Cambridge University Press:  12 March 2014

J. R. Steel
J. R. Steel*
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, California 94720, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this note we shall prove

Theorem 0.1. Let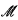be a countably ω-iterable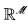-mouse which satisfies AD, and [α, β] a weak gap of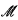. Suppose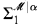is captured by mice with iteration strategies in 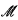∣α. Let n be least such that 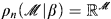; then we have that 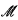believes that 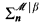has the Scale Property.

This complements the work of [5] on the construction of scales of minimal complexity on sets of reals in K(ℝ). Theorem 0.1 was proved there under the stronger hypothesis that all sets definable over 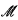are determined, although without the capturing hypothesis. (See [5, Theorem 4.14].) Unfortunately, this is more determinacy than would be available as an induction hypothesis in a core model induction. The capturing hypothesis, on the other hand, is available in such a situation. Since core model inductions are one of the principal applications of the construction of optimal scales, it is important to prove 0.1 as stated.

Our proof will incorporate a number of ideas due to Woodin which figure prominently in the weak gap case of the core model induction. It relies also on the connection between scales and iteration strategies with the Dodd-Jensen property first discovered in [3]. Let 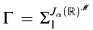be the pointclass at the beginning of the weak gap referred to in 0.1. In section 1, we use Woodin's ideas to construct a Γ-full a mouse 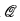having ω Woodin cardinals cofinal in its ordinals, together with an iteration strategy Σ which condenses well in the sense of [4, Def. 1.13]. In section 2, we construct the desired scale from 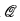and Σ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 2 , June 2008 , pp. 369 - 390
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ketchersid, R. O., Toward ADℝ from the Continuum Hypothesis and an ω1-dense ideal, Ph.D. thesis, University of California at Berkeley, 06 2000.Google Scholar
[2]Steel, J. R., Scales in L(ℝ), Cabal seminar 79–81 (Kechris, A. S., Martin, D. A., and Moscovakis, Y. N., editors), Lecture Notes in Mathematics, Springer-Verlag, 1983, pp. 107–156.CrossRefGoogle Scholar
[3]Steel, J. R., HODL(ℝ) is a core model below Θ, The Bulletin of Symbolic Logic, vol. 1 (1995), pp. 75–84.CrossRefGoogle Scholar
[4]Steel, J. R., PFA implies ADL(ℝ), this Journal, vol. 70 (2005), no. 4, pp. 1255–1296.Google Scholar
[5]Steel, J. R., Scales in K(ℝ), The Cabal Seminar I; Games, Scales, and Suslin Cardinals (Kechris, A. S., Loewe, B., and Steel, J., editors), Lecture Notes in Logic, vol. 31, ASL and Cambridge University Press, 2008, pp. 176–208.Google Scholar
[6]Steel, J. R., An outline of inner model theory, The handbook of set theory (Foreman, M., Kanamori, A., and Magidor, M., editors), to appear.Google Scholar
[7]Steel, J. R., A theorem of Woodin on mouse sets, available at http://www.math.berkeley.edu/~steel.Google Scholar
[8]Steel, J. R., Woodin's analysis of HODL(ℝ), available at http://www.math.berkeley.edu/~steel.Google Scholar