Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-30T19:39:39.595Z Has data issue: false hasContentIssue false
  • English
  • Français

QE commutative nilrings

Published online by Cambridge University Press:  12 March 2014

D. Saracino  and
C. Wood
D. Saracino
Affiliation:
Colgate University, Hamilton, New York 13346
C. Wood
Affiliation:
Wesleyan University, Middletown, Connecticut 06457
Get access Rights & Permissions [Opens in a new window]

Extract

If L is a first-order language, then an L-structure A is called quantifier-eliminable (QE) if every L-formula is equivalent in A to a formula without quantifiers.

The classification problem for QE groups and rings has received attention in work by Berline, Boffa, Cherlin, Feigner, Macintyre, Point, Rose, the present authors, and others. In [1], Berline and Cherlin reduced the problem for rings of prime characteristic p to that for nilrings, but also constructed 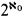countable QE nilrings of characteristic p. Likewise, in [3], we constructed 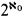countable QE nil-2 groups. Both results can be viewed as “nonstructure theorems”, in that they provide negative evidence for any attempt at classification. In the present paper we show that the situation is equally bad (or rich, depending on one's point of view) for commutative rings:

Theorem 1. For any odd prime p, there exist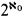countable QE commutative nilrings of characteristic p.

This solves a problem posed in [1]. We remark that the examples we produce are uniformly locally finite, hence ℵ0-categorical. A more algebraic description is that each of our rings R is uniformly locally finite (in fact, R3 = 0) and homogeneous, in the sense that any isomorphism of finitely generated subrings extends to an automorphism of R.

Theorem 1 does not cover the case p = 2, and we show that for commutative rings this case is in fact exceptional:

Theorem 2. There exist exactly two nonisomorphic countably infinite QE commutative nilrings of characteristic 2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 644 - 651
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Berline, C. and Cherlin, G., QE rings in characteristic p, Logic year 1979/80 (Proceedings of seminars and conference, Storrs, Connecticut), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 16–31.Google Scholar
[2]Berline, C. and Cherlin, G., QE nilrings of prime characteristic, Bulletin de la Société Mathématique de Belgique, Série A, vol. 33 (1981), pp. 3–17.Google Scholar
[3]Saracino, D. and Wood, C., QE nil-2 groups of exponent 4, Journal of Algebra, vol. 76 (1982), pp. 337–352.CrossRefGoogle Scholar
[4]Schmerl, J., Decidability and ℵ0-categoricity of theories of partially ordered sets, this Journal, vol. 45 (1980), pp. 585–611.Google Scholar