Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T18:10:41.695Z Has data issue: false hasContentIssue false
  • English
  • Français

A Perfect Set of Reals with Finite Self-Information

Published online by Cambridge University Press:  12 March 2014

Ian Herbert
Ian Herbert*
Affiliation:
Department of Mathematics, University of California, Berkeley 970 Evans Hall, Berkeley, CA 94720-3840, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine a definition of the mutual information of two reals proposed by Levin in [5]. The mutual information is

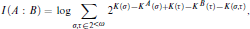
where K(·) is the prefix-free Kolmogorov complexity. A real A is said to have finite self-information if I (A : A) is finite. We give a construction for a perfect Π10 class of reals with this property, which settles some open questions posed by Hirschfeldt and Weber. The construction produces a perfect set of reals with K(σ) ≤+KA (σ) + f (σ) for any given Δ20f with a particularly nice approximation and for a specific choice of f it can also be used to produce a perfect Π10 set of reals that are low for effective Hausdorff dimension and effective packing dimension. The construction can be further adapted to produce a single perfect set of reals that satisfy K(σ) ≤+KA (σ) + f (σ) for all f in a ‘nice’ class of Δ20 functions which includes all Δ20 orders.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 4 , December 2013 , pp. 1229 - 1246
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Athreya, Krishna B., Hitchcock, John M., Lutz, Jack H., and Mayordomo, Elvira, Effective strong dimension in algorithmic information and computational complexity, STACS 2004 (Diekert, V. and Habib, M., editors), Lecture Notes in Computer Science, vol. 2996, Springer, 2004, pp. 632–643.Google Scholar
[2] Downey, Rodney G. and Hirschfeldt, Denis R., Algorithmic randomness and complexity, Theory and Applications of Computability, Springer, 2010.Google Scholar
[3] Hirschfeldt, Denis R. and Weber, Rebecca, Finite self-information, Computability, vol. 1 (2012), no. 1, pp. 85–98.CrossRefGoogle Scholar
[4] Lempp, Steffen, Miller, Joseph S., Ng, Keng Meng, Turetsky, Daniel, and Weber, Rebecca, Lowness for effective Hausdorff dimension, to appear.Google Scholar
[5] Levin, L. A., Laws on the conservation (zero increase) of information, and questions on the foundations of probability theory, Problemy Peredači Informacii, vol. 10 (1974), no. 3, pp. 30–35.Google Scholar
[6] Mayordomo, Elvira, A Kolmogorov complexity characterization of constructive Hausdorff dimension, Information Processing Letters, vol. 84 (2002), no. 1, pp. 1–3.CrossRefGoogle Scholar
[7] André Nies, , Lowness properties and randomness, Advances in Mathematics, vol. 197 (2005), no. 1, pp. 274–305.Google Scholar
[8] André Nies, , Computability and randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.Google Scholar