Orthogonal families of real sequences

Extract

For x, y ϵ ℝ^ω define the inner product

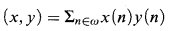
which may not be finite or even exist. We say that x and y are orthogonal if (x, y) converges and equals 0.

Define l_p to be the set of all x ϵ ℝ^ω such that

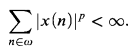
For Hilbert space, l₂, any family of pairwise orthogonal sequences must be countable. For a good introduction to Hilbert space, see Retherford [4].

Theorem 1. There exists a pairwise orthogonal family F of size continuum such that F is a subset of l_p for every p > 2.

It was already known that there exists a family of continuum many pairwise orthogonal elements of ℝ^ω. A family F ⊆ ℝ^ω∖0 of pairwise orthogonal sequences is orthogonally complete or a maximal orthogonal family iff the only element of ℝ^ω orthogonal to every element of F is 0, the constant 0 sequence.

It is somewhat surprising that Kunen's perfect set of orthogonal elements is maximal (a fact first asserted by Abian). MAD families, nonprincipal ultrafilters, and many other such maximal objects cannot be even Borel.

Theorem 2. There exists a perfect maximal orthogonal family of elements of ℝ^ω.

Abian raised the question of what are the possible cardinalities of maximal orthogonal families.

Theorem 3. In the Cohen real model there is a maximal orthogonal set in ℝ^ω of cardinality ω₁, but there is no maximal orthogonal set of cardinality κ with ω₁ < κ < ϲ.

By the Cohen real model we mean any model obtained by forcing with finite partial functions from γ to 2, where the ground model satisfies GCH and γ^ω = γ.