Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T23:52:06.823Z Has data issue: false hasContentIssue false
  • English
  • Français

On the intuitionistic strength of monotone inductive definitions

Published online by Cambridge University Press:  12 March 2014

Sergei Tupailo
Sergei Tupailo*
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, England, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

We prove here that the intuitionistic theory T0↾ + UMIDN. or even EETJ↾ + UMIDN, of Explicit Mathematics has the strength of 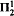–CA0. In Section 1 we give a double-negation translation for the classical second-order μ-calculus, which was shown in [Mö02] to have the strength of 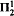–CA0. In Section 2 we interpret the intuitionistic μ-calculus in the theory EETJ↾ + UMIDN. The question about the strength of monotone inductive definitions in T0 was asked by S. Feferman in 1982, and — assuming classical logic — was addressed by M. Rathjen.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 3 , September 2004 , pp. 790 - 798
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Fef75]Feferman, S., A language and axioms for explicit mathematics, Algebra and logic, Lecture Notes in Mathematics, vol. 450, Springer, 1975, pp. 87–139.CrossRefGoogle Scholar
[Fef79]Feferman, S., Constructive theories of functions and classes, Logic colloquium ’78 (Crossley, J. N., editor), North-Holland, 1979. pp. 159–224.Google Scholar
[Fef82]Feferman, S., Monotone inductive definitions, The L. E. J. Brouwer centenary symposium (Troelstra, A. S. and van Dallen, D., editors), North-Holland, Amsterdam, 1982, pp. 77–89.Google Scholar
[GRS97]Glaß, T., Rathjen, M., and Schlüter, A., On the proof-theoretic strength of monotone induction in explicit mathematics, Annals of Pure and Applied Logic, vol. 85 (1997), pp. 1–46.CrossRefGoogle Scholar
[Mö02]Möllerfeld, M., Generalized Inductive Definitions. The μ-calculus and -comprehension, Ph.D. thesis, Universität Münster, 2002.Google Scholar
[Ra96]Rathjen, M., Monotone inductive definitions in explicit mathematics, this Journal, vol. 61 (1996), pp. 125–146.Google Scholar
[Ra98]Rathjen, M., Explicit mathematics with the monotone fixed point principle, this Journal, vol. 63 (1998), pp. 509–542.Google Scholar
[Ra99]Rathjen, M., Explicit mathematics with the monotone fixed point principle. II. Models, this Journal, vol. 64 (1999), pp. 517–550.Google Scholar
[Ra02]Rathjen, M., Explicit mathematics with monotone inductive definitions: a survey, Reflections on the foundations of mathematics: Essays in Honour of Solomon Feferman (Sieg, W.et al., editors). Lecture Notes in Logic, vol. 15, Association of Symbolic Logic, 2002, pp. 329–346.Google Scholar
[Tak89]Takahashi, S., Monotone inductive definitions in a constructive theory of functions and classes, Annals of Pure and Applied Logic, vol. 42 (1989), pp. 255–297.CrossRefGoogle Scholar
[Tu03]Tupailo, S., Realization of constructive set theory into Explicit Mathematics: a lower bound for impredicative Mahlo universe, Annals of Pure and Applied Logic, vol. 120 (2003), no. 1–3, pp. 165–196.CrossRefGoogle Scholar