On the compactness of some Boolean algebras

Extract

We say that the Boolean algebra B is λ-compact, where λ is a cardinal number, if for every family Z ⊆ B∖{0} of power at most λ, if inf Z = 0 then for some finite subfamily Z₀ ⊆ Z we have inf Z₀ = 0.

On the set of all finite subsets of a cardinal number κ, which is denoted [κ]^<ω, the sets of the form 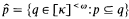for any p Є [κ]^<ω generate the filter T_κ.

This filter is a standard example of a κ-regular filter (see [2]). Because of the importance of κ-regular filters in studying the saturatedness of ultraproducts and reduced products by model-theoretic methods, the question of compactness of the algebra B_κ = P([κ]^<ω/T_κ was natural. This question in the most optimistical way was formulated by M. Benda [1, Problem 5c]: is the algebra B_κω-compact for every uncountable κ?

In this paper we show that for most of the cardinal numbers which are greater or equal to 2^ω the algebra B_κ is not ω-compact. Hence, in view of obtained results, the following question appears: does there exist an uncountable κ such that the algebra B_κ is κ-compact?

We use standard set-theoretical notations. CH denotes the Continuum Hypothesis, GCH denotes the General Continuum Hypothesis and MA denotes Martin's Axiom.