Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T01:28:09.075Z Has data issue: false hasContentIssue false
  • English
  • Français

On finite approximations of topological algebraic systems

Published online by Cambridge University Press:  12 March 2014

L. Yu. Glebsky ,
E. I. Gordon  and
C. Ward Henson
L. Yu. Glebsky
Affiliation:
Universidad Autonoma de San Luis Potosi, Instituto de Investigacion en Communicacion Optica, Avkarakorum 1470, Lomas 4TA Session, San Luis Potosi SLP 7820, Mexico. E-mail: [email protected]
E. I. Gordon
Affiliation:
Eastern Illinois University, Department of Mathematics and Computer Science, 600 Lincoln Avenue, Charleston, IL 61920-3099, USA. E-mail: [email protected]
C. Ward Henson
Affiliation:
University of Illinois at Urbana-Champaign, Department of Mathematics, 1409 West Green Street, Urbana, IL 61801, USA. E-mail: [email protected] URL: http://www.math.uiuc.edu/˜henson
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce and discuss a concept of approximation of a topological algebraic system A by finite algebraic systems from a given class 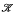. If A is discrete, this concept agrees with the familiar notion of a local embedding of A in a class 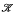of algebraic systems. One characterization of this concept states that A is locally embedded in 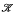iff it is a subsystem of an ultraproduct of systems from 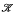. In this paper we obtain a similar characterization of approximability of a locally compact system A by systems from using the language of nonstandard analysis.

In the signature of A we introduce positive bounded formulas and their approximations; these are similar to those introduced by Henson [14] for Banach space structures (see also [15, 16]). We prove that a positive bounded formula φ holds in A if and only if all precise enough approximations of φ hold in all precise enough approximations of A.

We also prove that a locally compact field cannot be approximated arbitrarily closely by finite (associative) rings (even if the rings are allowed to be non-commutative). Finite approximations of the field ℝ can be considered as possible computer systems for real arithmetic. Thus, our results show that there do not exist arbitrarily accurate computer arithmetics for the reals that are associative rings.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 1 - 25
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Albeverio, S., Gordon, E., and Khrennikov, A., Finite dimensional approximations of operators in the spaces of functions on locally compact abelian groups, Acta Applicandae Mathematical, vol. 64 (2000), pp. 64–2000.CrossRefGoogle Scholar
[2]Alekseev, M. A., Glebskii, L. Y., and Gordon, E. I., On approximations of groups, group actions and Hopf algebras, Representation Theory, Dynamical Systems, Combinatorial and Algebraic Methods, III (Vershik, A. M., editor), Russian Academy of Science, St. Petersburg Branch of V. A. Steklov's Mathematical Institute, Zapiski nauchnih seminarov POMI 256, 1999, pp. 224–262, (in Russian), English translation in Journal of Mathematical Sciences, vol. 107 (2001), pp. 4305–4332.Google Scholar
[3]Andreev, P. V. and Gordon, E. I., A theory of hyperfinite sets, Annals of Pure and Applied Logic, to appear.Google Scholar
[4]Bourbaki, N., General Topology, Part 1, Hermann, Paris and Addison-Wesley, Reading, Massachusetts, 1966.Google Scholar
[5]Chang, C. C. and Keisler, H. J., Model Theory, 3rd ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland Elsevier, Amsterdam, 1990.Google Scholar
[6]Digernes, T., Husstad, E., and Varadarajan, V., Finite approximations of Weyl systems, Mathematica Scandinavicae, vol. 84 (1999), pp. 84–1999.Google Scholar
[7]Glebsky, L. Y. and Gordon, E. I., On approximation of topological groups by finite quasigroups and finite semigroups, Illinois Journal of Mathematics, vol. 49 (2005), pp. 49–2005.Google Scholar
[8]Goldblatt, R., Lectures on the Hyperreals: An Introduction to Nonstandard Analysis, Springer-Verlag, Berlin, Heidelberg, New York, 1998.CrossRefGoogle Scholar
[9]Gordon, E. I., Nonstandard analysis and locally compact abelian groups, Acta Applicandae Mathematicae, vol. 25 (1991), pp. 25–1991.CrossRefGoogle Scholar
[10]Gordon, E. I., Nonstandard Methods in Commutative Harmonic Analysis, American Mathematical Society, Providence, Rhode Island, 1997.CrossRefGoogle Scholar
[11]Gordon, E. I., Kusraev, A. G., and Kutateladze, S. S., Infinitesimal Analysis, Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.CrossRefGoogle Scholar
[12]Gordon, E. I. and Rezvova, O. A., On hyperfinite approximations of the field ℝ, Reuniting the antipodes — Constructive and nonstandard views of the continuum, Proceedings of the Symposium in San Servolo/Venice, Italy, May 17–20, 2000 (Schuster, P., Berger, U., and Osswald, H. H., editors), Synthése Library, vol. 306, Kluwer Academic Publishers, Dordrecht, Boston, London, 2001.Google Scholar
[13]Heinrich, S. and Henson, C. W., Banach space model theory II; Isomorphic equivalence, Mathematische Nachrichten, vol. 125 (1986), pp. 125–1986.CrossRefGoogle Scholar
[14]Henson, C. W., Nonstandard hulls of Banach spaces, Israel Journal of Mathematics, vol. 25 (1976), pp. 25–1976.CrossRefGoogle Scholar
[15]Henson, C. W. and Iovino, J., Ultraproducts in analysis. Analysis and Logic (Finet, C. and Michaux, C., editors), London Mathematical Society Lecture Notes, vol. 262, Cambridge University Press, 2002, pp. 1–113.Google Scholar
[16]Henson, C. W. and Moore, L.C., Nonstandard analysis and the theory of Banach spaces, Nonstandard Analysis — Recent Developments (Hurd, A., editor), Lecture Notes in Mathematics, vol. 983, Springer-Verlag, Berlin, Heidelberg, New York, 1983.Google Scholar
[17]Knuth, D., The Art of Computer Programming; Volume 2, Seminumerical Algorithms, Addison Wesley, Reading, Massachusetts, 1969.Google Scholar
[18]Loeb, P. and Wolff, M. (editors), Nonstandard Analysis for the Working Mathematician, Kluwer Academic Publishers, Dordrecht, Boston, London, 2000.CrossRefGoogle Scholar
[19]Loomis, L., An Introduction to Abstract Harmonic Analysis, D. Van Nostrand, Toronto, New York, London, 1953.Google Scholar
[20]Mal'tsev, A. I., Algebraic Systems, Nauka, Moscow, 1970, in Russian.Google Scholar
[21]McCracken, D. D. and Dorn, W. S., Numerical Methods and Fortran Programming, John Wiley, New York, London, Sydney, 1964.Google Scholar
[22]Nelson, E., Internal set theory – A new approach to nonstandard analysis, Bulletin of the American Mathematical Society, vol. 83 (1977), pp. 83–1977.CrossRefGoogle Scholar
[23]Nelson, E., The syntax of nonstandard analysis, Annals of Pure and Applied Logic, vol. 38 (1988), pp. 38–1988.CrossRefGoogle Scholar
[24]Tarski, A., A Decision Method for Elementary Algebra and Geometry, 2nd, revised ed., Rand Corporation, Berkeley and Los Angeles, 1951.CrossRefGoogle Scholar
[25]Vershik, A. M. and Gordon, E. I., Groups that are locally embedded into the class of finite groups, Algebra i Analiz, vol. 9 (1997), pp. 71–97, English translation as: St. Petersburg Mathematics Journal, vol. 9 (1997), pp. 49–67.Google Scholar
[26]Vopěnka, P., Mathematics in the Alternative Set Theory, Teubner, Leipzig, 1979.Google Scholar
[27]Zeilberger, D., Real analysis is a degenerate case of discrete analysis, New Progress in Difference Equations, Proc. ICDEA'01 (Aulbach, B., Elyadi, S., and Ladas, G., editors), Taylor and Frances, London, 2001.Google Scholar