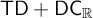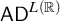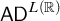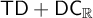1. Introduction
There are two known proofs that
![]() $\mathsf {TD}+\mathsf {DC}_{\mathbb {R}}$
imply
$\mathsf {TD}+\mathsf {DC}_{\mathbb {R}}$
imply
![]() $\mathsf {AD}^{L(\mathbb {R})}$
both due to Woodin. The later proof involves proving the stronger result of Suslin determinacy from Turing determinacy +
$\mathsf {AD}^{L(\mathbb {R})}$
both due to Woodin. The later proof involves proving the stronger result of Suslin determinacy from Turing determinacy +
![]() $\mathsf {DC}_{\mathbb {R}}$
directly [Reference Hugh Woodin1]. Combining that with Kechris and Woodin’s theorem that Suslin determinacy in
$\mathsf {DC}_{\mathbb {R}}$
directly [Reference Hugh Woodin1]. Combining that with Kechris and Woodin’s theorem that Suslin determinacy in
![]() $L(\mathbb {R})$
implies
$L(\mathbb {R})$
implies
![]() $\mathsf {AD}^{L(\mathbb {R})}$
[Reference Kechris and Hugh Woodin2], the desired result becomes an immediate corollary.
$\mathsf {AD}^{L(\mathbb {R})}$
[Reference Kechris and Hugh Woodin2], the desired result becomes an immediate corollary.
Woodin’s original proof uses an early version of the core model induction (CMI) technique. Through the work of many set theorists, the CMI has been developed into a proper framework for proving determinacy results from non-large cardinal hypotheses such as generic elementary embeddings, forcing axioms, and the failure of fine-structural combinatorial principles. The technique as it is understood in
![]() $L(\mathbb {R})$
-like models (i.e.,
$L(\mathbb {R})$
-like models (i.e.,
![]() $L(\mathbb {R}^g)$
where
$L(\mathbb {R}^g)$
where
![]() $\mathbb {R}^g$
are the reals of a symmetric collapse) can be seen as an inductive method by which one proves
$\mathbb {R}^g$
are the reals of a symmetric collapse) can be seen as an inductive method by which one proves
![]() $J_\alpha (\mathbb {R})\models \mathsf {AD}$
for all
$J_\alpha (\mathbb {R})\models \mathsf {AD}$
for all
![]() $\alpha $
. An introduction to this as well as all terminology used in this paper can be found in Schindler and Steel’s book [Reference Schindler and Steel7].
$\alpha $
. An introduction to this as well as all terminology used in this paper can be found in Schindler and Steel’s book [Reference Schindler and Steel7].
This paper aims to prove that
![]() $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$
implies
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$
implies
![]() $\mathsf {AD}^{L(\mathbb {R})}$
using modern perspectives on the core model induction in
$\mathsf {AD}^{L(\mathbb {R})}$
using modern perspectives on the core model induction in
![]() $L(\mathbb {R})$
. The key lemma is a modification of a well-known theorem of Kechris and Solovay to work in the
$L(\mathbb {R})$
. The key lemma is a modification of a well-known theorem of Kechris and Solovay to work in the
![]() $\mathsf {TD}$
context. Utilizing the proof of the witness dichotomy it is sufficient to just prove the
$\mathsf {TD}$
context. Utilizing the proof of the witness dichotomy it is sufficient to just prove the
![]() $J\mapsto M_1^{\#,J}$
step of the core model induction.
$J\mapsto M_1^{\#,J}$
step of the core model induction.
2. Rough background
2.1. Determinacy
Given some
![]() $A\subseteq \omega ^\omega $
the Gale–Stewart game
$A\subseteq \omega ^\omega $
the Gale–Stewart game
![]() $G_\omega (A)$
is defined to be the perfect information game where two players
$G_\omega (A)$
is defined to be the perfect information game where two players
![]() $\mathbf {I}$
and
$\mathbf {I}$
and
![]() $\mathbf {II}$
take turns playing digits
$\mathbf {II}$
take turns playing digits
![]() $x_n\in \omega $
for
$x_n\in \omega $
for
![]() $\omega $
turns as written:
$\omega $
turns as written:

This results in the infinite sequence
![]() $x = (x_0,x_1,\ldots )\in \omega ^\omega $
. We say that
$x = (x_0,x_1,\ldots )\in \omega ^\omega $
. We say that
![]() $\mathbf {I}$
wins if
$\mathbf {I}$
wins if
![]() $x\in A$
, otherwise we say
$x\in A$
, otherwise we say
![]() $\mathbf {II}$
wins. A player is said to have a winning strategy provided they can ensure themselves a win regardless of how their opponent plays. A game
$\mathbf {II}$
wins. A player is said to have a winning strategy provided they can ensure themselves a win regardless of how their opponent plays. A game
![]() $G_\omega (A)$
is determined if a player has a winning strategy.
$G_\omega (A)$
is determined if a player has a winning strategy.
Definition 2.1. The axiom of determinacy
![]() $\mathsf {AD}$
states that for every
$\mathsf {AD}$
states that for every
![]() $A\subseteq \omega ^\omega $
,
$A\subseteq \omega ^\omega $
,
![]() $G_\omega (A)$
is determined.
$G_\omega (A)$
is determined.
One of the earliest remarkable consequences of
![]() $\mathsf {AD}$
is Martin’s cone theorem. We say that
$\mathsf {AD}$
is Martin’s cone theorem. We say that
![]() $\mathbf A\subseteq \mathcal D$
is a cone if there is some
$\mathbf A\subseteq \mathcal D$
is a cone if there is some
![]() $\mathbf {x}\in \mathcal D$
such that
$\mathbf {x}\in \mathcal D$
such that
![]() $\mathbf A = \{\mathbf {a}\mid \mathbf {a}\geq _{\mathcal {D}}\mathbf x\}$
.
$\mathbf A = \{\mathbf {a}\mid \mathbf {a}\geq _{\mathcal {D}}\mathbf x\}$
.
Theorem 2.2 [Reference Martin4]
Assume
![]() $\mathsf {AD}$
. Suppose that
$\mathsf {AD}$
. Suppose that
![]() $\mathbf A\subseteq \mathcal D$
. Then either
$\mathbf A\subseteq \mathcal D$
. Then either
![]() $\mathbf A$
or
$\mathbf A$
or
![]() $\mathbf A^c$
contains a Turing cone.
$\mathbf A^c$
contains a Turing cone.
Proof Consider the set
![]() $A = \{x\in \mathbb {R}\mid [x]_T\in \mathbf A\}$
. As this is a set of reals it’s determined, so assume that player I has a winning strategy
$A = \{x\in \mathbb {R}\mid [x]_T\in \mathbf A\}$
. As this is a set of reals it’s determined, so assume that player I has a winning strategy
![]() $\sigma $
. Then for any
$\sigma $
. Then for any
![]() $x\geq _T\sigma $
we have that
$x\geq _T\sigma $
we have that
![]() $x\equiv _T\sigma *x\in A$
. Therefore,
$x\equiv _T\sigma *x\in A$
. Therefore,
![]() $\{x\mid x\geq _T\sigma \}\subseteq A$
and
$\{x\mid x\geq _T\sigma \}\subseteq A$
and
![]() $\{\mathbf x\mid \mathbf x\geq _{\mathcal {D}}[\sigma ]_T\}\subseteq \mathbf A$
. If player II has a winning strategy
$\{\mathbf x\mid \mathbf x\geq _{\mathcal {D}}[\sigma ]_T\}\subseteq \mathbf A$
. If player II has a winning strategy
![]() $\tau $
, then there is an almost identical argument that
$\tau $
, then there is an almost identical argument that
![]() $\mathbf A^c$
contains a Turing cone above
$\mathbf A^c$
contains a Turing cone above
![]() $[\tau ]_T$
.
$[\tau ]_T$
.
The axiom of Turing determinacy (
![]() $\mathsf {TD}$
) is the isolation of the consequence of this theorem, e.g., that every set of Turing degrees contains or is disjoint from a cone.
$\mathsf {TD}$
) is the isolation of the consequence of this theorem, e.g., that every set of Turing degrees contains or is disjoint from a cone.
2.2. Core model theory
The core model theory required in a core model induction is largely summarized by the
![]() $K^J$
existence dichotomy. This is a straightforward generalization of the typical K existence dichotomy to a hierarchy of relativized mice. These relativized mice, called hybrid mice, abstract the use of the rudimentary closure to take a one step in the constructibility hierarchy to the use of some “model operator” J with similar enough properties. Examples of model operators include:
$K^J$
existence dichotomy. This is a straightforward generalization of the typical K existence dichotomy to a hierarchy of relativized mice. These relativized mice, called hybrid mice, abstract the use of the rudimentary closure to take a one step in the constructibility hierarchy to the use of some “model operator” J with similar enough properties. Examples of model operators include:
-
•
 $x\mapsto \text {rud}(x\cup \{x\})$
;
$x\mapsto \text {rud}(x\cup \{x\})$
; -
• Mouse operators, e.g., the sharp operator, the one Woodin cardinal operator;
-
• Hybrid mouse operators, e.g., term-relation hybrid mouse operators from self-justifying systems, strategy hybrid mouse operators.
For an exposition of operator mice in the style of this paper one can read either Chapter 1 of [Reference Schindler and Steel7] or Sections 2.1–2.3 of [Reference Wilson11]. For the sake of this paper, the full definition of a mouse operator is not that important.
An important property all model operators of interest have is that they “condense well.” Condensing well is a technical condition ensuring that one can develop a fine structure for structures built in terms of J, i.e., one can perform background constructions relativized to J that behave in the same manner as they do with the rudimentary closure. In particular, J condensing well implies that the models constructed in a
![]() $K^{c,J}$
construction are J-premice and there is a relativized core model theory.
$K^{c,J}$
construction are J-premice and there is a relativized core model theory.
Theorem 2.3. (
 $K^J$
existence dichotomy)
$K^J$
existence dichotomy)
Let
![]() $\Omega $
be a measurable cardinal. Let J be a model operator with real parameter z on
$\Omega $
be a measurable cardinal. Let J be a model operator with real parameter z on
![]() $H_\Omega $
which condenses well. Let
$H_\Omega $
which condenses well. Let
![]() $\mathcal P$
be countable model with parameter z and let
$\mathcal P$
be countable model with parameter z and let
![]() $K^{c,J}(\mathcal P) = K^{c,J}(\mathcal P)|\Omega $
. Then the following statements are true
$K^{c,J}(\mathcal P) = K^{c,J}(\mathcal P)|\Omega $
. Then the following statements are true
![]() $:$
$:$
-
1. If the
 $K^{c,J}(\mathcal P)$
construction reaches
$K^{c,J}(\mathcal P)$
construction reaches
 $M_1^{\#,J}(\mathcal P)$
, then
$M_1^{\#,J}(\mathcal P)$
, then
 $M_1^{\#,J}(\mathcal P)$
is
$M_1^{\#,J}(\mathcal P)$
is
 $(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
$(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
 $J^\#$
, i.e., the sharp for
$J^\#$
, i.e., the sharp for
 $L^{J}$
.
$L^{J}$
. -
2. If the
 $K^{c,J}(\mathcal P)$
construction does not reach
$K^{c,J}(\mathcal P)$
construction does not reach
 $M_1^{\#,J}(\mathcal P)$
, then
$M_1^{\#,J}(\mathcal P)$
, then
 $K^{c,J}(\mathcal P)$
is
$K^{c,J}(\mathcal P)$
is
 $(\omega ,\Omega , \Omega +1)$
-iterable. This implies that
$(\omega ,\Omega , \Omega +1)$
-iterable. This implies that
 $K^J(\mathcal P)$
exists and is
$K^J(\mathcal P)$
exists and is
 $(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
$(\omega ,\Omega ,\Omega +1)$
-iterable via the unique strategy guided by
 $J^\#$
.
$J^\#$
.
In this case, the “true”
![]() $K^J(\mathcal P)$
is defined as in [Reference Steel9], the only real change being that one has to relativize all notions considered there to the model operator J.
$K^J(\mathcal P)$
is defined as in [Reference Steel9], the only real change being that one has to relativize all notions considered there to the model operator J.
All model operators encountered in the core model induction condense well. Additional properties possessed by all model operators encountered in the core model induction are that they relativize well and determine themselves on generic extensions.
Definition 2.4. We say that a model operator J relativizes well if there is a formula
![]() $\varphi (x,y,z)$
such that for any
$\varphi (x,y,z)$
such that for any
![]() $\mathcal N,\mathcal N'$
models such that
$\mathcal N,\mathcal N'$
models such that
![]() $\mathcal N\in |\mathcal N'|$
and
$\mathcal N\in |\mathcal N'|$
and
![]() $\mathcal {M}$
a J-premouse with base model
$\mathcal {M}$
a J-premouse with base model
![]() $\mathcal N'$
such that
$\mathcal N'$
such that
![]() $\mathcal {M}\models \mathsf {ZFC}^-$
, then
$\mathcal {M}\models \mathsf {ZFC}^-$
, then
![]() $J(\mathcal N)\in \mathcal M$
and
$J(\mathcal N)\in \mathcal M$
and
![]() $J(\mathcal N)$
is the unique
$J(\mathcal N)$
is the unique
![]() $x\in |\mathcal M|$
such that
$x\in |\mathcal M|$
such that
![]() $\varphi (x,\mathcal N,J(\mathcal N'))$
.
$\varphi (x,\mathcal N,J(\mathcal N'))$
.
Definition 2.5. We say that J determines itself on generic extensions if there is a formula
![]() $\phi (x,y,z)$
and some parameter
$\phi (x,y,z)$
and some parameter
![]() $c\in HC$
such that for any countable transitive structure
$c\in HC$
such that for any countable transitive structure
![]() $\mathcal M$
satisfying
$\mathcal M$
satisfying
![]() $\mathsf {ZFC}^-$
containing c and closed under J, for any generic extension
$\mathsf {ZFC}^-$
containing c and closed under J, for any generic extension
![]() $\mathcal M[g]$
of
$\mathcal M[g]$
of
![]() $\mathcal M$
in V,
$\mathcal M$
in V,
![]() $J\cap \mathcal M[g]\in M[g]$
and is definable via
$J\cap \mathcal M[g]\in M[g]$
and is definable via
![]() $b = J(a)$
iff
$b = J(a)$
iff
![]() $\mathcal M[g]\models \phi (c,a,b)$
.
$\mathcal M[g]\models \phi (c,a,b)$
.
3. Kechris–Solovay theorem
The following is our primary lemma which is a modification on a theorem of Kechris and Solovay [Reference Kechris and Solovay3]. Given a set of ordinals S,
![]() $\mathsf {OD}_S$
-Turing determinacy (i.e.,
$\mathsf {OD}_S$
-Turing determinacy (i.e.,
![]() $\mathsf {OD}_S$
-
$\mathsf {OD}_S$
-
![]() $\mathsf {TD}$
) is the assertion that every set of Turing degrees ordinal definable with S as an additional parameter contains or is disjoint from a Turing cone.
$\mathsf {TD}$
) is the assertion that every set of Turing degrees ordinal definable with S as an additional parameter contains or is disjoint from a Turing cone.
Lemma 3.1. Assume
![]() $\mathsf {\mathsf {TD}}$
. For any set of ordinals S, on a Turing cone
$\mathsf {\mathsf {TD}}$
. For any set of ordinals S, on a Turing cone
![]() $\mathcal C$
the following holds for
$\mathcal C$
the following holds for
![]() $x\in \mathcal C$
:
$x\in \mathcal C$
:
Proof Assume for a contradiction that there is no cone of reals on which
![]() $L[S,x]\models \mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
. Then we can define, on a cone
$L[S,x]\models \mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
. Then we can define, on a cone
![]() $\mathcal C$
, the map
$\mathcal C$
, the map
![]() $x\mapsto A_x$
where
$x\mapsto A_x$
where
![]() $A_x$
is the least
$A_x$
is the least
![]() $\mathsf {OD}_{S}^{L[S,x]} \equiv _T$
-invariant subset of
$\mathsf {OD}_{S}^{L[S,x]} \equiv _T$
-invariant subset of
![]() $\mathbb R$
which doesn’t contain a Turing cone and whose complement does not contain a Turing cone in
$\mathbb R$
which doesn’t contain a Turing cone and whose complement does not contain a Turing cone in
![]() $L[S,x]$
. Notice that
$L[S,x]$
. Notice that
![]() $A_x$
only depends on the S-constructibility degree of x.
$A_x$
only depends on the S-constructibility degree of x.
It is clear from the last observation that the set
![]() $\{x\in \mathbb R\mid x\in A_x\}$
is
$\{x\in \mathbb R\mid x\in A_x\}$
is
![]() $\equiv _T$
-invariant and is well-defined on
$\equiv _T$
-invariant and is well-defined on
![]() $\mathcal C$
. Suppose that this set contains a Turing cone
$\mathcal C$
. Suppose that this set contains a Turing cone
![]() $\mathcal C'$
. Consider some arbitrary
$\mathcal C'$
. Consider some arbitrary
![]() $y\in \mathcal C\cap \mathcal C'$
, if
$y\in \mathcal C\cap \mathcal C'$
, if
![]() $w\geq _{T} z\geq _{T} y$
and
$w\geq _{T} z\geq _{T} y$
and
![]() $w\in L[S,z]$
then we have that
$w\in L[S,z]$
then we have that
![]() $w\in A_w = A_z$
. So
$w\in A_w = A_z$
. So
![]() $A_z$
contains a Turing cone in
$A_z$
contains a Turing cone in
![]() $L[S,z]$
. We reach a similar conclusion if we assume that
$L[S,z]$
. We reach a similar conclusion if we assume that
![]() $\{x\in \mathbb R\mid x\not \in A_x\}$
contains a Turing cone. Contradiction.
$\{x\in \mathbb R\mid x\not \in A_x\}$
contains a Turing cone. Contradiction.
Ordinal (Turing) determinacy has the following well-known consequence:
Corollary 3.2.
![]() $\mathsf {\mathsf {HOD}}_{{S}}^{L[S,x]}\models \text {" }\omega _1^{L[S,x]}\text { is measurable"}$
for a cone of x.
$\mathsf {\mathsf {HOD}}_{{S}}^{L[S,x]}\models \text {" }\omega _1^{L[S,x]}\text { is measurable"}$
for a cone of x.
Proof outline
This proof is standard, but for the sake of completeness it will be sketched. We work inside
![]() $L[S,x]$
and assume that
$L[S,x]$
and assume that
![]() $\mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
holds. Let f be the function
$\mathsf {OD}_{S}\text {-}\mathsf {\mathsf {TD}}$
holds. Let f be the function
![]() $f : x\mapsto \omega _1^x$
which maps x to the least x-admissible ordinal, then we can define
$f : x\mapsto \omega _1^x$
which maps x to the least x-admissible ordinal, then we can define
![]() $\mu $
as the pushforward of the cone filter under f, i.e.,
$\mu $
as the pushforward of the cone filter under f, i.e.,
![]() $A\in \mu $
iff
$A\in \mu $
iff
![]() $f^{-1}(A)\text { contains a Turing cone}$
. Clearly
$f^{-1}(A)\text { contains a Turing cone}$
. Clearly
![]() $\mu $
is countably closed and, by assumption,
$\mu $
is countably closed and, by assumption,
![]() $\mu $
restricts to an ultrafilter on
$\mu $
restricts to an ultrafilter on
![]() $P(\omega _1)\cap \mathsf {OD}_S$
. The cone measure and the map f are both definable, so
$P(\omega _1)\cap \mathsf {OD}_S$
. The cone measure and the map f are both definable, so
![]() $\mathsf {\mathsf {HOD}}_{S}\cap \mu \in \mathsf {\mathsf {HOD}}_{S}$
witnesses that
$\mathsf {\mathsf {HOD}}_{S}\cap \mu \in \mathsf {\mathsf {HOD}}_{S}$
witnesses that
![]() $\omega _1^{V}$
is measurable in
$\omega _1^{V}$
is measurable in
![]() $\mathsf {\mathsf {HOD}}_S$
.
$\mathsf {\mathsf {HOD}}_S$
.
4. The existence of
 $M_1^\#$
$M_1^\#$
The following consequences of
![]() $\Delta ^1_2$
-
$\Delta ^1_2$
-
![]() $\mathsf {\mathsf {TD}}$
are proven by modifying the analogous arguments from
$\mathsf {\mathsf {TD}}$
are proven by modifying the analogous arguments from
![]() $\Delta ^1_2$
-
$\Delta ^1_2$
-
![]() $\mathsf {Det}$
in a similar fashion to the core argument of Theorem 3.1 then verifying that nothing breaks. As the modifications are relatively straightforward the proofs will not be included.
$\mathsf {Det}$
in a similar fashion to the core argument of Theorem 3.1 then verifying that nothing breaks. As the modifications are relatively straightforward the proofs will not be included.
-
• (Martin) Assume
 $\Delta ^1_2$
-
$\Delta ^1_2$
-
 $\mathsf {TD + DC}$
, then
$\mathsf {TD + DC}$
, then
 $\Pi ^1_2\text {-}\mathsf {\mathsf {TD}}$
.
$\Pi ^1_2\text {-}\mathsf {\mathsf {TD}}$
. -
• (Kechris–Solovay) Assume
 $\Delta ^1_2$
-
$\Delta ^1_2$
-
 $\mathsf {TD + DC}$
, then for any real y, on a Turing cone
$\mathsf {TD + DC}$
, then for any real y, on a Turing cone
 $x\in \mathcal C$
the following holds for
$x\in \mathcal C$
the following holds for
 $x\in \mathcal C$
:
$x\in \mathcal C$
:  $$ \begin{align*}L[x,y]\models\mathsf{OD}_{{y}}\text{-}\mathsf{TD}.\end{align*} $$
$$ \begin{align*}L[x,y]\models\mathsf{OD}_{{y}}\text{-}\mathsf{TD}.\end{align*} $$
-
• (Consequence of Kechris–Woodin [Reference Kechris and Hugh Woodin2]) Assume
 $\Delta ^1_2$
-
$\Delta ^1_2$
-
 $\mathsf {TD {\kern-1pt}+{\kern-1pt} DC}$
and
$\mathsf {TD {\kern-1pt}+{\kern-1pt} DC}$
and
 $(\forall x{\kern-1pt}\in{\kern-1pt} \mathbb {R}) x^\#\text { exists}$
, then
$(\forall x{\kern-1pt}\in{\kern-1pt} \mathbb {R}) x^\#\text { exists}$
, then
 $\operatorname {Th}(L[x])$
is fixed on a Turing cone.
$\operatorname {Th}(L[x])$
is fixed on a Turing cone.
We can utilize these three observations to prove the first step in our induction from a weaker hypothesis.
Theorem 4.1. Assume
![]() $\Delta ^1_2$
-
$\Delta ^1_2$
-
![]() $\mathsf {TD + DC}$
and
$\mathsf {TD + DC}$
and
![]() $(\forall x\in \mathbb {R})\: x^\#\text { exists}$
, then
$(\forall x\in \mathbb {R})\: x^\#\text { exists}$
, then
![]() $M_1^\#$
exists and is
$M_1^\#$
exists and is
![]() $\omega _1$
-iterable.
$\omega _1$
-iterable.
Proof Utilizing lemma 3.1 we have that
![]() $L[x]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
on a Turing cone. Let x be the base of such a cone and fix the least x-indiscernible
$L[x]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
on a Turing cone. Let x be the base of such a cone and fix the least x-indiscernible
![]() $i^x_0 < \omega _1^V$
. The measure U on
$i^x_0 < \omega _1^V$
. The measure U on
![]() $i^x_0$
given by
$i^x_0$
given by
![]() $x^\#$
is sufficient for the construction of the Steel core model K (as described in CMIP [Reference Steel9]) in
$x^\#$
is sufficient for the construction of the Steel core model K (as described in CMIP [Reference Steel9]) in
![]() $L[x]$
below
$L[x]$
below
![]() $i^x_0$
. Suppose that the
$i^x_0$
. Suppose that the
![]() $K^c$
construction below
$K^c$
construction below
![]() $i^x_0$
in
$i^x_0$
in
![]() $L[x]$
does not reach an
$L[x]$
does not reach an
![]() $M_1$
-like premouse, then there is a U-measure one set of
$M_1$
-like premouse, then there is a U-measure one set of
![]() $\alpha < i_0$
we have that
$\alpha < i_0$
we have that
![]() $L[x]\models (\alpha ^+)^K = \alpha ^+$
. Select such an
$L[x]\models (\alpha ^+)^K = \alpha ^+$
. Select such an
![]() $\alpha $
and let
$\alpha $
and let
![]() $z = \left <x,g\right>$
where g is
$z = \left <x,g\right>$
where g is
![]() $L[x]$
-generic for
$L[x]$
-generic for
![]() $Coll(\omega ,\alpha )$
. Working in
$Coll(\omega ,\alpha )$
. Working in
![]() $L[z]$
, K exists, is inductively definable, and
$L[z]$
, K exists, is inductively definable, and
![]() $\omega _1$
is a successor cardinal in K. As
$\omega _1$
is a successor cardinal in K. As
![]() $z\geq _T x$
we have that
$z\geq _T x$
we have that
![]() $L[z]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
; therefore,
$L[z]\models \mathsf {OD}\text {-}\mathsf {\mathsf {TD}}$
; therefore,
![]() $HOD^{L[z]}\models \omega _1\text { is measurable}$
. But as
$HOD^{L[z]}\models \omega _1\text { is measurable}$
. But as
![]() $K^{L[z]}\subseteq HOD^{L[z]}$
we have a contradiction. Therefore we have that the
$K^{L[z]}\subseteq HOD^{L[z]}$
we have a contradiction. Therefore we have that the
![]() $K^c$
construction of
$K^c$
construction of
![]() $L[x]$
below
$L[x]$
below
![]() $i^x_0$
reaches an
$i^x_0$
reaches an
![]() $M_1$
-like premouse on a cone.
$M_1$
-like premouse on a cone.
Utilizing the limit branch construction described in Theorem 4.16 of HOD as a Core Model [Reference Steel and Hugh Woodin10] there is an
![]() $\omega _1$
-iterable
$\omega _1$
-iterable
![]() $M_1^{\#}$
.
$M_1^{\#}$
.
Note that by [Reference Neeman5], the
![]() $\omega _1$
-iterability of
$\omega _1$
-iterability of
![]() $M_1^\#$
is enough to prove
$M_1^\#$
is enough to prove
![]() $\Delta ^1_2$
-determinacy. So in fact we get an equivalence of
$\Delta ^1_2$
-determinacy. So in fact we get an equivalence of
![]() $\Delta ^1_2\text{-}\mathsf {TD}$
and
$\Delta ^1_2\text{-}\mathsf {TD}$
and
![]() $\Delta ^1_2$
-determinacy under
$\Delta ^1_2$
-determinacy under
![]() $\mathsf {ZF+DC}$
.
$\mathsf {ZF+DC}$
.
5. The
 $J\mapsto M^{\#,J}_1$
step
$J\mapsto M^{\#,J}_1$
step
Following this point on the argument is identical to that of Steel and Schindler. But I will rewrite it (practically verbatim) for the sake of completeness. For the rest of this argument we will assume
![]() $\mathsf {ZF} + \mathsf {TD} + \mathsf {DC} + V = L(\mathbb {R})$
. Recall that every (hybrid) model operator considered in the core model induction relativizes well and determines itself on generic extensions.
$\mathsf {ZF} + \mathsf {TD} + \mathsf {DC} + V = L(\mathbb {R})$
. Recall that every (hybrid) model operator considered in the core model induction relativizes well and determines itself on generic extensions.
Theorem 5.1. Let
![]() $a\in \mathbb {R}$
and let J be a (hybrid) model operator that condenses well, relativizes well, and determines itself on generic extensions, and suppose that
$a\in \mathbb {R}$
and let J be a (hybrid) model operator that condenses well, relativizes well, and determines itself on generic extensions, and suppose that
constructed with height
![]() $\omega _1^V$
exists for a cone of x. Then there is a cone of x such that
$\omega _1^V$
exists for a cone of x. Then there is a cone of x such that
![]() $W_x$
cannot be
$W_x$
cannot be
![]() $\omega _1^V+1$
iterable above a inside
$\omega _1^V+1$
iterable above a inside
![]() $\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}$
.
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}$
.
Proof Assume for a contradiction that this is not the case. Then there is a cone
![]() $\mathcal {C}$
such that for all
$\mathcal {C}$
such that for all
![]() $x\in \mathcal C$
we have
$x\in \mathcal C$
we have
![]() $L^{J^{\#}}[a,x] = L^{J^{\#}}[x]$
and
$L^{J^{\#}}[a,x] = L^{J^{\#}}[x]$
and
and so we can isolate
![]() $K^{J}_x = \left (K^{ J}(a)\right )^{\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}}$
. Furthermore, we can assume that any element of
$K^{J}_x = \left (K^{ J}(a)\right )^{\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[x]}}$
. Furthermore, we can assume that any element of
![]() $\mathcal {C}$
can compute the code for the parameter c which witnesses that J determines itself on generic extensions. Fixing some
$\mathcal {C}$
can compute the code for the parameter c which witnesses that J determines itself on generic extensions. Fixing some
![]() $x\in \mathcal C$
we will write
$x\in \mathcal C$
we will write
![]() $K^{ J}$
for
$K^{ J}$
for
![]() $K^{ J}_x$
.
$K^{ J}_x$
.
Claim 5.2. The universe of
![]() $L^{J^{\#}}[x]$
is a size
$L^{J^{\#}}[x]$
is a size
![]() ${<}{\omega}_1^V$
forcing extension of
${<}{\omega}_1^V$
forcing extension of
![]() $\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
.
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
.
Proof The observation we want to make is that
![]() $L^{J^{\#}}[x]$
is the result of adding x to
$L^{J^{\#}}[x]$
is the result of adding x to
![]() $\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
via Vopenka forcing. Suppose that
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
via Vopenka forcing. Suppose that
![]() $\mathbb {V}$
is the Vopenka forcing and
$\mathbb {V}$
is the Vopenka forcing and
![]() $\tau $
is a name for x, then as
$\tau $
is a name for x, then as
![]() $\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is
![]() $J^\#$
-closed and contains the parameter c, it contains
$J^\#$
-closed and contains the parameter c, it contains
![]() $L^{J^{\#}}(\mathbb {V},\tau ,c)$
as an inner model. Letting
$L^{J^{\#}}(\mathbb {V},\tau ,c)$
as an inner model. Letting
![]() $g\in L^{J^{\#}}[x]$
be generic such that
$g\in L^{J^{\#}}[x]$
be generic such that
![]() $\tau _g = x$
, we have that
$\tau _g = x$
, we have that
![]() $x\in L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. Using that
$x\in L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. Using that
![]() $J^\#$
determines itself on generic extensions and relativizes well, we can then reconstruct
$J^\#$
determines itself on generic extensions and relativizes well, we can then reconstruct
![]() $L^{J^{\#}}[x]$
inside
$L^{J^{\#}}[x]$
inside
![]() $L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. So the universe of
$L^{J^{\#}}(\mathbb {V},\tau ,a)[g]$
. So the universe of
![]() $\mathsf {HOD}^{L^{J^{\#}}[x]}_{a,x}$
and
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a,x}$
and
![]() $L^{J^{\#}}[x]$
are identical. The Vopenka forcing to add a real over
$L^{J^{\#}}[x]$
are identical. The Vopenka forcing to add a real over
![]() $\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is of size
$\mathsf {HOD}^{L^{J^{\#}}[x]}_{a}$
is of size
![]() $<\omega _1^V$
as
$<\omega _1^V$
as
![]() $\omega _1^V$
is inaccessible in
$\omega _1^V$
is inaccessible in
![]() $L^{J^{\#}}[x]$
.
$L^{J^{\#}}[x]$
.
By cheapo covering and the claim we can choose some
![]() $\lambda < \omega _1^V$
above the size of the forcing such that
$\lambda < \omega _1^V$
above the size of the forcing such that
Let
![]() $g\in V$
be
$g\in V$
be
![]() $Col(\omega ,\lambda )$
-generic over
$Col(\omega ,\lambda )$
-generic over
![]() $L^{J^{\#}}[x]$
and let
$L^{J^{\#}}[x]$
and let
![]() $y\in V$
be a real coding
$y\in V$
be a real coding
![]() $(g,x)$
. As J determines itself on generic extensions we have that
$(g,x)$
. As J determines itself on generic extensions we have that
![]() $L^{J^{\#}}[y] = L^{J^{\#}}[x][g]$
. Therefore,
$L^{J^{\#}}[y] = L^{J^{\#}}[x][g]$
. Therefore,
As
![]() $y\in \mathcal C$
we have that
$y\in \mathcal C$
we have that
We reach a contradiction if we can demonstrate the following claim:
Claim 5.3.
![]() $K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
$K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
Proof This claim is a verification that the proofs in Chapter 5 of CMIP [Reference Steel9] work given that J condenses well.
![]() $K^{ J}$
is still fully iterable inside
$K^{ J}$
is still fully iterable inside
![]() $L^{J^{\#}}[y]$
because it has no Woodin cardinals (above a) and J condenses well so its strategy is guided by
$L^{J^{\#}}[y]$
because it has no Woodin cardinals (above a) and J condenses well so its strategy is guided by
![]() $J^\#$
. This implies that
$J^\#$
. This implies that
![]() $K^{ J}$
is still the core model above a of
$K^{ J}$
is still the core model above a of
![]() $L^{J^{\#}}[y]$
, i.e., it is the common transitive collapse of
$L^{J^{\#}}[y]$
, i.e., it is the common transitive collapse of
![]() $Def(W,S)$
for any
$Def(W,S)$
for any
![]() $W,S$
such that W is an
$W,S$
such that W is an
![]() $\omega _1^V$
-iterable
$\omega _1^V$
-iterable
![]() $ J$
-weasel and
$ J$
-weasel and
![]() $\omega _1^V$
is S-thick. Using this characterization we can conclude that
$\omega _1^V$
is S-thick. Using this characterization we can conclude that
![]() $K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
$K^{ J}\in \mathsf {\mathsf {HOD}}^{L^{J^{\#}}[y]}_{a}$
.
Utilizing this theorem we wish to show
![]() $\forall \alpha \;W^*_\alpha $
. Suppose that for some fixed critical
$\forall \alpha \;W^*_\alpha $
. Suppose that for some fixed critical
![]() $\alpha $
,
$\alpha $
,
![]() $W_\alpha ^*$
holds, we wish to show that
$W_\alpha ^*$
holds, we wish to show that
![]() $W^*_{\alpha +1}$
holds. By the witness dichotomy (Theorem 3.6.1 of [Reference Schindler and Steel7]) this means that we need to see that for all
$W^*_{\alpha +1}$
holds. By the witness dichotomy (Theorem 3.6.1 of [Reference Schindler and Steel7]) this means that we need to see that for all
![]() $n<\omega $
,
$n<\omega $
,
![]() $J^n_\alpha $
is total on
$J^n_\alpha $
is total on
![]() $\mathbb {R}$
. Suppose that
$\mathbb {R}$
. Suppose that
![]() $\mathbb {R}$
is closed under
$\mathbb {R}$
is closed under
![]() $J = J^n_\alpha $
. To utilize Theorem 5.1 we first need to close
$J = J^n_\alpha $
. To utilize Theorem 5.1 we first need to close
![]() $\mathbb {R}$
under
$\mathbb {R}$
under
![]() $J^\#$
. As we’re assuming
$J^\#$
. As we’re assuming
![]() $\mathsf {DC}$
the Martin measure ultrapower is well-founded, so as J relativizes well we have that
$\mathsf {DC}$
the Martin measure ultrapower is well-founded, so as J relativizes well we have that
![]() $Ult(L^{J},\mu _{Tu}) = L^{J}$
and
$Ult(L^{J},\mu _{Tu}) = L^{J}$
and
![]() $J^\#$
exists (a full proof along these lines can be found in Theorem 28 of [Reference Steel and Zoble8]). One could avoid the use of
$J^\#$
exists (a full proof along these lines can be found in Theorem 28 of [Reference Steel and Zoble8]). One could avoid the use of
![]() $\mathsf {DC}$
by instead working inside
$\mathsf {DC}$
by instead working inside
![]() $\mathsf {HOD}^{L^{J}[x]}$
and utilizing the measurable cardinal on
$\mathsf {HOD}^{L^{J}[x]}$
and utilizing the measurable cardinal on
![]() $\omega _1^{L^{J}[x]}$
.
$\omega _1^{L^{J}[x]}$
.
Now we can show that
![]() $\mathbb {R}$
is closed under
$\mathbb {R}$
is closed under
![]() $J^{n+1}_\alpha $
. Let us fix
$J^{n+1}_\alpha $
. Let us fix
![]() $a\in \mathbb {R}$
. By Theorem 5.1, for any (hybrid) model operator J which relatives well and determines itself on generic extensions there is a cone of b on which
$a\in \mathbb {R}$
. By Theorem 5.1, for any (hybrid) model operator J which relatives well and determines itself on generic extensions there is a cone of b on which
cannot be
![]() $\omega _1^V+1$
iterable inside
$\omega _1^V+1$
iterable inside
![]() $\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. Let b lie in this cone, by applying the
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. Let b lie in this cone, by applying the
![]() $K^J$
existence dichotomy internal to
$K^J$
existence dichotomy internal to
![]() $\mathsf {HOD}_{a}^{L^{J^{\#}}[b]}$
we must have that the
$\mathsf {HOD}_{a}^{L^{J^{\#}}[b]}$
we must have that the
![]() $K^{c,J}(a)$
construction reaches
$K^{c,J}(a)$
construction reaches
![]() $M_1^{J,\#}(a)$
and
$M_1^{J,\#}(a)$
and
![]() $M_1^{J,\#}(a)$
is
$M_1^{J,\#}(a)$
is
![]() $\omega _1+1$
iterable in
$\omega _1+1$
iterable in
![]() $\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. In summary, we can define the following map on a cone:
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
. In summary, we can define the following map on a cone:
Consider the map
![]() $f:\mathcal D\to \mathbb {R}$
given by
$f:\mathcal D\to \mathbb {R}$
given by
By
![]() $\mathsf {\mathsf {TD}}$
, for each
$\mathsf {\mathsf {TD}}$
, for each
![]() $n<\omega $
the set
$n<\omega $
the set
![]() $\{b\in \mathbb {R} : n\in f([b])\}$
either contains a cone or is disjoint from a cone. Let
$\{b\in \mathbb {R} : n\in f([b])\}$
either contains a cone or is disjoint from a cone. Let
![]() $n\in \mathcal P$
iff
$n\in \mathcal P$
iff
![]() $n\in f([b])$
on a cone, then by countable choice for the reals
$n\in f([b])$
on a cone, then by countable choice for the reals
![]() $f([b]) = \mathcal {P}$
on a cone.
$f([b]) = \mathcal {P}$
on a cone.
One can see that
![]() $\mathcal P$
is
$\mathcal P$
is
![]() $\omega _1$
iterable in V: if
$\omega _1$
iterable in V: if
![]() $\mathcal T$
is a countable tree on
$\mathcal T$
is a countable tree on
![]() $\mathcal P$
of limit length, then the good branch through
$\mathcal P$
of limit length, then the good branch through
![]() $\mathcal T$
is the one picked by the strategies of
$\mathcal T$
is the one picked by the strategies of
![]() $\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
on a cone. Turing determinacy allows us to extend this to an
$\mathsf {\mathsf {HOD}}_{a}^{L^{J^{\#}}[b]}$
on a cone. Turing determinacy allows us to extend this to an
![]() $\omega _1+1$
-iteration strategy using the measurability of
$\omega _1+1$
-iteration strategy using the measurability of
![]() $\omega _1$
; therefore,
$\omega _1$
; therefore,
![]() $\mathcal P$
is the actual
$\mathcal P$
is the actual
![]() $M_1^{J,\#}(a)$
. From this, the map
$M_1^{J,\#}(a)$
. From this, the map
![]() $a\mapsto J^{n+1}_\alpha (a) := M_1^{J,\#}(a)$
can be defined.
$a\mapsto J^{n+1}_\alpha (a) := M_1^{J,\#}(a)$
can be defined.
Note 5.4. Given a model operator J, in The Core Model Induction [Reference Schindler and Steel7] the operators
![]() $J^{n}$
are defined as
$J^{n}$
are defined as
![]() $M^{J,\#}_n$
. This is not literally equal but intertranslatable with the hierarchy where
$M^{J,\#}_n$
. This is not literally equal but intertranslatable with the hierarchy where
![]() $J^{n+1} = M^{J^n,\#}_1$
as utilized above.
$J^{n+1} = M^{J^n,\#}_1$
as utilized above.
Note 5.5. The strongest choice principle necessary in the above argument is
![]() $\mathsf {CC}_{\mathbb {R}}$
(which follows from
$\mathsf {CC}_{\mathbb {R}}$
(which follows from
![]() $\mathsf {TD}$
[Reference Peng and Yu6]); however, the assumption
$\mathsf {TD}$
[Reference Peng and Yu6]); however, the assumption
![]() $L(\mathbb {R})\models \mathsf {\mathsf {DC}}$
seems to be necessary for the guts of the core model induction. In particular, it’s used in both the Kechris–Woodin transfer theorem and in the A-iterability proof.
$L(\mathbb {R})\models \mathsf {\mathsf {DC}}$
seems to be necessary for the guts of the core model induction. In particular, it’s used in both the Kechris–Woodin transfer theorem and in the A-iterability proof.
Acknowledgements
The author would like to thank Woodin for giving permission to write up this result. He would also like to thank Schindler and Steel for reading over the proof and giving several helpful suggestions.