Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T11:33:44.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone reducibility and the family of infinite sets

Published online by Cambridge University Press:  12 March 2014

Douglas Cenzer
Douglas Cenzer*
Affiliation:
University of Florida, Gainesville, Florida 32611
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A and B be subsets of the space 2N of sets of natural numbers. A is said to be Wadge reducible to B if there is a continuous map Φ from 2N into 2N such that A = Φ−1 (B); A is said to be monotone reducible to B if in addition the map Φ is monotone, that is, a ⊂ b implies Φ(a) ⊂ Φ(b). The set A is said to be monotone if a ∈ A and a ⊂ b imply b ∈ A. For monotone sets, it is shown that, as for Wadge reducibility, sets low in the arithmetical hierarchy are nicely ordered. The 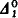sets are all reducible to the ( 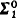but not 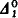) sets, which are in turn all reducible to the strictly 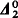sets, which are all in turn reducible to the strictly 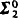sets. In addition, the nontrivial 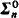sets all have the same degree for n ≤ 2. For Wadge reducibility, these results extend throughout the Borel hierarchy. In contrast, we give two natural strictly 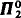monotone sets which have different monotone degrees. We show that every 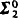monotone set is actually 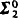positive. We also consider reducibility for subsets of the space of compact subsets of 2N. This leads to the result that the finitely iterated Cantor-Bendixson derivative Dn is a Borel map of class exactly 2n, which answers a question of Kuratowski.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 774 - 782
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cenzer, D. and Mauldin, R. D., On the Borel class of the derived set operator, Bulletin de la Société Mathématique de France, vol. 110 (1982), pp. 357–380.CrossRefGoogle Scholar
[2]Kuratowski, K., Some problems concerning semi-continuous set-valued mappings, Set-valued mappings, selections and topological properties of 2x (Proceedings of a conference, Buffalo, New York, 1969), Lecture Notes in Mathematics, vol. 171, Springer-Verlag, Berlin, 1970, pp. 45–48.CrossRefGoogle Scholar
[3]Lusin, N., Leçons sur les ensembles analytiques, Gauthier-Villars, Paris, 1930.Google Scholar
[4]Martin, D. A., Borel determinacy, Annals of Mathematics, ser. 2, vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
[5]Steel, J., Determinateness and subsystems of analysis, Ph.D. Thesis, University of California, Berkeley, California, 1976.Google Scholar
[6]Van Wesep, R., Wadge degrees and descriptive set theory, Cabal seminar 76–77, Lecture Notes in Mathematics, vol. 689, Springer-Verlag, Berlin, 1978, pp. 151–170.CrossRefGoogle Scholar