Published online by Cambridge University Press: 12 March 2014
Several results in the theory of recursion in higher types indicate that the effect of a higher type functional on the lower types does not reflect the high type, i.e. the same effect could be obtained by functionals of relatively low type. The two main results here are:
Plus -1 - Theorem (G. Sacks [6] for k = 1, [7] for k > 1). Let H be a normal functional of type ≥ k + 1. Then there exists a normal functional F of type k + 1 such that k-sc(F) = k-sc(H), i.e. the same subsets of tp(k − 1) are recursive in F and H.
Plus - 2 - Theorem (L. Harrington [1]). Let H be a normal functional of type ≥ k + 2. Then there exists a normal functional F of type k +2 such that k-en(H) = k-en(F), i.e. the same subsets of tp(k − 1) are semirecursive in F and H.
The results in this paper also indicate that higher types cannot have too much influence on lower types. The key is the Skolem-Löwenheim theorem. Among the results we mention:
(1) Let n < m. A ⊆ tp(n) × tp(m) be Kleene-semicomputable. Let x ∈ B ⇔ ∀y∈tp(m), ⟨x, y⟩ ∈ A. Then B is 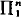 . This result may be relativized to a functional of type n + 1.
. This result may be relativized to a functional of type n + 1.
(2) Let k0 be the type-k-functional that is constant zero. Let F be a functional of type < k. Then, for i ≤ k −2, i-sc(F ,k0) = i-sc(F), i-en(F, k0) = ∀tp(i)(i-en(F)).