Article contents
Minimum models of analysis1
Published online by Cambridge University Press: 12 March 2014
Extract
Although there is no smallest ω model [6], Putnam and Gandy independently proved about 1963 that the class of ramified analytical sets, as defined by Cohen [3], form the smallest β model of analysis [2], [8]. This paper will consider other restricted classes of models, namely the βn models for integers n > 1 [10], and prove under appropriate assumptions the existence of minimum such models. In fact we shall construct the minimum βn model in a fashion similar to the procedure yielding the class of ramified analytical sets, but adding at each stage a segment of the sets 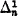 in those already obtained (for n a fixed integer > 1).
in those already obtained (for n a fixed integer > 1).
Roughly speaking a βn model is an ω model absolute for n-set-quantifier assertions about its subsets of natural numbers. A β model is simply a β1 model. See Enderton and Friedman [4] for a further investigation of βn models.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
Footnotes
This paper presents the work of the author's doctoral dissertation submitted to the University of California at Berkeley in February 1969.
References
BIBLIOGRAPHY
- 3
- Cited by


