Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T13:24:27.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal readability of intuitionistic arithmetic and elementary analysis

Published online by Cambridge University Press:  12 March 2014

Zlatan Damnjanovic
Zlatan Damnjanovic*
Affiliation:
School of Philosophy, University of Southern California, Los Angeles, California 90089–0451
Get access Rights & Permissions [Opens in a new window]

Abstract

A new method of “minimal” readability is proposed and applied to show that the definable functions of Heyting arithmetic (HA)—functions f such that HA ⊢ ∀x∃!yA(x, y) ⇒ for all m, A(m, f(m)) is true, where A(x, y) may be an arbitrary formula of ℒ(HA) with only x,y free—are precisely the provably recursive functions of the classical Peano arithmetic (PA), i.e., the < ε0-recursive functions. It is proved that, for prenex sentences provable in HA, Skolem functions may always be chosen to be < ε0-recursive. The method is extended to intuitionistic finite-type arithmetic, 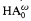, and elementary analysis. Generalized forms of Kreisel's characterization of the provably recursive functions of PA and of the no-counterexample-interpretation for PA are consequently derived.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 4 , December 1995 , pp. 1208 - 1241
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buchholz, W. and Wainer, S. S., Provably computable functions and the fast growing hierarchy, Logic and Combinatorics (Simpson, S., editor), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, Rhode Island, 1987, pp. 179–198.CrossRefGoogle Scholar
[2]Damnjanovic, Z., Elementary readability, Journal of Philosophical Logic (to appear).Google Scholar
[3]Damnjanovic, Z., Strictly primitive recursive realizability. I, this Journal, vol. 59 (1994), pp. 1210–1227.Google Scholar
[4]Gödel, K., “Über eine bisher noch nicht benützte Erweiterung des finites Standpunktes”, Diabetica, vol. 12 (1958), pp. 280–287; reprinted, with English translation, in his Collected works. Vol. II (1990), Oxford University Press, Oxford.Google Scholar
[5]Goodman, N. D., The theory of the Gödel functionals, this Journal, vol. 41 (1976), pp. 574–582.Google Scholar
[6]Ketonen, J. and Solovay, R. M., Rapidly growing Ramsey functions, Annals of Mathematics ser. 2, vol. 113 (1981), pp. 267–314.CrossRefGoogle Scholar
[7]Kleene, S. C., Introduction to metamathematics, Van Nostrand, New York, 1952.Google Scholar
[8]Kleene, S. C., Extension of an effectively generated class of functions by enumeration, Colloquium Mathematicum, vol. 6 (1958), pp. 67–78.CrossRefGoogle Scholar
[9]Kleene, S. C., Realizability: a retrospective survey, Cambridge summer school in mathematical logic (Mathias, A. R. D. and Rogers, H., editors), Springer-Verlag, Berlin, 1973, pp. 95–112.CrossRefGoogle Scholar
[10]Kreisel, G., On the interpretation of non-finitist proofs. I, II, this Journal, vol. 16 (1951), pp. 241–267; vol. 17 (1952), pp. 43–58.Google Scholar
[11]Kreisel, G., Mathematical significance of consistency proofs, this Journal, vol. 23 (1958), pp. 155–182.Google Scholar
[12]Kreisel, G., The non-derivability of ¬(x)A(x) → (Ex)¬A(x), A primitive recursive, in intuitionistic formal systems (abstract), this Journal, vol. 23 (1958), pp. 456–457.Google Scholar
[13]Kripke, S. A., Semantical analysis of intuitionistic logic. I, Formal systems and recursive functions (Crossley, J. N. and Dummett, M. E., editors), North-Holland, Amsterdam, 1965, pp. 92–130.CrossRefGoogle Scholar
[14]Leivant, D., Syntactic translations and provably recursive functions, this Journal, vol. 50 (1985), pp. 682–688.Google Scholar
[15]Rose, H. E., Subrecursion: functions and hierarchies, Clarendon Press, Oxford, 1984.Google Scholar
[16]Schwichtenberg, H., Elimination of higher type levels in definitions of primitive recursive functionals by means of transfinite recursion, Logic Colloquium '73 (Rose, H. E. and Shepherdson, J. C., editors), North-Holland, Amsterdam, 1975, pp. 280–303.Google Scholar
[17]Schwichtenberg, H., Proof theory: Some applications of cut-elimination, Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 867–895.CrossRefGoogle Scholar
[18]Shoenfield, J. R., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[19]Tait, W. W., Nested recursion, Mathematische Annalen, vol. 143 (1961), pp. 236–250.CrossRefGoogle Scholar
[20]Tait, W. W., Infinitely long terms of transfinite type. I, Formal systems and recursive functions (Crossley, J. N. and Dummett, M. E., editors), North-Holland, Amsterdam, 1965, pp. 176–185.CrossRefGoogle Scholar
[21]Troelstra, A. S. (editor), Metamathematical investigations of intuitionistic arithmetic and analysis, Springer-Verlag, Berlin, 1973.CrossRefGoogle Scholar
[22]Troelstra, A. S., Constructivism in mathematics: an introduction, Vols. 1, 2, North-Holland, Amsterdam, 1988.Google Scholar
[23]Troelstra, A. S., Introductory note to [4], in Kurt Gödel, Collected works, Vol. II, Oxford University Press, Oxford, 1990, pp. 217–241.Google Scholar
[24]Wainer, S. S., A classification of the ordinal recursive functions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 13 (1970), pp. 136–153.CrossRefGoogle Scholar
[25]Wainer, S. S., Ordinal recursion and a refinement of the extended Grzegorczyk hierarchy, this Journal, vol. 37 (1972), pp. 281–292.Google Scholar