No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Takeuti [6] has suggested the need for higher axioms for set theory which are analogous to higher axioms of infinity, but which claim that power sets are in some sense large. In this paper we investigate a reflection axiom of this sort (Axiom T).
In §1, we introduce Axiom T and explore some related axioms. A technical lemma involving an elementary embedding is developed in §2 which allows us, in §3, to prove the relative consistency of Axiom T.
The reader is assumed to be familiar with ramified forcing languages and the usual techniques of forcing. A suitable treatment of these subjects is given by Takeuti and Zaring [7].
ZFC, GBC, ZF and GB are the set theories of Zermelo-Fraenkel and of Gödel-Bernays, with and without the axiom of choice (AC). CH is the continuum hypothesis.
For α an ordinal, define
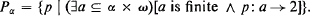
For p1, p2 ∈ pα let p1 ≤ p2 mean that p1 ⊇ p2 (thus p1 is the stronger forcing condition). It is well known that Pα satisfies the countable chain condition [5].