Article contents
Hierarchies of forcing axioms II
Published online by Cambridge University Press: 12 March 2014
Abstract
A 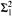 truth for λ is a pair 〈Q, ψ〉 so that Q ⊆ Hλ, ψ is a first order formula with one free variable, and there exists B ⊆ Hλ+ such that (Hλ+; ∈, B) ⊨ ψ[Q]. A cardinal λ is
truth for λ is a pair 〈Q, ψ〉 so that Q ⊆ Hλ, ψ is a first order formula with one free variable, and there exists B ⊆ Hλ+ such that (Hλ+; ∈, B) ⊨ ψ[Q]. A cardinal λ is 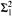 , indescribable just in case that for every
, indescribable just in case that for every 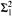 truth 〈Q, ψ〈 for λ, there exists
truth 〈Q, ψ〈 for λ, there exists 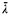 < λ so that
< λ so that 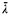 is a cardinal and 〈Q ∩
is a cardinal and 〈Q ∩ 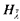 , ψ) is a
, ψ) is a 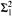 truth for
truth for 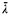 . More generally, an interval of cardinals [κ, λ] with κ ≤ λ is
. More generally, an interval of cardinals [κ, λ] with κ ≤ λ is 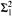 indescribable if for every
indescribable if for every 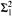 truth 〈Q, ψ〈 for λ, there exists
truth 〈Q, ψ〈 for λ, there exists 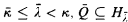 , and π:
, and π: 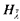 → Hλ so that
→ Hλ so that 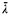 is a cardinal,
is a cardinal, 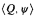 is a
is a 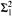 truth for
truth for 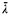 , and π is elementary from (
, and π is elementary from (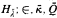 ) into (H; ∈, κ, Q) with
) into (H; ∈, κ, Q) with 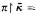 id.
id.
We prove that the restriction of the proper forcing axiom to ϲ-linked posets requires a 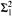 indescribable cardinal in L, and that the restriction of the proper forcing axiom to ϲ+-linked posets, in a proper forcing extension of a fine structural model, requires a
indescribable cardinal in L, and that the restriction of the proper forcing axiom to ϲ+-linked posets, in a proper forcing extension of a fine structural model, requires a 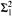 indescribable 1-gap [κ, κ+]. These results show that the respective forward directions obtained in Hierarchies of Forcing Axioms I by Neeman and Schimmerling are optimal.
indescribable 1-gap [κ, κ+]. These results show that the respective forward directions obtained in Hierarchies of Forcing Axioms I by Neeman and Schimmerling are optimal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 5
- Cited by


