Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T10:40:40.150Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPOIDS AND RELATIVE INTERNALITY

Published online by Cambridge University Press:  23 April 2019

LÉO JIMENEZ
LÉO JIMENEZ*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME 255 HURLEY NOTRE DAME, IN46556, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In a stable theory, a stationary type 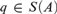$q \in S\left( A \right)$ internal to a family of partial types 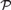${\cal P}$ over A gives rise to a type-definable group, called its binding group. This group is isomorphic to the group $Aut\left( {q/{\cal P},A} \right)$ of permutations of the set of realizations of q, induced by automorphisms of the monster model, fixing 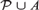${\cal P}\,\mathop \cup \nolimits \,A$ pointwise. In this article, we investigate families of internal types varying uniformly, what we will call relative internality. We prove that the binding groups also vary uniformly, and are the isotropy groups of a natural type-definable groupoid (and even more). We then investigate how properties of this groupoid are related to properties of the type. In particular, we obtain internality criteria for certain 2-analysable types, and a sufficient condition for a type to preserve internality.

Keywords

03C4503C95stability theoryinternalitybinding groupgroupoid
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 987 - 1006
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chatzidakis, Z., A note on canonical bases and one-based types in supersimple theories. Confluentes Mathematici, vol. 4 (2012), no. 03, p. 1250004.Google Scholar
Chatzidakis, Z., Harrison-Trainor, M., and Moosa, R., Differential-algebraic jet spaces preserve internality to the constants, this Journal, vol. 80 (2015), no. 3, pp. 1022–1034.Google Scholar
Friedman, G., Survey article: An elementary illustrated introduction to simplicial sets. The Rocky Mountain Journal of Mathematics, vol. 42 (2012), pp. 353–423.Google Scholar
Goodrick, J. and Kolesnikov, A., Groupoids, covers, and 3-uniqueness in stable theories, this Journal, vol. 75 (2010), no. 3, pp. 905–929.Google Scholar
Haykazyan, L. and Moosa, R., Functoriality and uniformity in Hrushovski’s groupoid-cover correspondence. Annals of Pure and Applied Logic, vol. 169 (2018), no. 8, pp. 705–730.Google Scholar
Hrushovski, E., Groupoids, imaginaries and internal covers. Turkish Journal of Mathematics, vol. 36 (2012), no. 2, pp. 173–198.Google Scholar
Moosa, R., A model-theoretic counterpart to Moishezon morphisms, Models, Logics, and Higher-Dimensional Categories: A Tribute to the Work of Mihály Makkai (Hart, B., Kucera, T. G., Pillay, A., Scott, P. J., and Seely, R. A. G., editors), CRM Proceedings and Lecture Notes, vol. 53, American Mathematical Society, Providence, RI, 2010, pp. 177–188.Google Scholar
Pillay, A., Geometric Stability Theory, vol. 32, Oxford University Press, New York, 1996.Google Scholar
Pillay, A., Remarks on a theorem of Campana and Fujiki. Fundamenta Mathematicae, vol. 174 (2002), pp. 187–192.Google Scholar
Pillay, A. and Ziegler, M., Jet spaces of varieties over differential and difference fields. Selecta Mathematica, vol. 9 (2003), no. 4, pp. 579–599.Google Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, vol. 40, Cambridge University Press, New York, 2012.Google Scholar